概率质量函数(Probability Mass Function)和期望课程笔记

Posted 2023-02-20 Xurtle

随机变量的数学定义

从样本空间到实数值的映射函数。

---

一个样本空间可以定义多个随机变量

一个或几个随机变量的函数构成一个新的随机变量

---

概率质量函数的定义

$p_X(x) = P(X = x) = P(\\\\omega \\in \\Omega \\ s.t. X(\\omega) = x\\)$

上面公式的含义为在随机变量X的映射函数下，所有样本空间中的结果在此映射下输出结果为x的概率。

属性如下：

1. $p_X(x) \\ge 0$
2. $\\sum_xp_X(x) = 1$

Bernoulli和指示器随机变量

Bernoulli随机变量定义：

$X = \\begincases 1, & \\textw.p.(with probability) p \\\\ 0, & \\textw.p.(with probability) 1 - p \\endcases$

参数p的取值为：$p \\in [0, 1]$

$P_X(0) = 1 - p$
$P_X(1) = p$

它适合对结果只有成功或失败、正面或背面、等等来进行建模。

指示器随机变量定义：

事件A的指示器随机变量：$I_A = 1 当且仅当(iff) A 发生$

因此：$P_I_A(1) = P(I_A = 1) = P(A)$

指示器随机变量是非常有用的，因为它把对事件的操作转换成了对随机变量的操作。有时，对随机变量计算比对事件更加容易。

离散均匀随机变量

例子如下：

二项随机变量

例子如下：

二项随机变量的PMF图像如下：

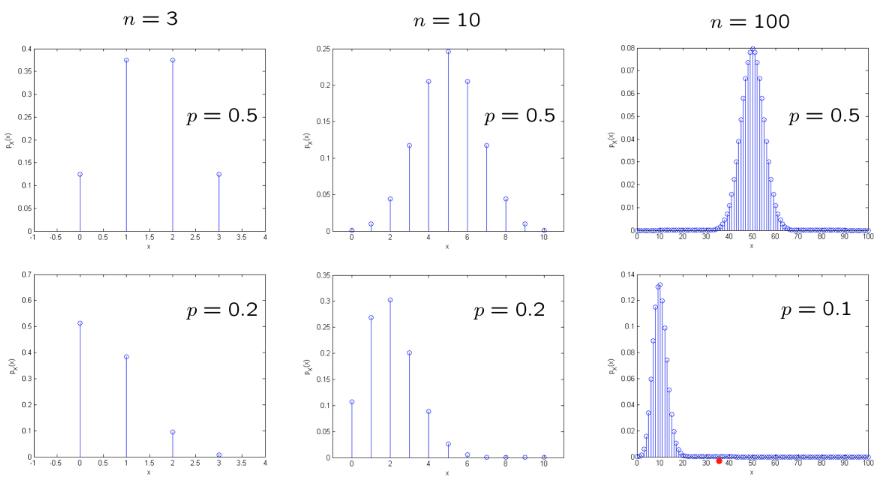
几何随机变量

例子如下：

随机变量的期望值/平均值

定义：$E[X] = \\sum\\limits_xxP_X(x)$

上面的定义可以解释成大量独立实验的平均值。

注意：如果我们有无穷的求和项，那么我们需要将此式定义明确。所以，我们假设$\\sum\\limits_x|x|P_X(x) \\lt \\infty$

Bernoulli和指示器随机变量的期望值

$X = \\begincases 1, & \\textw.p.(with probability) p \\\\ 0, & \\textw.p.(with probability) 1 - p \\endcases$

E[X] = 1 * p + 0 * (1 - p) = p

指示器随机变量的期望值:

$E[I_A] = P(A)$

均匀随机变量的期望值

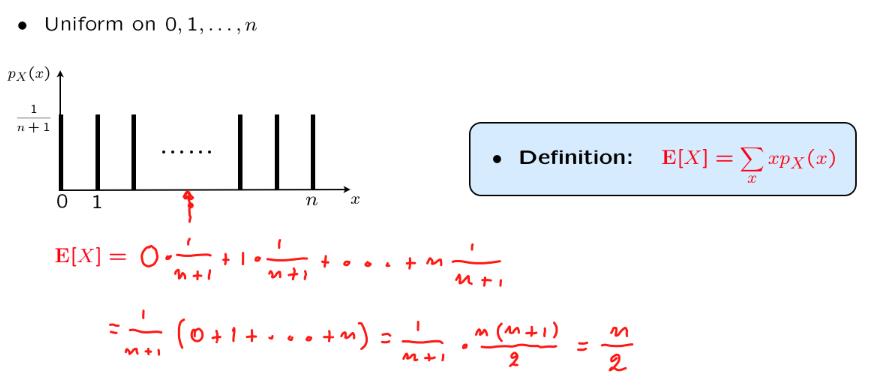
期望的基本属性

用于计算E[g(X)]的期望值规则

设X为随机变量，令Y = g(X).

则$E[Y] = E[g(X)] = \\sum\\limits_xg(x)p_X(x)$

注意：通常情况下，$E[g(X)] \\neq g(E[X])$

期望的线性

E[aX + b] = aE[X] + b.

基于期望值规则的推导：

令g(x) = ax + b.

E[g(x)] = E[ax + b] = $\\sum\\limits_x(ax + b)P_X(x) = a\\sum\\limits_xxP_X(x) + b\\sum\\limits_xP_X(x) = aE[x] + b$

在这个例子中，E[g(x)] = g(E[x])。当g(x)是线性函数时，这个等式成立。当其为非线性函数时，通常情况下是不成立的。