2022-04-25:给定一个整数数组,返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。 输入: nums = [1,3,1] k = 1 输出:
Posted 福大大架构师每日一题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022-04-25:给定一个整数数组,返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。 输入: nums = [1,3,1] k = 1 输出:相关的知识,希望对你有一定的参考价值。
2022-04-25:给定一个整数数组,返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。
输入:
nums = [1,3,1]
k = 1
输出:0
解释:
所有数对如下:
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
因此第 1 个最小距离的数对是 (1,1),它们之间的距离为 0。
力扣719. 找出第 k 小的距离对。
答案2022-04-25:
排序。二分法,f(x)是小于等于x的个数。刚刚大于等于k的。
f(x)不回退窗口。
时间复杂度:O(N*logN)+O(log(max-min)*N)。
代码用rust编写。代码如下:
fn main()
let mut nums: Vec<isize> = vec![1, 3, 2];
let k: isize = 1;
let ans = smallest_distance_pair(&mut nums, k);
println!("ans = ", ans);
fn smallest_distance_pair(nums: &mut Vec<isize>, k: isize) -> isize
let n: isize = nums.len() as isize;
nums.sort_by(|a, b| a.cmp(&b));
let mut l: isize = 0;
let mut r: isize = nums[(n - 1) as usize] - nums[0];
let mut ans: isize = 0;
while l <= r
let dis: isize = l + ((r - l) >> 1);
let cnt: isize = f(nums, dis);
if cnt >= k
ans = dis;
r = dis - 1;
else
l = dis + 1;
return ans;
// <= dis的数字对,有几个,返回
fn f(arr: &mut Vec<isize>, dis: isize) -> isize
let mut cnt: isize = 0;
let mut l: isize = 0;
let mut r: isize = 0;
while l < arr.len() as isize
while r < arr.len() as isize && arr[r as usize] <= arr[l as usize] + dis
r += 1;
cnt += r - l - 1;
l += 1;
return cnt;
执行结果如下:
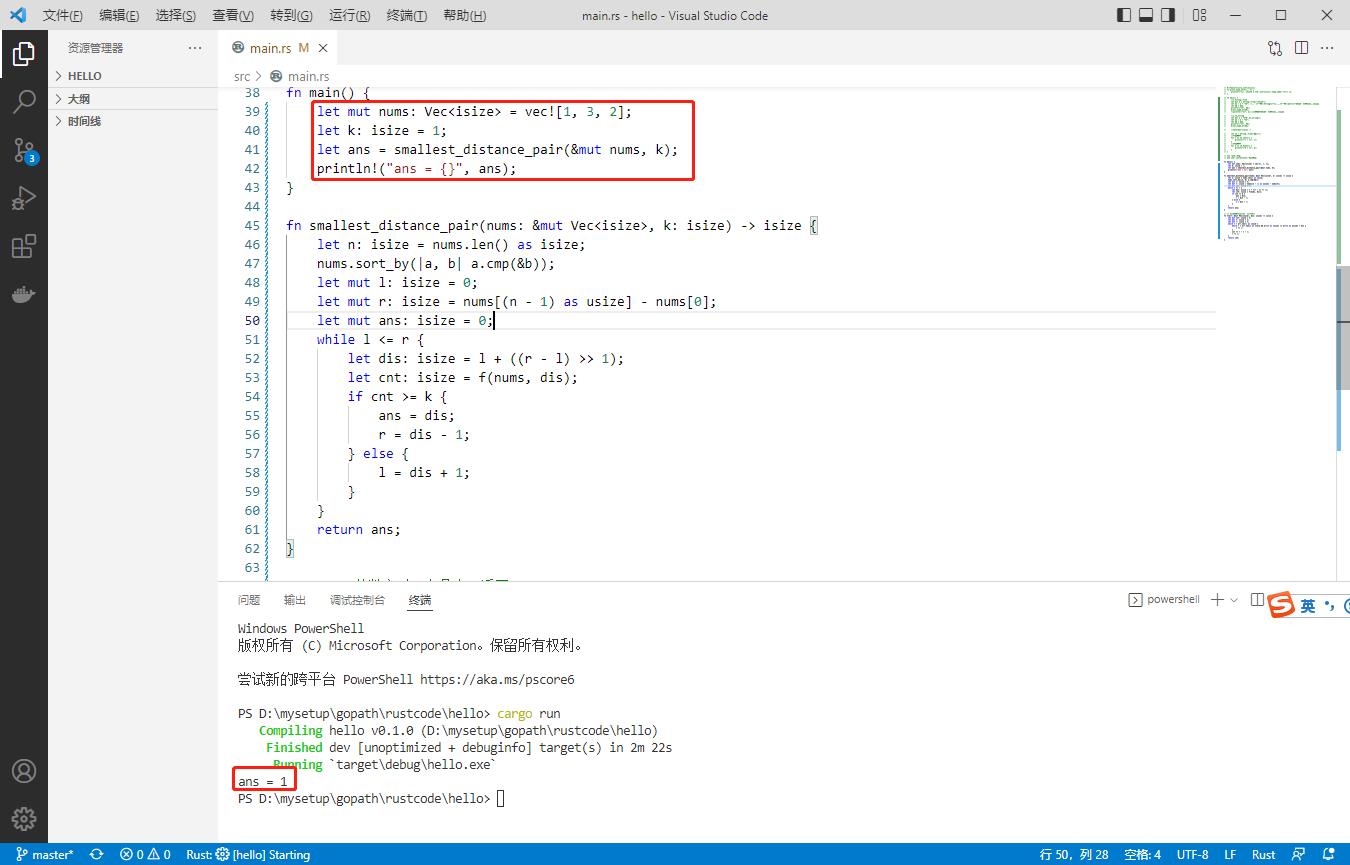
以上是关于2022-04-25:给定一个整数数组,返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。 输入: nums = [1,3,1] k = 1 输出:的主要内容,如果未能解决你的问题,请参考以下文章