[机器学习与scikit-learn-51]:模型评估-图解回归模型的评估指标MSEMAERMSER2RSS与代码示例
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-51]:模型评估-图解回归模型的评估指标MSEMAERMSER2RSS与代码示例相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/124413449
目录
第2章 平均绝对误差(mean absolute error, MAE)- L1损失
第3章 残差的平方和RSS (Residual Square Summary)
第4章 均方误差MSE(Mean平均 Square Error) - L2损失
第7章 总离差平方和TSS(Total of Summary Square)
第8章 决定系数R^2(Coefficient of Determination)
9.6 关于scikit-learn 交叉验证时,MSE为负数的说明
前言:
本文探讨回归模型的评估指标。
第1章 残差residual error
1.1 残差的定义
“残差”蕴含了有关模型基本假设的重要信息。
如果回归模型正确的话, 我们可以将残差看作误差的观测值(不是理论值)。
利用残差所提供的信息,来考察模型假设的合理性及数据的可靠性称为残差分析。
1.2 残差的数学表达式
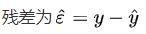
1.3 残差计算的几何图形
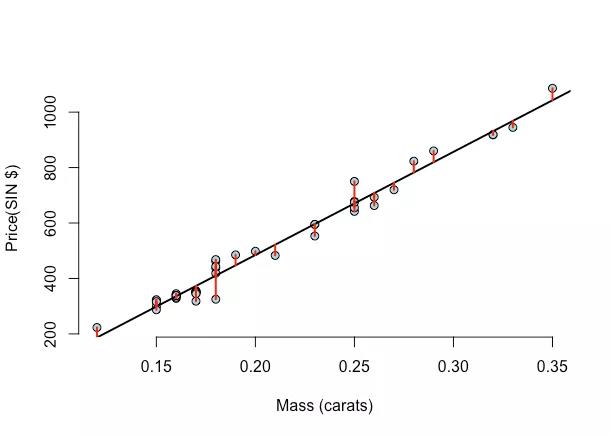
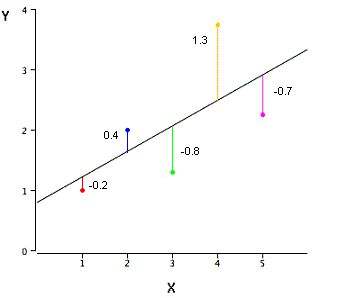
1.4 残差数值的几何图形
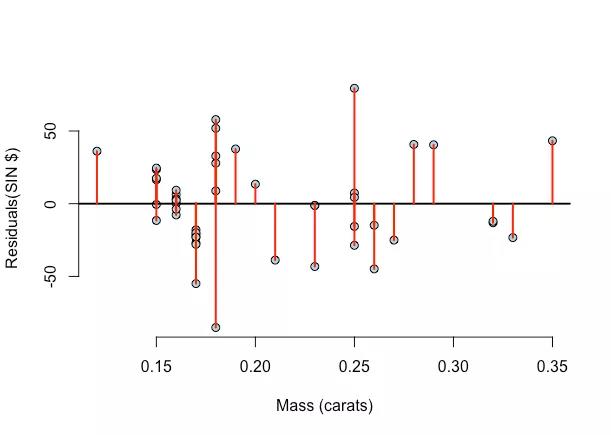
残差值,残差是有符号的,可正可负。因此,残差的累计和接近0.
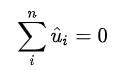
这就要求残差图满足就代表每个残差不相关(独立性),分布满足正态性。
分布的正态性往往等同于随机。
1.5 残差分析
残差分析(residual analysis)就是通过残差所提供的信息(残留信息),分析出数据的可靠性、周期性或其它干扰,用于分析模型的假定正确与否的方法。
在回归分析中,测定值与按回归方程预测的值之差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。δ*遵从标准正态分布N(0,1)。
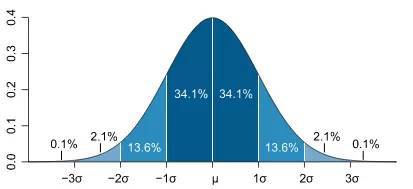
实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合。
显然,有多少对数据,就有多少个残差。残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。
残差图的分布趋势可以帮助判明所拟合的线性模型是否满足有关假设。如残差是否近似正态分布、是否方差齐次,变量间是否有其它非线性关系及是否还有重要自变量未进入模型等。.当判明有某种假设条件欠缺时, 进一步的问题就是加以校正或补救。
1.6 残差的意义:
残差的重要意义:
看残差是否符合正态分布。
但残差累计和为0,并不能完全反应模型性能的好坏,只能反应拟合曲线正好落在样本点的中心。
为了进一步反应拟合效果,需要进一步的指标。
第2章 平均绝对误差(mean absolute error, MAE)- L1损失
2.1 概述
MAE是目标值和预测值之差的绝对值之和,即每个残差值的绝对值之和。
其只衡量了预测值误差之和的平均,而不考虑方向,取值范围也是从0到正无穷。
2.2 MAE的数学表达式
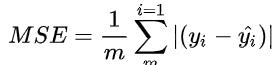
2.3 MAE误差的几何含义
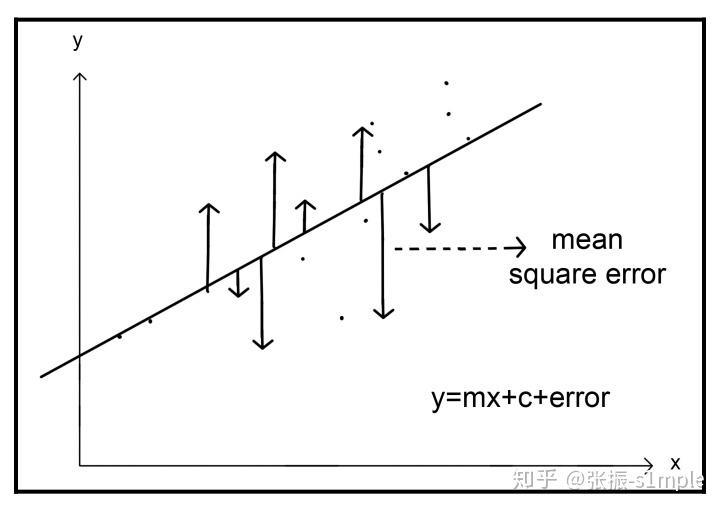
2.4 MAE的函数图形(红色图像)
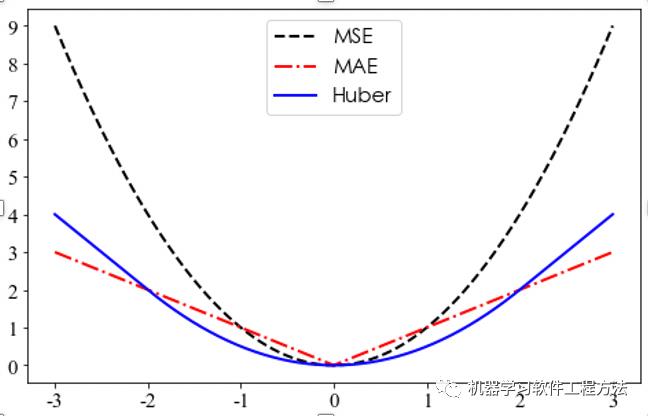
2.5 代码演示
from sklearn.metrics import mean_absolute_error
第3章 残差的平方和RSS (Residual Square Summary)
3.1 残差平方和的定义
把每个残差平方之后加起来 称为残差平方和(残差面积和)(相当于实际值与预测值之间差的平方之和)。
3.2 残差平方和的数学表达
RSS = ∑(u)2称为残差平方和。
3.3 残差平方和的意义
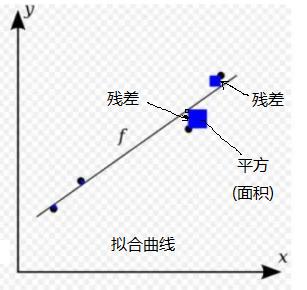
它表示随机误差的效果
“残差和”RSS反应了:未拟合出来的信息总量的大小
(1)残差RSS越大,未拟合出来的信息总量越大,拟合效果越差。
(1)残差RSS越大,未拟合出来的信息总量越大,拟合效果越好。
3.4 RSS的缺点
(1)RSS指标与样本的个数相关,模型不变的情形下,样本个数越多,RSS越大,样本个数越少,RSS值越小。
因此,需要一种指标,能够消除样本个数带来的影响,这就是MSE.
第4章 均方误差MSE(Mean平均 Square Error) - L2损失
4.1 什么是均分误差
均方误差(MSE)是最常用的回归损失函数,计算方法是求预测值与真实值之间距离的平方和,再求平均。
对比平均绝对误差,均方误差对异常值更敏感,因为均分误差对误差进行了放大(乘方)。
4.2 数学公式
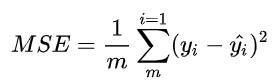
4.3 几何意义

4.4 几何图形(黑色图形)

4.5 代码演示
4.6 MSE的缺点
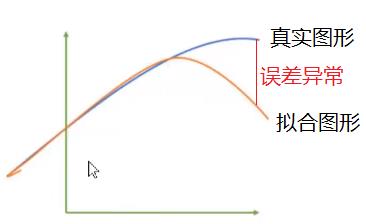
(1)MSE是平方和,放大了残差的差易 =》 对应策略:均分根误差
(2)无法发现异常点:=》应对策略: R2决定系数
MSE是所有样本残差平方求和之后的平均值,这就导致在局部的异常点,如上图红色部分,会被淹没在平均值中,样本个数越大, 则N越大,异常点处的误差,就会被平均后的值越小,越无法发现拟合曲线中的异常部分。
(3)MSE没有上界:=》应对策略: R2决定系数
不同模型之间的MSE没有可比性。
第5章 均方根误差(RMSE)
5.1 什么是均方根误差
均方根误差是均分误差开根号。
5.2 数学公式
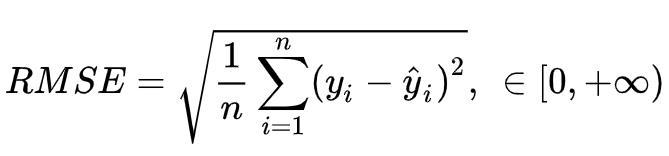
5.3 几何意义
同上
5.4 几何图形
同上
第6章 方差
6.1 什么是方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
6.2 方差的数学公式
方差用来计算每一个变量(观察值)与总体均数之间的差异。
为避免出现离均差总和为零,统计学采用方差的平方和来描述变量的变异程度。总体方差计算公式:

6.3 方差的几何图形
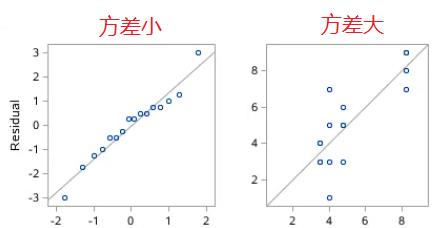
6.4 方差的意义
方差反应了数值的波动范围,方差越大,波动范围越大,如果方差位0,则表示没有波动,所有数值都相等。
另一方面,方差反应的是其所携带的信息量的大小:
- 方差越大,说明波动范围越大,不确定性越大,数据所携带的信息平均量越大。
- 方差越小,说明波动范围越小,不确定性越小,数据所携带的信息平均量越小。
6.5 标准方差
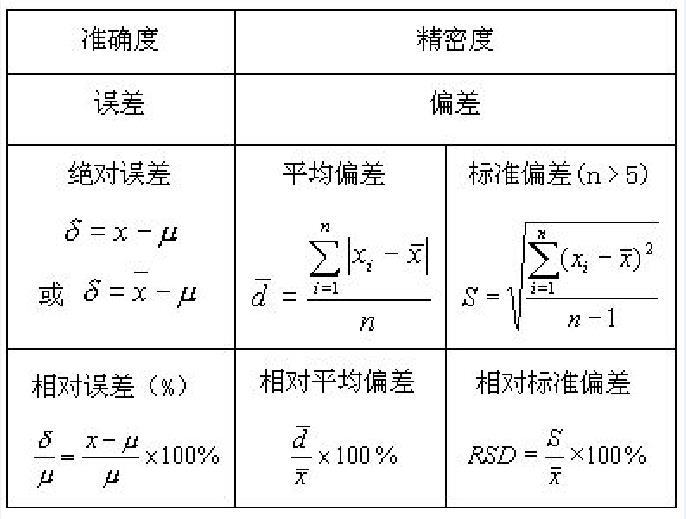
第7章 总离差平方和TSS(Total of Summary Square)
7.1 什么是离差/平均差deviation
方差是样本数据与均值差的平方和,再求平均。
其中样本数据预均值的差,我们给它取一个专门的名字,称为“离差”或平均差。
7.2 总离差平方和TSS
所有样本的离差的平方之后的累计和,称为总离差平方和TSS。
TSS与方差的唯一区别就是,方差进行了平均,TSS没有平均。
7.3 总离差平方和TSS的数学公式
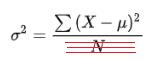
7.4 TSS的含义
- TSS越大,说明波动范围越大,不确定性越大,数据所携带的信息总量越大。
- TSS越小,说明波动范围越小,不确定性越小,数据所携带的信息总量越小。
第8章 决定系数R^2(Coefficient of Determination)
8.1 均分误差MSE的缺点
均分误差是一个非常简单有效的评估拟合效果的评估指标。

但MSE有2个缺点:
(1)隐藏了异常残差,异常残差被平均后,会被淹没在平均值中,在MSE中无法反应。
(2)MSE是一个绝对值,没有上限,不同模型之间无法比较。
为了克服上述缺点,引入了决定系数,它克服了上述两个缺点。
8.2 什么是决定系数R^2
这是一个比较难理解的参数,但有了前面的铺垫,就比如容易理解。
它反应了拟合模型模型对样本数据的拟合程度,是一个相对值,如90%的拟合程度。
8.3 决定系数的计算方法
(1)残差的平方和RSS (Residual Square Summary)
“残差和”RSS反应了:未拟合出来的信息总量的大小
- 残差RSS越大,未拟合出来的信息总量越大,拟合效果越差。
- 残差RSS越大,未拟合出来的信息总量越大,拟合效果越好。
(2)离差平方和TSS
离差平方和TSS反应了:样本数据中总信息总量的大小
- TSS越大,说明波动范围越大,不确定性越大,数据所携带的信息总量越大。
- TSS越小,说明波动范围越小,不确定性越小,数据所携带的信息总量越小。
(3)RSS/TSS = 未拟合出来的信息总量/数据所携带的信息总量越大
RSS/TSS是一个比值,它是未拟合出来的信息总量与样本数据中自身携带的信息总量的比值,它反应了模型未拟合出来的信息的比率。
(4)1- RSS/TSS
RSS/TSS反应的是未拟合出来的信息量的比值(比率)
1-RSS/TSS反应的就是模型能够拟合出来的信息量的比值(比率)
这就是决定系数!!!
8.4 决定系数的优点
(1)决定系数是一个相对值,数值在【0,1】之间,克服了MSE没有上边界的缺点。
(2)决定系数是一个相对值,它反应的是拟合出来的信息占样本自身总信息量的比率,这样不同样本,不同模型之间就可以进行比较了。
(3)它能够反应模型的异常效果:RSS残差平方和,不仅仅没有平均,它还通过平方的方式放大了异常拟合处的误差(残差值)值。
8.5 计算公式
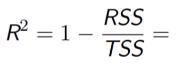
8.6 R2的几何图形
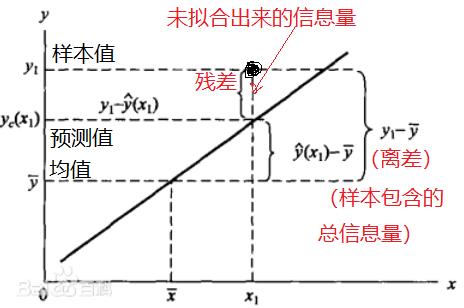
第9章 scikit-learn对测量指标的支持
9.1 所有指标展示
import sklearn
sorted(sklearn.metrics.SCORERS.keys())['accuracy', 'adjusted_mutual_info_score', 'adjusted_rand_score', 'average_precision', 'balanced_accuracy', 'completeness_score', 'explained_variance', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'fowlkes_mallows_score', 'homogeneity_score', 'jaccard', 'jaccard_macro', 'jaccard_micro', 'jaccard_samples', 'jaccard_weighted', 'max_error', 'mutual_info_score', 'neg_brier_score', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_absolute_percentage_error', 'neg_mean_gamma_deviance', 'neg_mean_poisson_deviance', 'neg_mean_squared_error', 'neg_mean_squared_log_error', 'neg_median_absolute_error', 'neg_root_mean_squared_error', 'normalized_mutual_info_score', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'rand_score', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc', 'roc_auc_ovo', 'roc_auc_ovo_weighted', 'roc_auc_ovr', 'roc_auc_ovr_weighted', 'top_k_accuracy', 'v_measure_score']
9.2 生成测试数据集
# 生成数据集 make_regression
from sklearn.datasets import make_regression
# 生成数据集
# n_samples:样本个数
# n_features:输入数据的维度,这里是1维x轴
# n_targets:输出数据的维度,这里是1为y轴
# bias:数据偏置大小
# noise:叠加的噪声大小
# random_state:随机种子
X,Y,coef = make_regression(n_samples=100, n_features=1, n_informative=1, n_targets=1, bias=5, effective_rank=None, tail_strength= 0, noise= 20, shuffle=True, coef=True, random_state=None)
print("X.shape:",X.shape)
print("Y.shape:",Y.shape)
plt.scatter(X, Y, s=20, edgecolor="black",c="darkorange", label="data")X.shape: (100, 1) Y.shape: (100,)
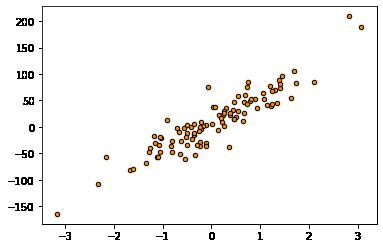
9.3 模型定义与拟合(训练)
# 模型定义与预测
from sklearn.linear_model import LinearRegression as LR
model = LR()
model = model.fit(X, Y)
# 模型预测
Y_pred = model.predict(X)
# 可视化数据
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(X, Y, s=20, edgecolor="black",c="darkorange", label="data")
plt.plot(X, Y_pred)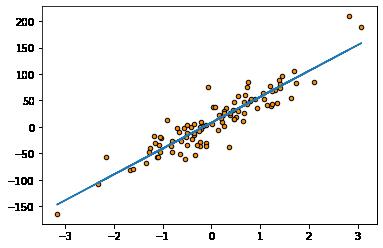
9.4 模型评估
# 模型评估
from sklearn.metrics import mean_squared_error #MSE
from sklearn.metrics import mean_absolute_error #MAE
from sklearn.metrics import r2_score #R 2
print("MAE =", mean_absolute_error(Y,Y_pred)) # 残差绝对值
print("MSE =", mean_squared_error(Y, Y_pred)) # 通过平方放大了残差
print("RMSE=", np.sqrt(mean_squared_error(Y,Y_pred))) # 通过开方,还原被放大残差
print("R^2 =", r2_score(Y,Y_pred)) # R2是相对比例值MAE = 16.585193180133935 MSE = 485.6573763120239 RMSE= 22.037635451926867 R^2 = 0.8415042235651895
9.5 交叉验证
# 通过交叉验证进行评估
from sklearn.model_selection import cross_val_score
# 对训练好的模型进行交叉验证
# cv=交叉验证的次数
# scoring:打分指标:neg_mean_squared_error,
# 在sklearn交叉验证中,损失/误差都是用负数表示,去掉负号,就是它的均分误差值
# 负号:表示损失!!!
mae_score = cross_val_score(model, X,Y,cv=5, scoring="neg_mean_absolute_error")
print("交叉验证的MAE=", mae_score.mean())
mse_score = cross_val_score(model, X,Y,cv=5, scoring="neg_mean_squared_error")
print("交叉验证的MSE=", mse_score.mean())
r2_score = cross_val_score(model, X,Y,cv=5, scoring="r2")
print("交叉验证的R2 =", r2_score.mean())交叉验证的MAE= -16.74526871947979 交叉验证的MSE= -500.88726699513006 交叉验证的R2 = 0.8103022705307797
9.6 关于scikit-learn 交叉验证时,MSE为负数的说明
在scikit-learn中,我们会发现,回归的指标MSE和MAE的指标是负数,这与我们对这两个理解是不一致的, 怎么会是负数呢?
这其实是scikit-learn实现的问题,scikit-learn认为,误差是带来负面效果的 ,因此,人为地在这些指标的计算结果之上增加了一个负号,并非这些指标的数学定义本身就是负数。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/124413449
以上是关于[机器学习与scikit-learn-51]:模型评估-图解回归模型的评估指标MSEMAERMSER2RSS与代码示例的主要内容,如果未能解决你的问题,请参考以下文章