数据挖掘机器学习[三]---汽车交易价格预测详细版本｛特征工程交叉检验绘制学习率曲线与验证曲线｝

Posted 汀、

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据挖掘机器学习[三]---汽车交易价格预测详细版本｛特征工程交叉检验绘制学习率曲线与验证曲线｝相关的知识，希望对你有一定的参考价值。

 题目出自阿里天池赛题链接：零基础入门数据挖掘 - 二手车交易价格预测-天池大赛-阿里云天池

 相关文章：

特征工程详解及实战项目【参考】

数据挖掘---汽车车交易价格预测[一](测评指标；EDA)

数据挖掘机器学习---汽车交易价格预测详细版本[二]｛EDA-数据探索性分析｝

数据挖掘机器学习---汽车交易价格预测详细版本[三]｛特征工程、交叉检验、绘制学习率曲线与验证曲线｝

数据挖掘机器学习---汽车交易价格预测详细版本[四]｛嵌入式特征选择（XGBoots,LightGBM），模型调参（贪心、网格、贝叶斯调参）｝

数据挖掘机器学习---汽车交易价格预测详细版本[五]｛模型融合(Stacking、Blending、Bagging和Boosting)｝

数据挖掘机器学习[六]---项目实战金融风控之贷款违约预测

数据挖掘机器学习[七]---2021研究生数学建模B题空气质量预报二次建模求解过程

前言

因为文档是去年弄的，很多资料都有点找不到了，我尽可能写的详细。后面以2021年研究生数学建模B题为例【空气质量预报二次建模】再进行一个教学。

首先讲几个问题：数据清洗、特征选择作用和方法。

1.常见的特征工程包括：

  1. 异常处理：
    • 通过箱线图（或 3-Sigma）分析删除异常值；
    • BOX-COX 转换（处理有偏分布）；
    • 长尾截断；
  2. 特征归一化/标准化：
    • 标准化（转换为标准正态分布）；
    • 归一化（抓换到 [0,1] 区间）；
    • 针对幂律分布，可以采用公式： log(1+x1+median)log(1+x1+median)
  3. 数据分桶：
    • 等频分桶；
    • 等距分桶；
    • Best-KS 分桶（类似利用基尼指数进行二分类）；
    • 卡方分桶；
  4. 缺失值处理：
    • 不处理（针对类似 XGBoost 等树模型）；
    • 删除（缺失数据太多）；
    • 插值补全，包括均值/中位数/众数/建模预测/多重插补/压缩感知补全/矩阵补全等；
    • 分箱，缺失值一个箱；
  5. 特征构造：
    • 构造统计量特征，报告计数、求和、比例、标准差等；
    • 时间特征，包括相对时间和绝对时间，节假日，双休日等；
    • 地理信息，包括分箱，分布编码等方法；
    • 非线性变换，包括 log/ 平方/ 根号等；
    • 特征组合，特征交叉；
    • 仁者见仁，智者见智。
  6. 特征筛选
    • 过滤式（filter）：先对数据进行特征选择，然后在训练学习器，常见的方法有 Relief/方差选择发/相关系数法/卡方检验法/互信息法；
    • 包裹式（wrapper）：直接把最终将要使用的学习器的性能作为特征子集的评价准则，常见方法有 LVM（Las Vegas Wrapper） ；
    • 嵌入式（embedding）：结合过滤式和包裹式，学习器训练过程中自动进行了特征选择，常见的有 lasso 回归；
  7. 降维
    • PCA/ LDA/ ICA；
    • 特征选择也是一种降维。

2.导入数据

（EDA部分见上一篇文章）

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from operator import itemgetter

%matplotlib inline

path = './data/'
## 1) 载入训练集和测试集；
train = pd.read_csv(path+'train.csv', sep=' ')
test = pd.read_csv(path+'testA.csv', sep=' ')
print(train.shape)
print(test.shape)

train.head()

train.columns

3.删除异常值

# 这里我包装了一个异常值处理的代码，可以随便调用。
def outliers_proc(data, col_name, scale=3):
    """
    用于清洗异常值，默认用 box_plot（scale=3）进行清洗
    :param data: 接收 pandas 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """

    def box_plot_outliers(data_ser, box_scale):
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: ".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: ".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())
    
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n
# 我们可以删掉一些异常数据，以 power 为例。  
# 这里删不删同学可以自行判断
# 但是要注意 test 的数据不能删 = = 不能掩耳盗铃是不是

train = outliers_proc(train, 'power', scale=3)
Delete number is: 963

Now column number is: 149037

Description of data less than the lower bound is:

count    0.0

mean     NaN

std      NaN

min      NaN

25%      NaN

50%      NaN

75%      NaN

max      NaN

Name: power, dtype: float64

Description of data larger than the upper bound is:

count      963.000000

mean       846.836968

std       1929.418081

min        376.000000

25%        400.000000

50%        436.000000

75%        514.000000

max      19312.000000

Name: power, dtype: float64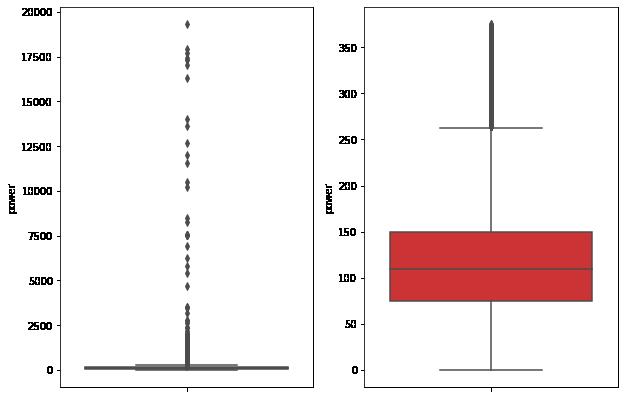

 把偏离值删除

4.特征构造

# 训练集和测试集放在一起，方便构造特征
train['train']=1
test['train']=0
data = pd.concat([train, test], ignore_index=True, sort=False)


# 使用时间：data['creatDate'] - data['regDate']，反应汽车使用时间，一般来说价格与使用时间成反比
# 不过要注意，数据里有时间出错的格式，所以我们需要 errors='coerce'
data['used_time'] = (pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') - 
                            pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days


# 看一下空数据，有 15k 个样本的时间是有问题的，我们可以选择删除，也可以选择放着。
# 但是这里不建议删除，因为删除缺失数据占总样本量过大，7.5%
# 我们可以先放着，因为如果我们 XGBoost 之类的决策树，其本身就能处理缺失值，所以可以不用管；
data['used_time'].isnull().sum()


# 从邮编中提取城市信息，因为是德国的数据，所以参考德国的邮编，相当于加入了先验知识
data['city'] = data['regionCode'].apply(lambda x : str(x)[:-3])


# 计算某品牌的销售统计量，同学们还可以计算其他特征的统计量
# 这里要以 train 的数据计算统计量
train_gb = train.groupby("brand")
all_info = 
for kind, kind_data in train_gb:
    info = 
    kind_data = kind_data[kind_data['price'] > 0]
    info['brand_amount'] = len(kind_data)
    info['brand_price_max'] = kind_data.price.max()
    info['brand_price_median'] = kind_data.price.median()
    info['brand_price_min'] = kind_data.price.min()
    info['brand_price_sum'] = kind_data.price.sum()
    info['brand_price_std'] = kind_data.price.std()
    info['brand_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)
    all_info[kind] = info
brand_fe = pd.DataFrame(all_info).T.reset_index().rename(columns="index": "brand")
data = data.merge(brand_fe, how='left', on='brand')


# 数据分桶 以 power 为例
# 这时候我们的缺失值也进桶了，
# 为什么要做数据分桶呢，原因有很多，= =
# 1. 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
# 2. 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
# 3. LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
# 4. 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
# 5. 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化

# 当然还有很多原因，LightGBM 在改进 XGBoost 时就增加了数据分桶，增强了模型的泛化性

bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
data[['power_bin', 'power']].head()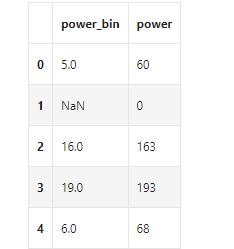

# 利用好了，就可以删掉原始数据了
data = data.drop(['creatDate', 'regDate', 'regionCode'], axis=1)

print(data.shape)
data.columns

# 目前的数据其实已经可以给树模型使用了，所以我们导出一下
data.to_csv('data_for_tree.csv', index=0)

# 我们可以再构造一份特征给 LR NN 之类的模型用
# 之所以分开构造是因为，不同模型对数据集的要求不同
# 我们看下数据分布：
data['power'].plot.hist()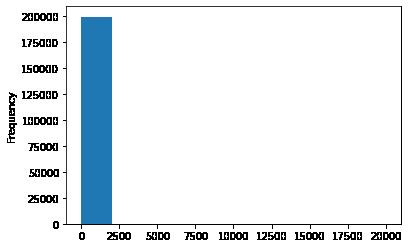

# 我们刚刚已经对 train 进行异常值处理了，但是现在还有这么奇怪的分布是因为 test 中的 power 异常值，
# 所以我们其实刚刚 train 中的 power 异常值不删为好，可以用长尾分布截断来代替
train['power'].plot.hist()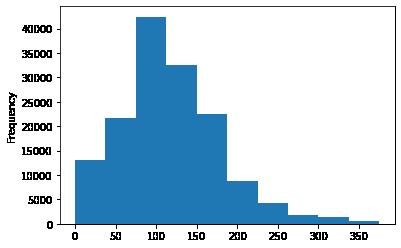

# 我们对其取 log，在做归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
data['power'] = np.log(data['power'] + 1) 
data['power'] = ((data['power'] - np.min(data['power'])) / (np.max(data['power']) - np.min(data['power'])))
data['power'].plot.hist()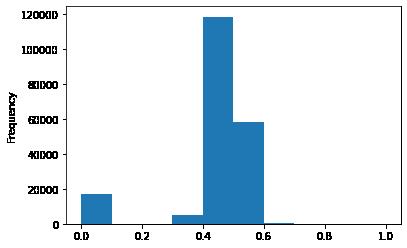

# km 的比较正常，应该是已经做过分桶了
data['kilometer'].plot.hist()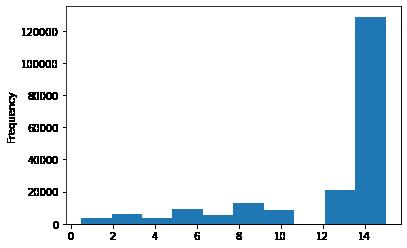

# 所以我们可以直接做归一化
data['kilometer'] = ((data['kilometer'] - np.min(data['kilometer'])) / 
                        (np.max(data['kilometer']) - np.min(data['kilometer'])))
data['kilometer'].plot.hist()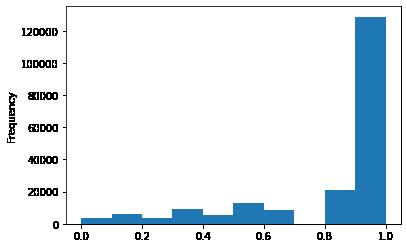

# 除此之外 还有我们刚刚构造的统计量特征：
# 'brand_amount', 'brand_price_average', 'brand_price_max',
# 'brand_price_median', 'brand_price_min', 'brand_price_std',
# 'brand_price_sum'
# 这里不再一一举例分析了，直接做变换，
def max_min(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))

data['brand_amount'] = ((data['brand_amount'] - np.min(data['brand_amount'])) / 
                        (np.max(data['brand_amount']) - np.min(data['brand_amount'])))
data['brand_price_average'] = ((data['brand_price_average'] - np.min(data['brand_price_average'])) / 
                               (np.max(data['brand_price_average']) - np.min(data['brand_price_average'])))
data['brand_price_max'] = ((data['brand_price_max'] - np.min(data['brand_price_max'])) / 
                           (np.max(data['brand_price_max']) - np.min(data['brand_price_max'])))
data['brand_price_median'] = ((data['brand_price_median'] - np.min(data['brand_price_median'])) /
                              (np.max(data['brand_price_median']) - np.min(data['brand_price_median'])))
data['brand_price_min'] = ((data['brand_price_min'] - np.min(data['brand_price_min'])) / 
                           (np.max(data['brand_price_min']) - np.min(data['brand_price_min'])))
data['brand_price_std'] = ((data['brand_price_std'] - np.min(data['brand_price_std'])) / 
                           (np.max(data['brand_price_std']) - np.min(data['brand_price_std'])))
data['brand_price_sum'] = ((data['brand_price_sum'] - np.min(data['brand_price_sum'])) / 
                           (np.max(data['brand_price_sum']) - np.min(data['brand_price_sum'])))

 one-hote编码

# 对类别特征进行 OneEncoder
data = pd.get_dummies(data, columns=['model', 'brand', 'bodyType', 'fuelType',
                                     'gearbox', 'notRepairedDamage', 'power_bin'])
print(data.shape)
data.columns

(199037, 370)
Index(['SaleID', 'name', 'power', 'kilometer', 'seller', 'offerType', 'price',
,       'v_0', 'v_1', 'v_2',
,       ...
,       'power_bin_20.0', 'power_bin_21.0', 'power_bin_22.0', 'power_bin_23.0',
,       'power_bin_24.0', 'power_bin_25.0', 'power_bin_26.0', 'power_bin_27.0',
,       'power_bin_28.0', 'power_bin_29.0'],
,      dtype='object', length=370)
# 这份数据可以给 LR 用
data.to_csv('data_for_lr.csv', index=0)

5.特征筛选

5.1 过滤式

其中：只有符合正态分布，才能使用皮尔森相关性分析

# 相关性分析
print(data['power'].corr(data['price'], method='spearman'))
print(data['kilometer'].corr(data['price'], method='spearman'))
print(data['brand_amount'].corr(data['price'], method='spearman'))
print(data['brand_price_average'].corr(data['price'], method='spearman'))
print(data['brand_price_max'].corr(data['price'], method='spearman'))
print(data['brand_price_median'].corr(data['price'], method='spearman'))


0.5728285196051496

-0.4082569701616764

0.058156610025581514

0.3834909576057687

0.259066833880992

0.38691042393409447

可以看到0.05：相关性比较小，可以考虑删除，对比删不删之后的效果

# 当然也可以直接看图
data_numeric = data[['power', 'kilometer', 'brand_amount', 'brand_price_average', 
                     'brand_price_max', 'brand_price_median']]
correlation = data_numeric.corr()

f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,  vmax=0.8)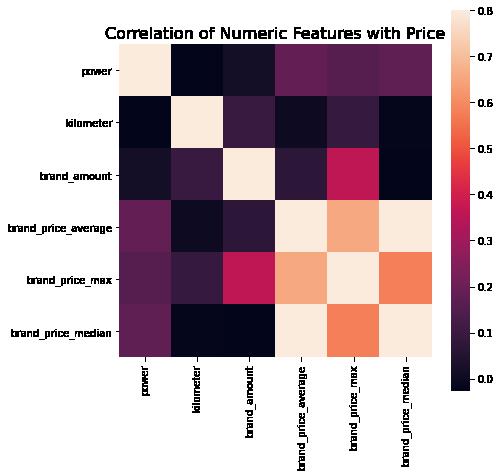

 5.2 包裹式

!pip install mlxtend


# k_feature 太大会很难跑，没服务器，所以提前 interrupt 了
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LinearRegression
sfs = SFS(LinearRegression(),
           k_features=10,
           forward=True,
           floating=False,
           scoring = 'r2',
           cv = 0)
x = data.drop(['price'], axis=1)
numerical_cols = x.select_dtypes(exclude = 'object').columns
x = x[numerical_cols]
x = x.fillna(0)
y = data['price'].fillna(0)
sfs.fit(x, y)
sfs.k_feature_names_

mlxtend是一个机器学习的库很强大，集成学习主要分为 bagging， boosting 和 stacking方法

其余常见库包括（pandas、numpy、sklearn、mlxtend）。

选出来的特征如下：【主要修改参数在sfs中修改】

('kilometer',
, 'v_0',
, 'v_3',
, 'v_7',
, 'train',
, 'used_time',
, 'brand_price_average',
, 'brand_price_std',
, 'model_167.0',
, 'gearbox_1.0')
# 画出来，可以看到边际效益
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
import matplotlib.pyplot as plt
fig1 = plot_sfs(sfs.get_metric_dict(), kind='std_dev')
plt.grid()
plt.show()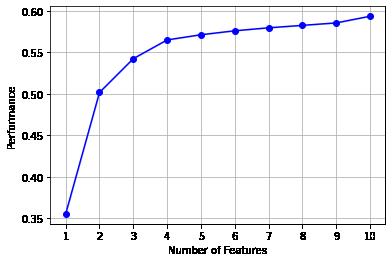

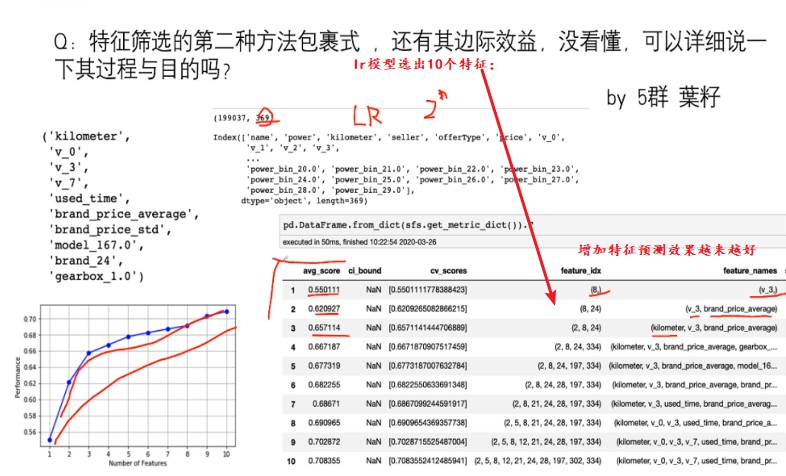
5.3嵌入式

将会在下一篇博客详细讲解

6. 通过线性回归进行仿真分析

6.1 读取数据，调整数据类型减少内存占用

import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')

reduce_mem_usage 函数通过调整数据类型，帮助我们减少数据在内存中占用的空间

def reduce_mem_usage(df):
    """ iterate through all the columns of a dataframe and modify the data type
        to reduce memory usage.        
    """
    start_mem = df.memory_usage().sum() 
    print('Memory usage of dataframe is :.2f MB'.format(start_mem))
    
    for col in df.columns:
        col_type = df[col].dtype
        
        if col_type != object:
            c_min = df[col].min()
            c_max = df[col].max()
            if str(col_type)[:3] == 'int':
                if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
                    df[col] = df[col].astype(np.int8)
                elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
                    df[col] = df[col].astype(np.int16)
                elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
                    df[col] = df[col].astype(np.int32)
                elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
                    df[col] = df[col].astype(np.int64)  
            else:
                if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
                    df[col] = df[col].astype(np.float16)
                elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
                    df[col] = df[col].astype(np.float32)
                else:
                    df[col] = df[col].astype(np.float64)
        else:
            df[col] = df[col].astype('category')

    end_mem = df.memory_usage().sum() 
    print('Memory usage after optimization is: :.2f MB'.format(end_mem))
    print('Decreased by :.1f%'.format(100 * (start_mem - end_mem) / start_mem))
    return df
sample_feature = reduce_mem_usage(pd.read_csv('data_for_tree.csv'))
Memory usage of dataframe is 62099672.00 MB

Memory usage after optimization is: 16520303.00 MB

Decreased by 73.4%
continuous_feature_names = [x for x in sample_feature.columns if x not in ['price','brand','model','brand']]

6.2 线性回归 & 五折交叉验证 & 模拟真实业务情况

sample_feature = sample_feature.dropna().replace('-', 0).reset_index(drop=True)
sample_feature['notRepairedDamage'] = sample_feature['notRepairedDamage'].astype(np.float32)
train = sample_feature[continuous_feature_names + ['price']]

train_X = train[continuous_feature_names]
train_y = train['price']

6.2.1 简单建模：

from sklearn.linear_model import LinearRegression

model = LinearRegression(normalize=True)

model = model.fit(train_X, train_y)

'intercept:'+ str(model.intercept_)

查看训练的线性回归模型的截距（intercept）与权重(coef)

sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)

from matplotlib import pyplot as plt

subsample_index = np.random.randint(low=0, high=len(train_y), size=50)

绘制特征v_9的值与标签的散点图，图片发现模型的预测结果（蓝色点）与真实标签（黑色点）的分布差异较大，且部分预测值出现了小于0的情况，说明我们的模型存在一些问题

plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_X['v_9'][subsample_index], model.predict(train_X.loc[subsample_index]), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price is obvious different from true price')
plt.show()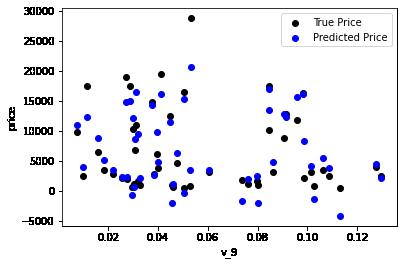

 通过作图我们发现数据的标签（price）呈现长尾分布，不利于我们的建模预测。原因是很多模型都假设数据误差项符合正态分布，而长尾分布的数据违背了这一假设

import seaborn as sns
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y)
plt.subplot(1,2,2)
sns.distplot(train_y[train_y < np.quantile(train_y, 0.9)])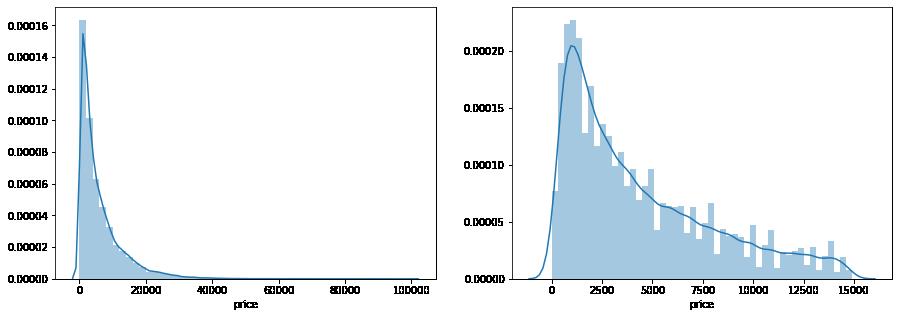

 在这里我们对标签进行了 log(x+1)log(x+1) 变换，使标签贴近于正态分布

train_y_ln = np.log(train_y + 1)

import seaborn as sns
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y_ln)
plt.subplot(1,2,2)
sns.distplot(train_y_ln[train_y_ln < np.quantile(train_y_ln, 0.9)])


model = model.fit(train_X, train_y_ln)

print('intercept:'+ str(model.intercept_))
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)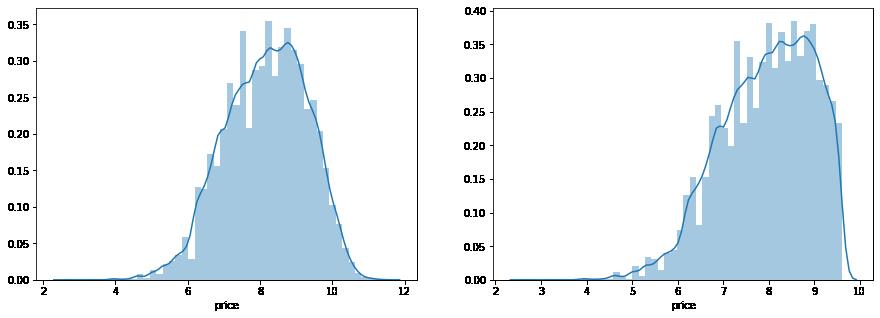

再次进行可视化，发现预测结果与真实值较为接近，且未出现异常状况

plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_X['v_9'][subsample_index], np.exp(model.predict(train_X.loc[subsample_index])), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price seems normal after np.log transforming')
plt.show()

6.2.2 五折交叉验证

 在使用训练集对参数进行训练的时候，经常会发现人们通常会将一整个训练集分为三个部分（比如mnist手写训练集）。一般分为：训练集（train_set），评估集（valid_set），测试集（test_set）这三个部分。这其实是为了保证训练效果而特意设置的。其中测试集很好理解，其实就是完全不参与训练的数据，仅仅用来观测测试效果的数据。而训练集和评估集则牵涉到下面的知识了。

因为在实际的训练中，训练的结果对于训练集的拟合程度通常还是挺好的（初始条件敏感），但是对于训练集之外的数据的拟合程度通常就不那么令人满意了。因此我们通常并不会把所有的数据集都拿来训练，而是分出一部分来（这一部分不参加训练）对训练集生成的参数进行测试，相对客观的判断这些参数对训练集之外的数据的符合程度。这种思想就称为交叉验证（Cross Validation）

from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error,  make_scorer

def log_transfer(func):
    def wrapper(y, yhat):
        result = func(np.log(y), np.nan_to_num(np.log(yhat)))
        return result
    return wrapper

scores = cross_val_score(model, X=train_X, y=train_y, verbose=1, cv = 5, scoring=make_scorer(log_transfer(mean_absolute_error)))

使用线性回归模型，对未处理标签的特征数据进行五折交叉验证
print('AVG:', np.mean(scores))
使用线性回归模型，对处理过标签的特征数据进行五折交叉验证
scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=1, cv = 5, scoring=make_scorer(mean_absolute_error))

print('AVG:', np.mean(scores))
AVG: 0.1932530155796405

scores = pd.DataFrame(scores.reshape(1,-1))
scores.columns = ['cv' + str(x) for x in range(1, 6)]
scores.index = ['MAE']
scores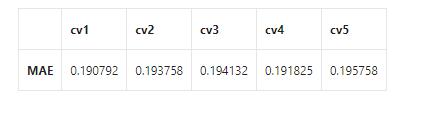

 6.2.3 模拟真实业务情况

但在事实上，由于我们并不具有预知未来的能力，五折交叉验证在某些与时间相关的数据集上反而反映了不真实的情况。通过2018年的二手车价格预测2017年的二手车价格，这显然是不合理的，因此我们还可以采用时间顺序对数据集进行分隔。在本例中，我们选用靠前时间的4/5样本当作训练集，靠后时间的1/5当作验证集，最终结果与五折交叉验证差距不大

import datetime
sample_feature = sample_feature.reset_index(drop=True)
split_point = len(sample_feature) // 5 * 4
train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()

train_X = train[continuous_feature_names]
train_y_ln = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_y_ln = np.log(val['price'] + 1)
model = model.fit(train_X, train_y_ln)
mean_absolute_error(val_y_ln, model.predict(val_X))

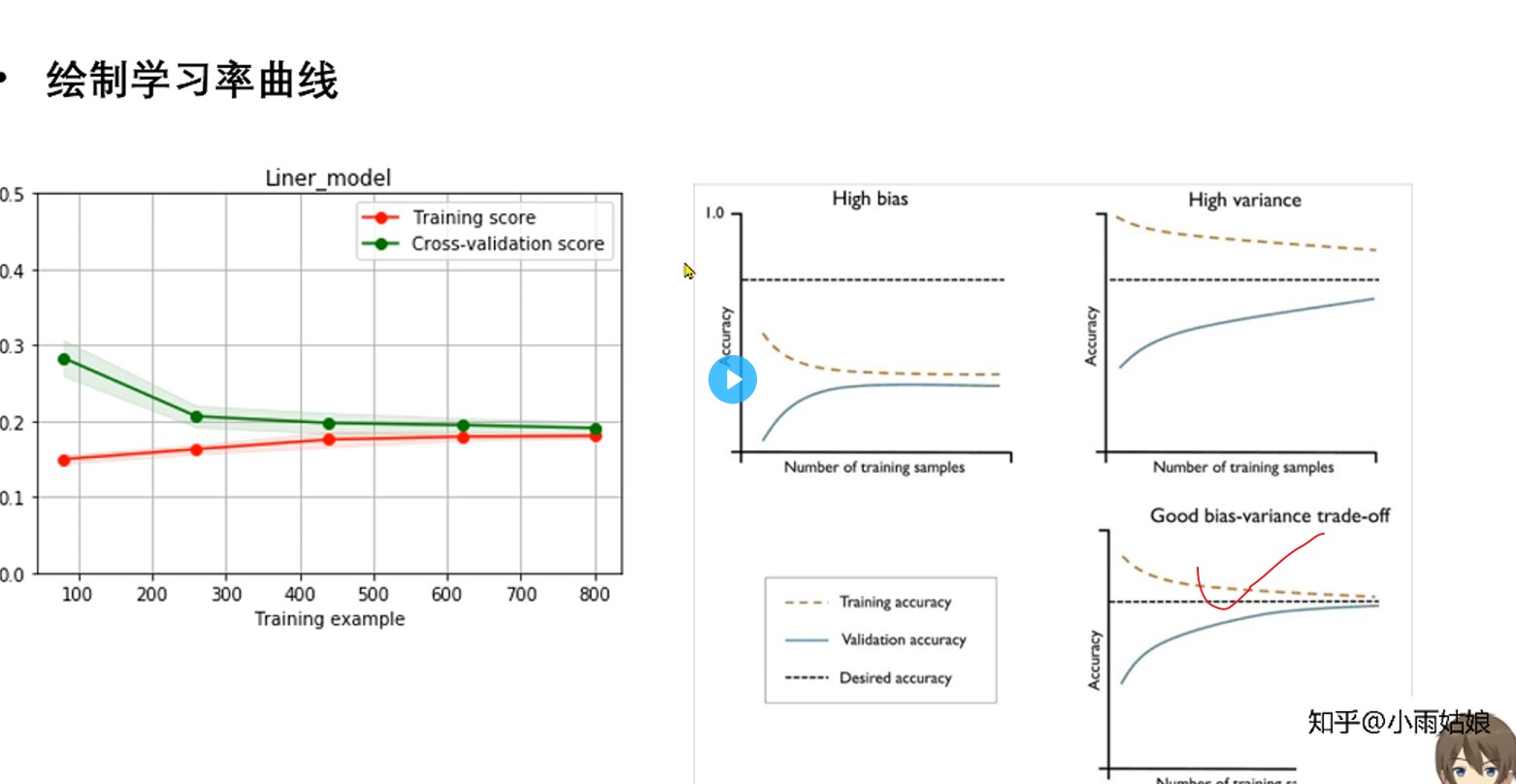
0.19577667149549233

6.2.4 绘制学习率曲线与验证曲线

from sklearn.model_selection import learning_curve, validation_curve

? learning_curve 查看功能
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,n_jobs=1, train_size=np.linspace(.1, 1.0, 5 )):  
    plt.figure()  
    plt.title(title)  
    if ylim is not None:  
        plt.ylim(*ylim)  
    plt.xlabel('Training example')  
    plt.ylabel('score')  
    train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_size, scoring = make_scorer(mean_absolute_error))  
    train_scores_mean = np.mean(train_scores, axis=1)  
    train_scores_std = np.std(train_scores, axis=1)  
    test_scores_mean = np.mean(test_scores, axis=1)  
    test_scores_std = np.std(test_scores, axis=1)  
    plt.grid()#区域  
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,  
                     train_scores_mean + train_scores_std, alpha=0.1,  
                     color="r")  
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,  
                     test_scores_mean + test_scores_std, alpha=0.1,  
                     color="g")  
    plt.plot(train_sizes, train_scores_mean, 'o-', color='r',  
             label="Training score")  
    plt.plot(train_sizes, test_scores_mean,'o-',color="g",  
             label="Cross-validation score")  
    plt.legend(loc="best")  
    return plt  
plot_learning_curve(LinearRegression(), 'Liner_model', train_X[:1000], train_y_ln[:1000], ylim=(0.0, 0.5), cv=5, n_jobs=1)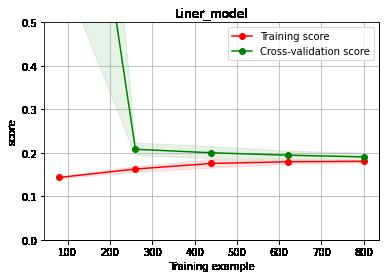

 嵌入式特征选择将会在下一个博客进行讲解

阅读世界，共赴山海 423全民读书节，邀你共读

以上是关于数据挖掘机器学习[三]---汽车交易价格预测详细版本｛特征工程交叉检验绘制学习率曲线与验证曲线｝的主要内容，如果未能解决你的问题，请参考以下文章

数据挖掘机器学习[五]---汽车交易价格预测详细版本｛模型融合(StackingBlendingBagging和Boosting)｝

｝

数据挖掘机器学习[四]---汽车交易价格预测详细版本｛嵌入式特征选择（XGBoots,LightGBM），模型调参（贪心网格贝叶斯调参）｝

｝

数据挖掘机器学习[六]---项目实战金融风控之贷款违约预测

ML之R：通过数据预处理利用LiR/XGBoost等(特征重要性/交叉训练曲线可视化/线性和非线性算法对比/三种模型调参/三种模型融合)实现二手汽车产品交易价格回归预测之详细攻略