ACM入门之容斥定理

Posted 2022-04-22 辉小歌

看上图可能会很迷，我们直接看例题。
例题一:

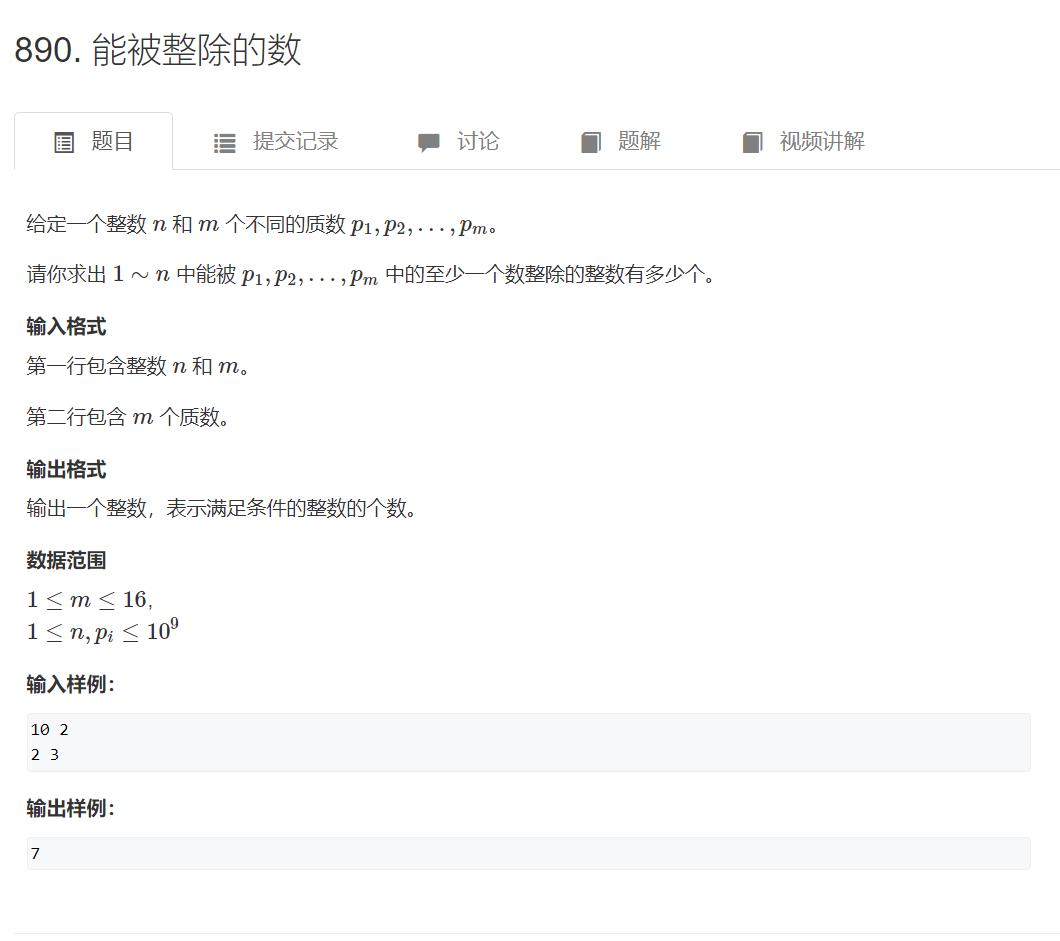
很经典的容斥，我们可以用二进制枚举来枚举所有的集合。
对于每一个集合的正负号，就是该集合内的集合数。例如:

#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL a[25],n,m,sum;
LL solve(LL n)

    LL sum=0;
    for(int i=1;i<(1<<m);i++)//注意从1开始
    
        LL temp=n,cnt=-1;
        for(int j=0;j<m;j++)
        
            if(i>>j&1)
            
                temp/=a[j],cnt=cnt*(-1);
            
        
        sum=sum+cnt*temp;
    
    return sum;

int main(void)

    cin>>n>>m;
    for(int i=0;i<m;i++) cin>>a[i];
    cout<<solve(n);
    return 0;

例题二：

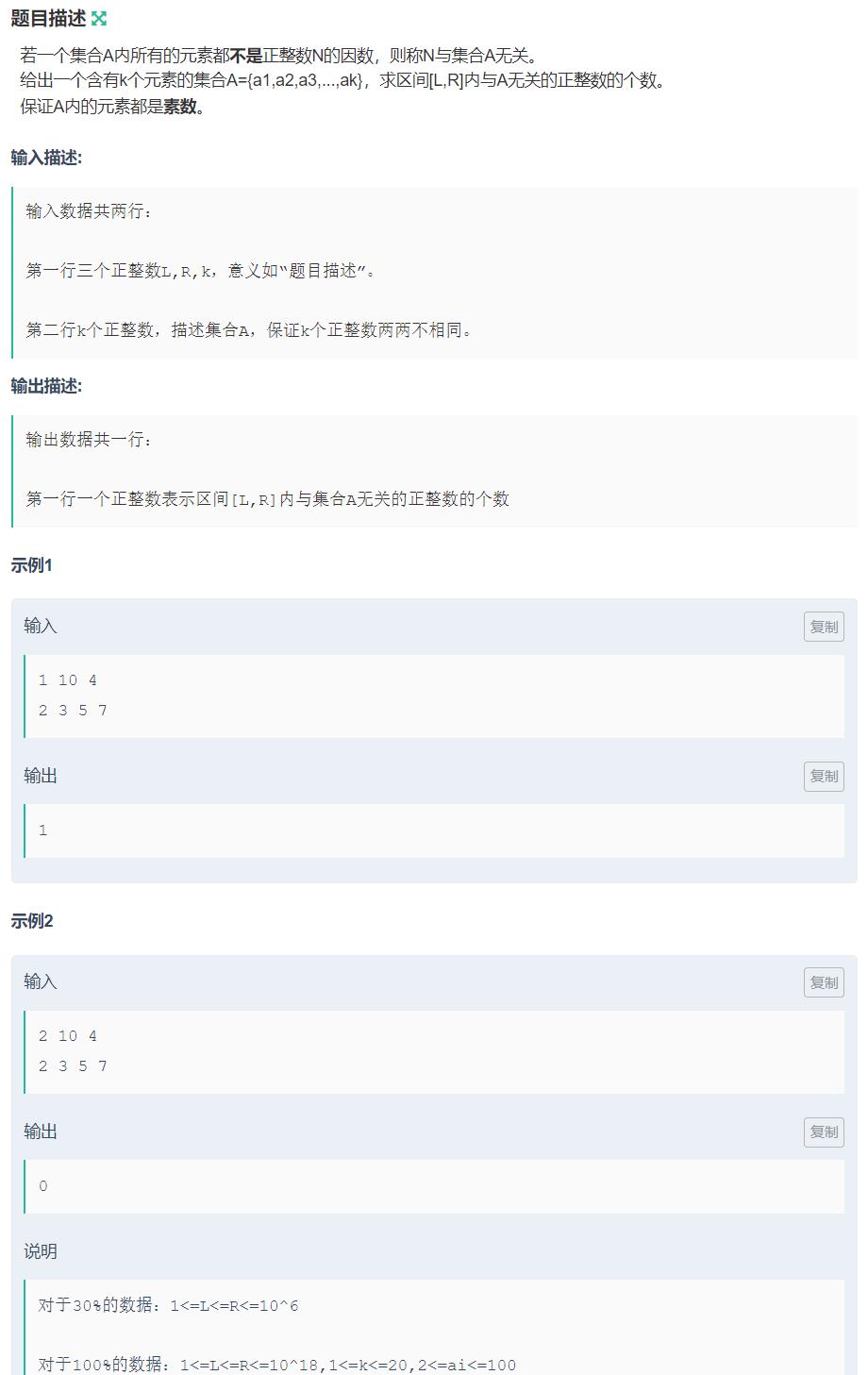
#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=25;
LL l,r,n,a[N];
LL solve(LL x)

	LL sum=0;
	for(int i=1;i<(1<<n);i++)
	
		LL temp=x,cnt=-1;
		for(int j=0;j<n;j++)
		
			if((i>>j)&1==1) temp/=a[j],cnt=cnt*(-1);
		
		sum=sum+cnt*temp;
	
	return x-sum;

int main(void)

	cin>>l>>r>>n;
	for(int i=0;i<n;i++) cin>>a[i];
	cout<<solve(r)-solve(l-1);
	return 0;