适于Large Prime Characteristic Fields的高效算法及其在Bilinear Pairing和Supersingular Isogeny-Based协议中的应用

Posted 2022-04-22 mutourend

1. 引言

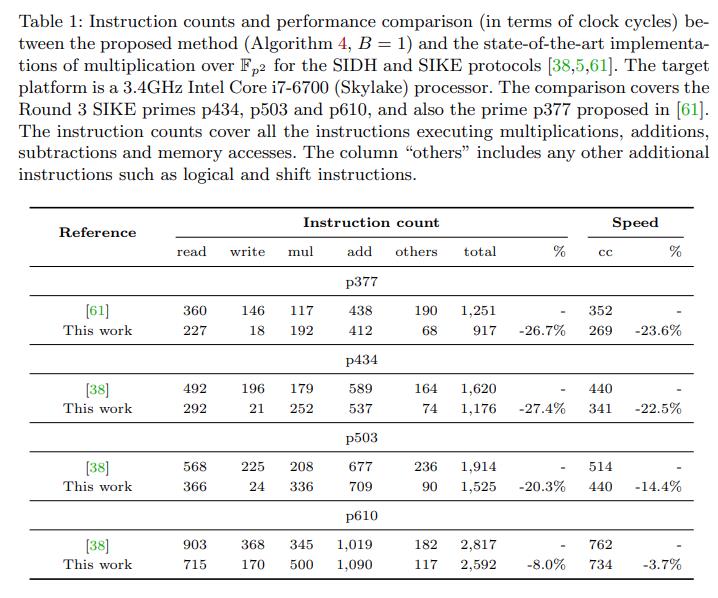
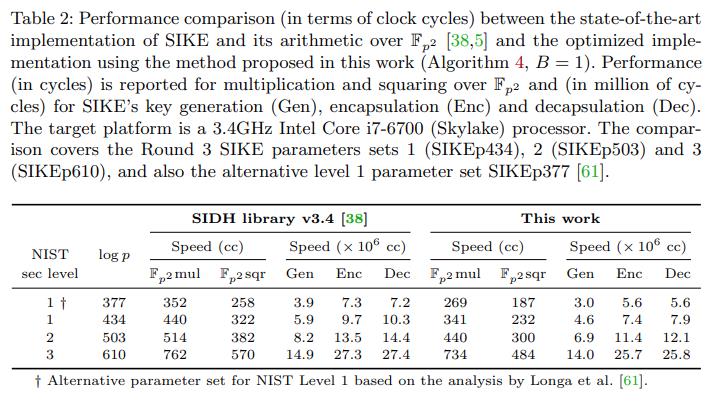
微软团队Patrick Longa 2022年论文 《Efficient Algorithms for Large Prime Characteristic Fields and Their Application to Bilinear Pairings and Supersingular Isogeny-Based Protocols》，在该论文中提出了一种通用 interleaved modular multiplication算法，可用于基于large prime field的sum of product计算。该算法重新制定了目前广泛使用的lazy reduction技术，重点规避了the need for storage and computation of “double-precision” operations。此外，它可以很容易地适应现有的计算modular multiplication的不同方法，从而产生效率更高、内存更友好的算法。在该论文中，对computation of multiplication over an extension field ${\mathbb{F}}_{q^k}$进行了性能比对：

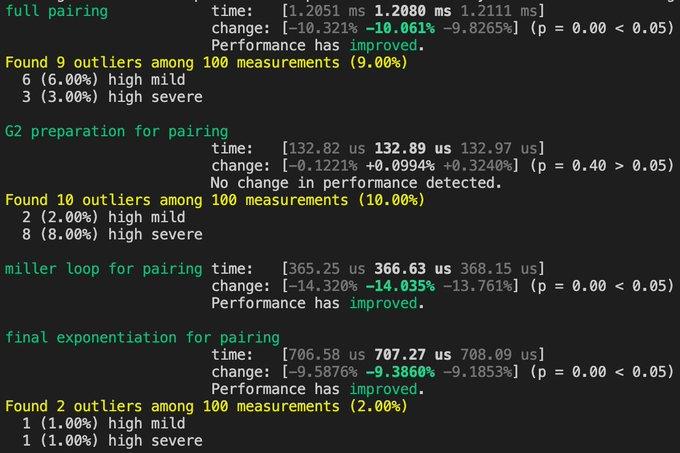
• 1）对于bilinear pairings：在x64 Intel处理器上，基于流行的BLS12-2381曲线的optimal ate pairing计算，速度提升了1.37x。
• 2）对于supersingular isogeny-based protocols：在x64 Intel处理器上，基于SIKE protocol的计算，速度提升了1.30x。

相关代码实现见：

• https://github.com/microsoft/PQCrypto-SIDH（C语言）
• https://github.com/zkcrypto/bls12_381/tree/efficient-extension-field-arithmetic（Rust语言）【针对multiplication over ${\mathbb{F}}_p$、${\mathbb{F}}_{p^2}$、${\mathbb{F}}_{p^6}$】
  

$(a_0,a_1,\cdots ,a_{t-1}),(b_0,b_1,\cdots ,b_{t-2})$这2个集合内所有元素均属于特定域${\mathbb{F}}_p$ of large prime characteristic $p$，所谓sum of products是指类似如下的计算：
$c={\sum }_{i=0}^{t-1}\pm a_i\cdot b_i\mathrm{m}\mathrm{o}\mathrm{d}p$

该操作是很多密码学计算的核心，最有名的可能就是multiplication over extension fields with large prime characteristic。

同时，若$a,b\in {\mathbb{F}}_{q^k}$，需计算$a\cdot b\mathrm{m}\mathrm{o}\mathrm{d}f$，其中$f=x^k-w$，其中$w$为a primitive element in ${\mathbb{F}}_p^{\ast }$且$k|(p-1)$。则相应的多项式乘积为：

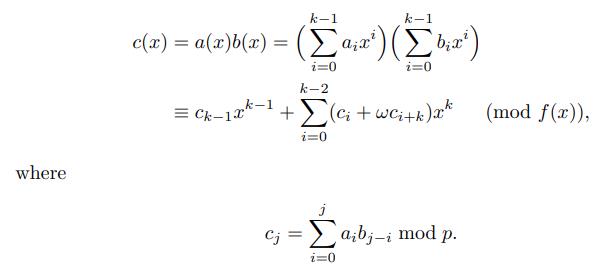
一种广泛的优化实践是使用“accumulation and reduction”策略来优化计算每个$c_j$，该策略也称为lazy reduction——可将modular reduction的数量建委1次（或k次，对于整个多项式乘积来说）。在很多使用场景中，假设$w$具有small coefficients，使得乘积相对便宜。
但是，lazy reduction的主要缺陷在于，需要额外的存储并计算double precision的中间结果。

https://github.com/zkcrypto/bls12_381/tree/efficient-extension-field-arithmetic中针对BL12_381的multiplication over ${\mathbb{F}}_p$为：

	/// Returns `c = a.zip(b).fold(0, |acc, (a_i, b_i)| acc + a_i * b_i)`.
    ///
    /// Implements Algorithm 2 from Patrick Longa's
    /// [ePrint 2022-367](https://eprint.iacr.org/2022/367) §3.
    #[inline]
    pub(crate) fn sum_of_products<const T: usize>(a: [Fp; T], b: [Fp; T]) -> Fp 
        // For a single `a x b` multiplication, operand scanning (schoolbook) takes each
        // limb of `a` in turn, and multiplies it by all of the limbs of `b` to compute
        // the result as a double-width intermediate representation, which is then fully
        // reduced at the end. Here however we have pairs of multiplications (a_i, b_i),
        // the results of which are summed.
        //
        // The intuition for this algorithm is two-fold:
        // - We can interleave the operand scanning for each pair, by processing the jth
        //   limb of each `a_i` together. As these have the same offset within the overall
        //   operand scanning flow, their results can be summed directly.
        // - We can interleave the multiplication and reduction steps, resulting in a
        //   single bitshift by the limb size after each iteration. This means we only
        //   need to store a single extra limb overall, instead of keeping around all the
        //   intermediate results and eventually having twice as many limbs.

        // Algorithm 2, line 2
        let (u0, u1, u2, u3, u4, u5) =
            (0..6).fold((0, 0, 0, 0, 0, 0), |(u0, u1, u2, u3, u4, u5), j| 
                // Algorithm 2, line 3
                // For each pair in the overall sum of products:
                let (t0, t1, t2, t3, t4, t5, t6) = (0..T).fold(
                    (u0, u1, u2, u3, u4, u5, 0),
                    |(t0, t1, t2, t3, t4, t5, t6), i| 
                        // Compute digit_j x row and accumulate into `u`.
                        let (t0, carry) = mac(t0, a[i].0[j], b[i].0[0], 0);
                        let (t1, carry) = mac(t1, a[i].0[j], b[i].0[1], carry);
                        let (t2, carry) = mac(t2, a[i].0[j], b[i].0[2], carry);
                        let (t3, carry) = mac(t3, a[i].0[j], b[i].0[3], carry);
                        let (t4, carry) = mac(t4, a[i].0[j], b[i].0[4], carry);
                        let (t5, carry) = mac(t5, a[i].0[j], b[i].0[5], carry);
                        let (t6, _) = adc(t6, 0, carry);

                        (t0, t1, t2, t3, t4, t5, t6)
                    ,
                );

                // Algorithm 2, lines 4-5
                // This is a single step of the usual Montgomery reduction process.
                let k = t0.wrapping_mul(INV);
                let (_, carry) = mac(t0, k, MODULUS[0], 0);
                let (r1, carry) = mac(t1, k, MODULUS[1], carry);
                let (r2, carry) = mac(t2, k, MODULUS[2], carry);
                let (r3, carry) = mac(t3, k, MODULUS[3], carry);
                let (r4, carry) = mac(t4, k, MODULUS[4], carry);
                let (r5, carry) = mac(t5, k, MODULUS[5], carry);
                let (r6, _) = adc(t6, 0, carry);

                (r1, r2, r3, r4, r5, r6)
            );

        // Because we represent F_p elements in non-redundant form, we need a final
        // conditional subtraction to ensure the output is in range.
        (&Fp([u0, u1, u2, u3, u4, u5])).subtract_p()
    

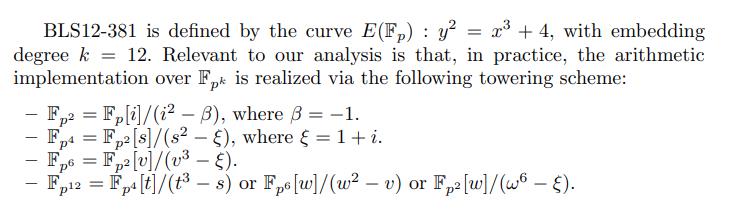
https://github.com/zkcrypto/bls12_381/tree/efficient-extension-field-arithmetic中针对BL12_381的multiplication over ${\mathbb{F}}_{p^2}$为：

	pub fn mul(&self, rhs: &Fp2) -> Fp2 
        // F_p^2 x F_p^2 multiplication implemented with operand scanning (schoolbook)
        // computes the result as:
        //
        //   a·b = (a_0 b_0 + a_1 b_1 β) + (a_0 b_1 + a_1 b_0)i
        //
        // In BLS12-381's F_p^2, our β is -1, so the resulting F_p^2 element is:
        //
        //   c_0 = a_0 b_0 - a_1 b_1
        //   c_1 = a_0 b_1 + a_1 b_0
        //
        // Each of these is a "sum of products", which we can compute efficiently.

        Fp2 
            c0: Fp::sum_of_products([self.c0, -self.c1], [rhs.c0, rhs.c1]),
            c1: Fp::sum_of_products([self.c0, self.c1], [rhs.c1, rhs.c0]),
        
    

https://github.com/zkcrypto/bls12_381/tree/efficient-extension-field-arithmetic中针对BL12_381的multiplication over ${\mathbb{F}}_{p^6}$为：

impl<'a, 'b> Mul<&'b Fp6> for &'a Fp6 
    type Output = Fp6;

    #[inline]
    fn mul(self, other: &'b Fp6) -> Self::Output 
        self.mul_interleaved(other)
    

	/// Returns `c = self * b`.
    ///
    /// Implements the full-tower interleaving strategy from
    /// [ePrint 2022-376](https://eprint.iacr.org/2022/367).
    #[inline]
    fn mul_interleaved(&self, b: &Self) -> Self 
        // The intuition for this algorithm is that we can look at F_p^6 as a direct
        // extension of F_p^2, and express the overall operations down to the base field
        // F_p instead of only over F_p^2. This enables us to interleave multiplications
        // and reductions, ensuring that we don't require double-width intermediate
        // representations (with around twice as many limbs as F_p elements).

        // We want to express the multiplication c = a x b, where a = (a_0, a_1, a_2) is
        // an element of F_p^6, and a_i = (a_i,0, a_i,1) is an element of F_p^2. The fully
        // expanded multiplication is given by (2022-376 §5):
        //
        //   c_0,0 = a_0,0 b_0,0 - a_0,1 b_0,1 + a_1,0 b_2,0 - a_1,1 b_2,1 + a_2,0 b_1,0 - a_2,1 b_1,1
        //                                     - a_1,0 b_2,1 - a_1,1 b_2,0 - a_2,0 b_1,1 - a_2,1 b_1,0.
        //         = a_0,0 b_0,0 - a_0,1 b_0,1 + a_1,0 (b_2,0 - b_2,1) - a_1,1 (b_2,0 + b_2,1)
        //                                     + a_2,0 (b_1,0 - b_1,1) - a_2,1 (b_1,0 + b_1,1).
        //
        //   c_0,1 = a_0,0 b_0,1 + a_0,1 b_0,0 + a_1,0 b_2,1 + a_
以上是关于适于Large Prime Characteristic Fields的高效算法及其在Bilinear Pairing和Supersingular Isogeny-Based协议中的应用的主要内容，如果未能解决你的问题，请参考以下文章
 
 Mecanim动画系统
 线性筛
 方法调用可能会产生“NullPointerException”
 解决pip下载速度过慢及超时等其它的报错的方法适于多种操作系统（详细）
 Spoj PRIME1 - Prime Generator
 kibana页面报错Data too large