机器学习笔记

Posted 2022-04-22 鼠尾草的第24个朋友

机器学习笔记（一）

什么是机器学习

机器学习概括来说可以用一句话来描述机器学习这件事，机器学习就是让机器具备找一个函式的能力。具体的说，机器学习就是找到一个复杂的函数，将我们输入的东西输出期待的值。可以是输入图片，输出图片中的信息，也可以是语音输入，输出文字。机器学习就是寻找建立在输入和输出之间的函数。

机器学习的三大任务

Regression

Regression的意思是说，假设我们今天要找的函式，他的输出是一个数值，他的输出是一个scalar，那这样子的机器学习的任务，我们称之为Regression。

Classification

Classification这个任务，要机器做的是选择题，我们人类，先准备好一些选项，这些选项，又叫作类别（classes），我们现在要找的函式它的输出，就是从我们设定好的选项里面，选择一个当作输出，这个任务就叫作Classification。

Structured Learning

机器今天不只是要做选择题，不只是输出一个数字 还要产生一个有结构的物件，举例来说，机器画一张图、写一篇文章，这种叫机器产生有结构的东西的问题，就叫作Structured Learning。

机器学习的步骤

1. Function with Unknown Parameters

对于实际问题而言，第一个步骤往往是写出一个带有未知参数的函数，简单的说就是，我们先猜测一下我们要找的这个函数$F$，他的数学式子到底长什么样，先做一个最简单的猜测：$$y=b+\omega x$$

• y是我们准备要预测的东西
• x是我们已知的东西
• $\omega$和$b$是位置的参数，也是机器要学习的内容，$\omega$叫它weight，$b$叫它Bias

这个带有 Unknown 的 Paramete r的 Function，我们就叫做 Model。

2. Define Loss from Training Data

第二个步骤是要定义一个名字叫做Loss的Function，这个Function的输入是我们Model的参数，输出的值代表着这个Model的拟合程度。通俗的讲就是根据我们已知模型输出的值和实际的值（Label）进行对比，通过一种计算方式的出已知模型和真是数据的差距。方法有很多种，计算y跟ŷ绝对值再相加得到Loss的方法叫做mean absolute error，缩写是MAE，计算y跟ŷ相减y平方算出来的，这个叫mean square error，缩写是MSE，还有Cross-entropy等算法。

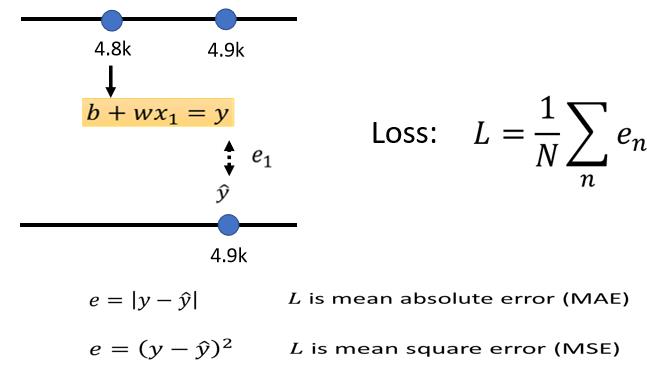
Loss越大，代表我们现在这一组参数越不好，这个大L越小，代表现在这一组参数越好。根据Loss对不同$\omega$和$b$的变化我们可以做出Error Surface（误差曲面），可视化如图：

在这个等高线图上面，越偏红色系，代表计算出来的Loss越大，就代表这一组w跟b越差，如果越偏蓝色系，就代表Loss越小，就代表这一组w跟b越好。

3. Optimization

第三步要做的事情，其实是解一个最佳化的问题，就是找一个特定的$\omega$和$b$代进去，可以让我们的Loss最小，这个可以让loss最小的$\omega$和$b$,我们就叫做$\omega \ast$和$b\ast$。
如何找到最佳的$\omega$和$b$呢？为了要简化起见，我们先假设我们未知的参数只有一个，就是$\omega$，我们先假设没有$b$那个未知的参数，只有$\omega$这个未知的参数。那当我们$\omega$代不同的数值的时候，我们就会得到不同的Loss，这一条曲线就是error surface。

Gradient Descent

• 那首先你要随机选取一个初始的点，那这个初始的点，我们叫做${\omega }_0$，那这个初始的点往往真的就是随机的，那在往后的课程裡面，我们其实会看到也许有一些方法，可以给我们一个比较好的${\omega }_0$的值.我们先当作都是随机的
• 那接下来你就要计算，在$\omega ={\omega }_0$的时候，$\omega$这个参数对loss的微分是多少$\partial L/\partial w|(w=w)$
• 如果导数大于0，$\omega$向左移动，反之向右移动。

那每次移动多少呢，这个步伐的大小取决于两件事：

• 这个地方的斜率有多大，如果斜率大就跨步大一点，如果斜率小就跨步小一点。
• 还有另外一个东西会影响步伐大小，这个东西我们这边用$\eta$来表示，这个$\eta$叫做learning rate，叫做学习速率，这个learning rate是你自己设定的，你自己决定这个$\eta$的大小.
  $$w_1\leftarrow w_0-\eta \frac{\partial L}{\partial w}|(w=w_0)$$
  那接下来你就是反复进行刚才的操作，你就计算一下${\omega }_1$微分的结果，然后再决定现在要把${\omega }_1$移动多少，然后再移动到${\omega }_1$，然后你再继续反复做同样的操作，不断的把$\omega$移动位置直至停下。

什么时候会停下来呢?往往有两种状况：

• 第一种状况是你失去耐心了，你一开始会设定我的上限就是设定100万次，就我参数更新100万次以后，我就不再更新了
• 还有另外一种理想上的停下来的可能是，今天当我们不断调整参数，调整到一个地方，它的微分的值就是这一项算出来正好是0的时候，参数就不会再移动位置。

推广到两个参数$\omega$和$b$，Gradient Descent方法和一个参数的时候一样：
$$w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w}|(w=w^0,b=b^0)$$
$$b^1\leftarrow b^0-\eta \frac{\partial L}{\partial b}|(w=w^0,b=b^0)$$

复杂模型的构建方式

1. Function with Unknown Parameters

简单模型的构建方式分为三部，复杂模型的构建方式和其一样，第一步还是构建一个带有未知数的Function，但这个Function要复杂的多。

现实中的问题不会这么简单，对于刚才的例子来说，Model就是一条直线，对于Linear的Model永远拟合不了复杂的变化，这是一种来自于Model的限制，我们叫Model的Bias。所以我们需要写一个更复杂，更有弹性的Function。以如下的变化为例：

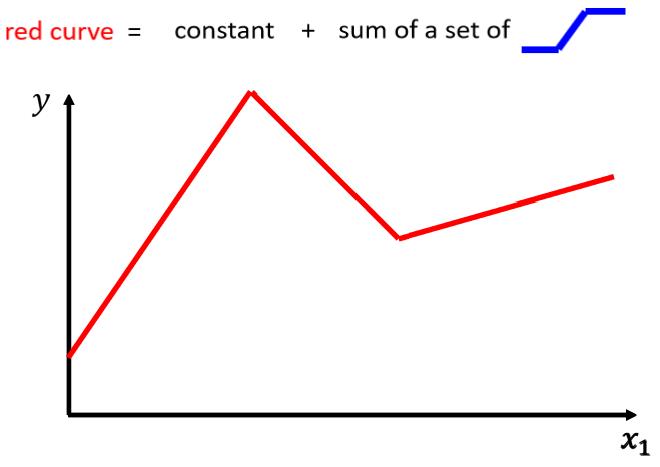
我们再定义一种新的Function：

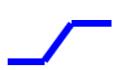
这个蓝色的 Function,它的特性是

• 当输入的值,当 x 轴的值小於某一个这个 Flash Hold 的时候,它是某一个定值,
• 大于另外一个 Flash Hold 的时候,又是另外一个定值,
• 中间有一个斜坡

这个红色的Function可以写成若干个蓝色的Function加在一起（可能会再加一个常数）：

通过上面一种组合，可以发现任何Piecewise Linear Curves都可以写成若干个蓝色的Function相加组成的

再继续拓展，但$x$和$y$的关系不是Piecewise Linear Curves 时，也许他是这样的曲线，那我们只需再这样的曲线上先取一些点，再把这些点点起来，变成一个Piecewise Linear Curves，而这个Piecewise Linear Curves 会随着点的增多跟原来的曲线越来越逼近：

所以任何的连续的曲线都可以用 Piecewise Linear Curves去逼近，而其中的每一个 Piecewise Linear Curves又都可以用一大堆蓝色的Function表示出来，也就是说我只要有足够的Function把他们加起来就可以变成任何的曲线。

那蓝色的Function怎么表示呢，同样我们用一条曲线去逼近这个Function，这个Sigmoid Function式子用这个表示：$$y=c\frac{1}{1+e^{-(b+wx)}}$$ 可以简写$$y=c\ast sigmoid(b+wx)$$成其图像如下：

通过调整$b$，$c$，$w$可以制造任何形状的Sigmoid Function，用各种不同形状的 Sigmoid Function,去逼近这个蓝色的 Function. 所以Function都可以用统一的式子表达：$$y=b+\sum _i{c}_{i}sigmoid(b_i+w_{i}x)$$
但上面的Model尽管已经特别有弹性，仍旧存在Bias。我们之前列举的Sigmoid Function$$y=c\ast sigmoid(b+wx)$$可以看到$y$只和当前的$x$有关，但实际问题中，$y$的值可能是又多个$x$决定的，例如斐波那契数列中此项的值就和上两项有关，又或者一个简单的预测问题，下一个$y$的值是由之前7个$x$

以上是关于机器学习笔记的主要内容，如果未能解决你的问题，请参考以下文章

机器学习笔记：大话线性回归

斜率优化

机器学习笔记：Adam

斜率优化dp学习笔记

单调性优化学习笔记

动态规划专题——斜率优化DP