算法日练-最长公共前缀

Posted 2022-04-21 涤生大数据

1 题目

1.1 题目描述

给你一个大小为 n 的字符串数组 strs ，其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长
公共前缀，返回这个公共前缀。

原题链接：https://leetcode-cn.com/problems/longest-common-prefix/

示例

输入：str1 = [“flower”,“flow”,“flight”]
返回值：“fl”
输入：str2 = ["abca","abc","abca","abc","abcc"]
返回值："abc"

1.2 题目分析及解答

解题思路1-遍历

求公共前缀，那我们可以从第一个字符开始，逐位比较，找到最长公共子串。
1.处理数组为空的特殊情况。
2.因为最长公共前缀的长度不会超过任何一个字符串的长度，因此我们逐位就以第一个字符串为标杆，遍历第一个字符串的所有位置，取出字符。
3.遍历数组中后续字符串，依次比较其他字符串中相应位置是否为刚刚取出的字符，如果是，循环继续，继续查找，如果不是或者长度不足，说明从第i位开始不同，前面的都是公共前缀。
4.如果遍历结束都相同，最长公共前缀最多为第一个字符串。

该思路存在两种遍历方式：

1.横向
2.纵向

横向：

步骤：

1.首先确定第i个与第i+1个字符串子串相同的公共前缀K。
2.将上面找到的前缀K与第i+2个子串进行对比，得到他们的公共前缀K1
3.重复上述步骤，最终得到字符串的最长公共前缀

package string;

public class IDEA_1 

    public static  void main(String[] args)
        String[]str1 = "abca","abc","abca","abc","abcc";
        System.out.println("最长公共前缀：" + longestCommonPrefix(str1));
    

    public static String longestCommonPrefix(String[] strs) 
        //若未遍历完所有的是字符串时最长公共前缀已经是空串，则返回""
        if (strs == null || strs.length == 0) 
            return "";
        
        int length = strs[0].length();
        int count = strs.length;
        for (int i = 0; i < length; i++)
        
            char c = strs[0].charAt(i);
            for (int j = 1; j < count; j++) 
                if (i == strs[j].length() || strs[j].charAt(i) != c) 
                    return strs[0].substring(0, i);
                
            
        
        return strs[0];
    

复杂度分析

时间复杂度：O(M*N) 其中 M 是字符串数组中的字符串的平均长度，N是字符串的数量。最坏情况下，字符串数组中的每个字符串的每个字符都会被比较一次；

空间复杂度：O(1) 常数空间的复杂度

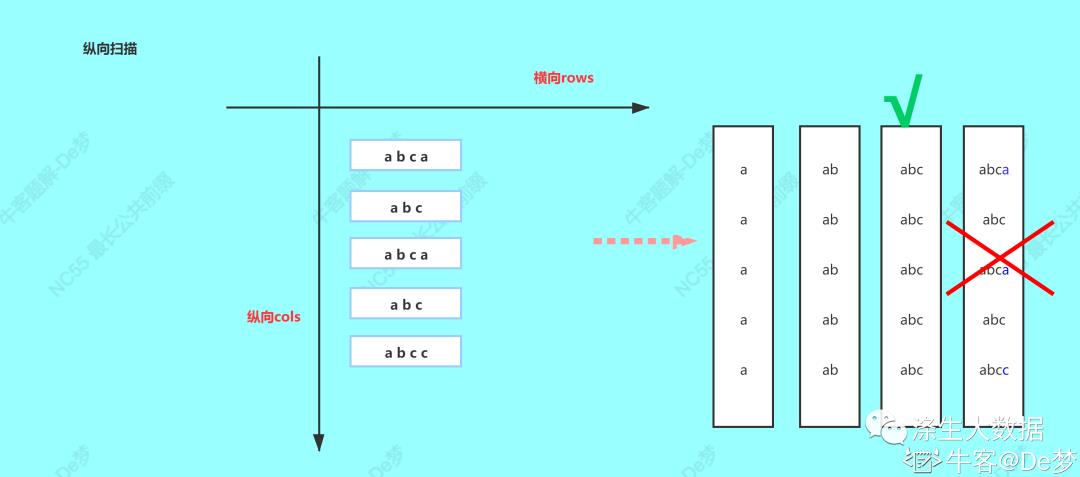
纵向

前往后依次遍历所有字符串的每一列，比较相同列上的字符是否相同，如果说相同则继续对下一列进行比较，如果说不想同则当前列不再属于公共前缀，当前列之前的部分为最长公共前缀

package string;

public class IDEA_2 

    public static  void main(String[] args)
    
        String[]str1 = "abca","abc","abca","abc","abcc";
        System.out.println("最长公共前缀：" + longestCommonPrefix(str1));
    

    public static String longestCommonPrefix(String[] strs) 
        if(strs == null || strs.length == 0) 
            return "" ;
        
        int length = strs[0].length();
        int count =strs. length ;
        for(int i = 0; i < length; i++)
            char c = strs[0]. charAt(i) ;
            for( int j =1; j < count; j++) 
                if(i == strs[j].length()||strs[j].charAt(i) != c)
                    return strs[0]. substring(0,i) ;
                
            
        
        return strs[0] ;
    

复杂度分析

时间复杂度和空间复杂度均和横向一致！

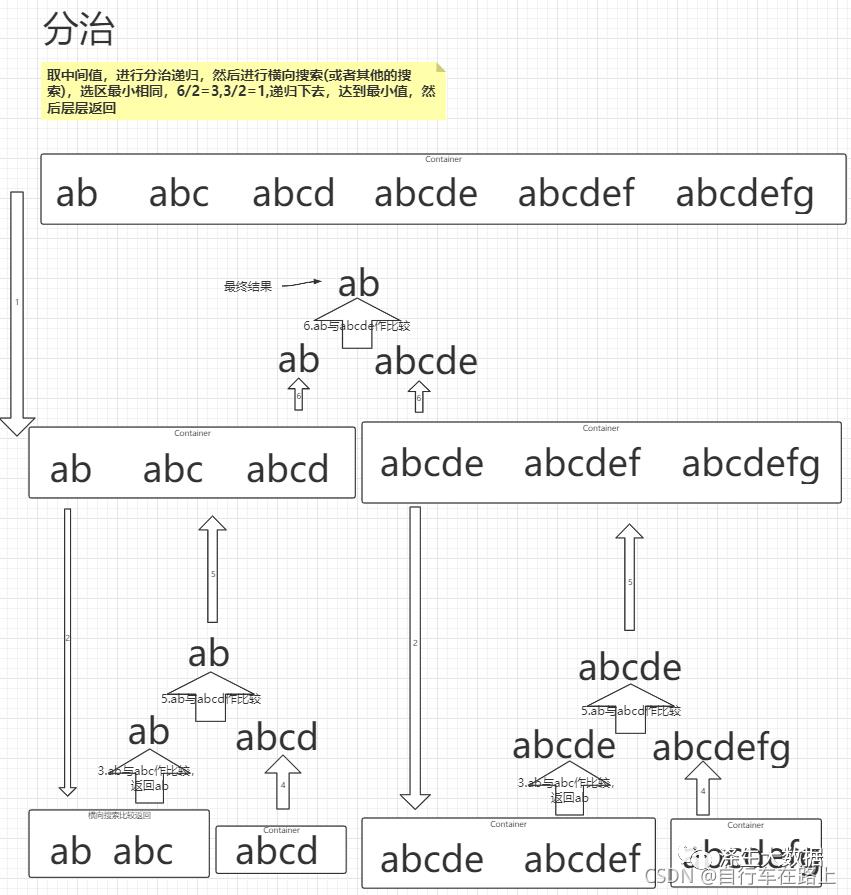
解题思路2-分治

思路：注意到 LCP 的计算满足结合律，有以下结论：
LCP(S1…Sn)=LCP(LCP(S 1…Sk),LCP(Sk+1…Sn))

其中 LCP(S1…Sn) 是字符串 S1…Sn的最长公共前缀，1 < k < n。
基于上述结论，可以使用分治法得到字符串数组中的最长公共前缀。对于问题 LCP(Si⋯Sj)，可以分解成两个子问题 LCP(Si…Smid) 与 LCP(Smid+1…Sj)，其中 mid= (i+j) / 2。对两个子问题分别求解，然后对两个子问题的解计算最长公共前缀，即为原问题的解。

public class IDEA_3 

    public static  void main(String[] args)
        String[]str1 = "abca","abc","abca","abc","abcc";
        System.out.println("最长公共前缀：" + longestCommonPrefix(str1));
    

    //分治法

    public static String longestCommonPrefix(String[] strs) 
        if ( strs.length==0 || strs==null ) 
            return "";
        
        return divide(strs, 0, strs.length-1);

    
    public static String divide(String[] s, int left, int right) 
        if ( left==right) return s[left];
        int mid = (left+right)/2;
        String s1 = divide(s, left, mid);
        String s2 = divide(s, mid+1, right);
        return Prefix(s1, s2);

    
    public static String Prefix(String s1, String s2) 
        int length = Math.min(s1.length(), s2.length());
        int index=0;
        for ( int i=0; i<length; i++ ) 
            if ( s1.charAt(i)!= s2.charAt(i) ) 
                break;
            
            index++;
        
        return s1.substring(0, index);
    

复杂度分析

时间复杂度O(MN)：其中 m 是字符串数组中的字符串的平均长度，n 是字符串的数量。二分查找的迭代执行次数是 O(logm)，每次迭代最多需要比较 mn个字符，因此总时间复杂度是O(mnlogm)。

空间复杂度O(MlogN)：其中 m 是字符串数组中的字符串的平均长度，n 是字符串的数量。空间复杂度主要取决于递归调用的层数，层数最大为 logn，每层需要 m 的空间存储返回结果

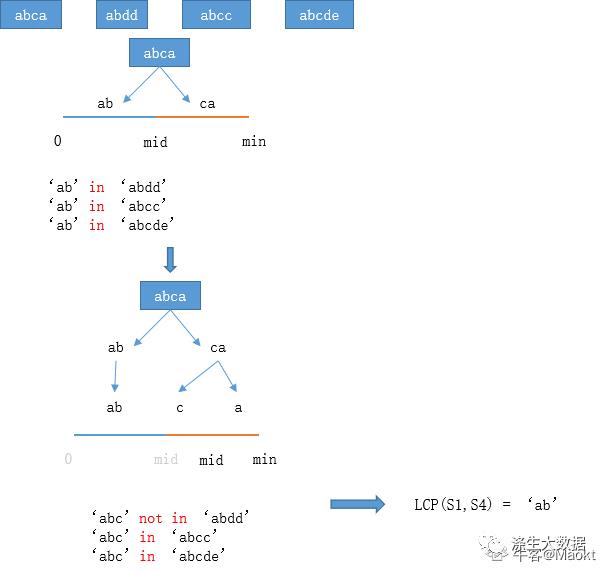
解题思路3-二分查找

思路：最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。用 minLength 表示字符串数组中的最短字符串的长度，则可以在 [0,minLength] 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 mid，判断每个字符串的长度为 mid 的前缀是否相同，如果相同则最长公共前缀的长度一定大于或等于 mid，如果不相同则最长公共前缀的长度一定小于 mid，通过上述方式将查找范围缩小一半，直到得到最长公共前缀的长度。

package string;
import java.util.*;


public class IDEA_4 

    public static  void main(String[] args)
        String[]str1 = "abca","abc","abca","abc","abcc";
        System.out.println("最长公共前缀：" + longestCommonPrefix(str1));
    

    //二分查找
    public static String longestCommonPrefix (String[] strs) 
        // write code here
        if (strs == null || strs.length == 0) 
            return "";
        
        int minLength = Integer.MAX_VALUE;
        for (String str : strs) 
            // 获取最短字符串的长度
            minLength = Math.min(minLength, str.length());
        
        // 二分查找
        int low = 0, high = minLength;
        while (low < high) 
            // 分别对前后两部分进行判断
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) 
                low = mid;
             else 
                high = mid - 1;
            
        
        return strs[0].substring(0, low);
    
    // 判断长度为 length 的字符是否是strs的共同字串
    public static boolean isCommonPrefix(String[] strs, int length) 
        String str0 = strs[0].substring(0, length);
        int count = strs.length;
        for (int i = 1; i < count; i++) 
            String str = strs[i];
            for (int j = 0; j < length; j++) 
                if (str0.charAt(j) != str.charAt(j)) 
                    return false;
                
            
        
        return true;
    

复杂度分析

时间复杂度O(MNlogM)：其中 m 是字符串数组中的字符串的平均长度，n 是字符串的数量。二分查找的迭代执行次数是 O(logm)，每次迭代最多需要比较 mn个字符，因此总时间复杂度是O(mnlogm)。 空间复杂度O(1)：使用的额外空间复杂度为常数。

参考

1.https://www.nowcoder.com/practice/28eb3175488f4434a4a6207f6f484f47?tpId=295&tqId=732&ru=/exam/oj&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Foj

2.https://blog.csdn.net/llhwx/article/details/107448032