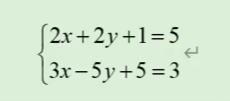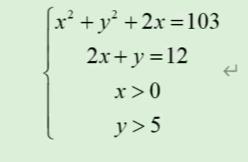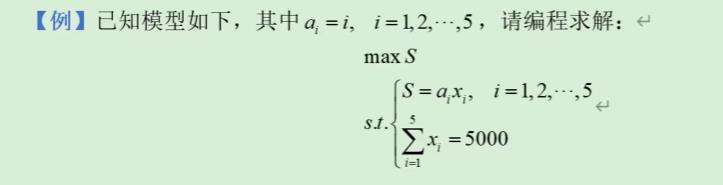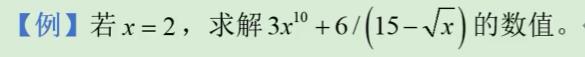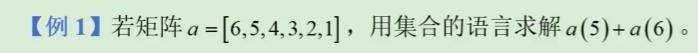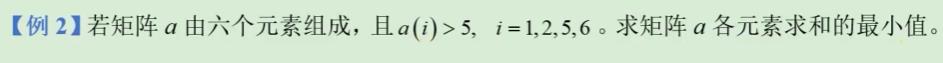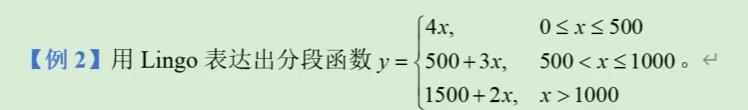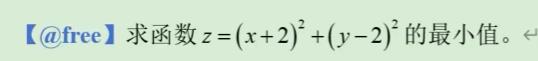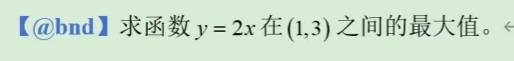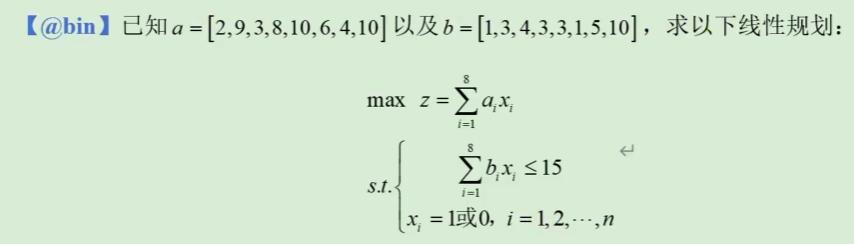备战数学建模8-LINGO从入门到熟练掌握

Posted 2022-04-18 nuist__NJUPT

目录

一、Lingo解方程

二、lingo变量

三、线性规划基础

四、集合vs矩阵工厂

1-矩阵工厂

2-工厂合并

五、运算符&内置函数

1-算术运算符

 2-关系运算符

3-逻辑运算符

4-内置函数

---

一、Lingo解方程

LINGO对于求解线性规划问题较为容易，俗称优化神器，我们学习一下是使用LINGO编程解方程。

我们看一下上面的一元二次方程，求解出的x=1,y=1，lingo代码如下所示：

2*x + 2*y + 1 = 5 ;
3*x - 5*y + 5 = 3 ;

我们在求解一下上面的方程组，代码如下所示：

x^2 + y^2 + 2*x = 103 ;
2*x + y  = 12 ;
y > 5;
x > 0 ; !这一行不写也是可以的，lingo默认所有变量大于等于0;

二、lingo变量

1-Lingo默认所以变量为大于等于0的数字，因而非负的条件不必多写。

2-如果遇到一个变量小于0，要使用@free函数使其定义域为R。

3-Lingo不区分大小写，对于M和m是等价的，所以建议在lingo中尽量都使用小写字母。

4-变量命名规范，使用字母，数字，下划线，且字母打头。

三、线性规划基础

1-一个线性规划只含有一个目标函数(两个以上的是多目标线性规划，lingo无法直接求解)

2-求目标函数的最大值和最小值分别用max=...或min=...来表示。

3-以!开头,并以;结尾的是lingo的注释

4-线性规划和非线性规划的本质区别是目标函数是否线性，其余一致，故不需要去区分，但需要注意的是非线性规划的求解很困难，基本得不到全局最优解。

我们看一下上面的这个线性规划的例子，使用lingo求解此类问题比较方便。通过上面的例子，我们可以列出一个数学模型，如下所示：

计算结果为x1=100, x2=30, 目标值是29000，lingo代码如下所示：

max = 200*x1 + 300*x2 ;
x1 <= 100 ;
x2 <= 120 ;
x1 + 2*x2 <= 160 ;

四、集合vs矩阵工厂

1-矩阵工厂

我们首先看一下上面的这个例子，求出的结果如下目标值是S=2189.781，我给出的lingo暴力枚举的代码如下：

max = s ;
a1 = 1 ;
a2 = 2 ;
a3 = 3 ;
a4 = 4 ;
a5 = 5 ;
s = a1*x1 ;
s = a2*x2 ;
s = a3*x3 ;
s = a4*x4 ;
s = a5*x5 ;
x1 + x2 + x3 + x4 + x5 = 5000 ;

我们看一下下面的这段代码，做进一步的分析。(不必在意空格，lingo不读取空格)

1-factory和plant都是制造矩阵的工厂，但是它们是两家不同的工厂。

2-factory后面的/1..6/说明它专门生成1×6的矩阵。factory后面出现的a,b都是1×6的矩阵。

3-plant后面的/1..3/说明它专门生产1×3的矩阵，plant后面的x,y都是1×3的矩阵。

4-矩阵工厂的名字factory是随便起的，工厂所生产的矩阵的名字a,b也是随便起的。

5-上面的代码只是定义了四个矩阵的大小，矩阵工厂只是中介。

6-生产完矩阵之后，工厂和矩阵将脱开联系。

7-LINGO不是一行一行读代码的，所以用sets和endsets表示矩阵生产流程的起始与终止。

生产完矩阵之后，我们需要为矩阵赋初值，如下生成

sets:
factory /1..6/ : a,b ;
plant /1..3/ : c,x ;
endsets

data:
a = 1,2,3,4,5,6 ;
b = 6,5,4,3,2,1 ;
c = 10,20,30 ;
enddata

以上程序对应以下知识点：

1-不是每个矩阵都要赋值，有些矩阵式我们要求解的变量。

2-需要赋值的矩阵必须赋满。

3-lingo中可以给矩阵赋值小数，也可以给矩阵赋值整数。不能赋值分数。

4-lingo不是一行一行读代码的，而是用data:和enddata表示矩阵的起止。

我们现在再看一下上面的例子，利用矩阵工厂和for循环，以及sum函数完成求解，代码如下：

model:
sets:
gc /1..5/ : a,x ;
endsets

data:
a = 1,2,3,4,5 ;
enddata

max = s ;
@for(gc(i) : s = a(i) * x(i)) ; 
@sum(gc(i) : x(i)) = 5000 ;
end

2-工厂合并

我们看一下上面的例子，就是矩阵合并，首先使用矩阵工厂分别生成1行6列的矩阵a和1行8列的矩阵d，那么生成的c和x都是6行8列的矩阵。

我们看一下上面的例子，编程求解上面的线性规划模型，求出来的目标值是664，lingo代码如下所示：

model:
sets:
factory /1..6/ : a ;
plant /1..8/ : d ;
coo (factory,plant) : c, x ;
endsets

data:
a = 60, 55, 51, 43, 41, 52 ;
d = 35, 37, 22, 32, 41, 32, 43, 38 ;
c = 6, 2, 6, 7, 4, 2, 5, 8
    4, 9, 5, 3, 8, 5, 8, 2 
    5, 2, 1, 9, 7, 4, 3, 3 
    7, 6, 7, 3, 9, 2, 7, 1
    2, 3, 9, 5, 7, 2, 6, 5 
    5, 5, 2, 2, 8, 1, 4, 3;

enddata

min = @sum(coo(i,j) : c(i,j) * x(i,j)) ;
!min = @sum(factory(i) : @sum(plant(j) : x(i,j) * c(i,j))) ;
@for(factory(i) : @sum(plant(j) : x(i,j)) <= a(i)) ;
@for(plant(j) : @sum(factory(i) : x(i,j)) = d(j)) ;
@for(factory(i) : @for(plant(j) : x(i,j) >= 0)) ; !这一句可以不写;
end

五、运算符&内置函数

1-算术运算符

我们看一下上面的例子，lingo代码如下所示。

model:
x = 2 ;
y = 3*x^10 + 6/(15-@sqrt(x)) ;
end

 2-关系运算符

1-关系运算符用在约束条件中，指定约束条件两边必须满足的条件。

2-严格意义上说，lingo只有三种关系运算符，即>=,<=,=.

3-逻辑运算符

lingo的逻辑运算符可以参考如下表格。

逻辑运算符出现的位置：1-for循环与sum求和，2-if判断

我们看一下上面的例子1，求解的结果是3，代码如下所示：

model:

sets:
factory /1..6/ : a ;
endsets

data:
a = 6,5,4,3,2,1 ;
enddata
y = @sum(factory(i) | i#ge#5 : a(i)) ;
end

我们看一下上面的例子2，目标值等于20，代码如下所示：

model:

sets:
factory /1..6/ : a ;
endsets

min = @sum(factory(i) :  a(i)) ;
@for(factory(i) | i#le#2 #or# i#ge#5 : a(i) > 5 ) ;
end

我们继续看一下上面的例子3，结果为26， 具体的lingo代码如下所示：

model:

sets:
fac /1..3/ : ;
coo (fac, fac) : a ;
endsets

data:
a = 1,2,3
    4,5,6
    7,8,9 ;
enddata
y = @sum(coo(i,j) | j#ge#i : a(i,j)) ;
end

4-内置函数

我们看一下上面的例子1，由于lingo代码默认所有变量大于等于0，故我们应该首先让其自由化，即让其定义域为R，if函数语法简单，看一眼就能学会。

具体的lingo代码如下所示：

model:
@free(x) ;
@free(y) ;

x = -10 ;
y = @if(x#ge#0, x+10, x-10) ;
end

我们再看一下上面的例子2，这个分段函数分为三段，具体的lingo代码如下所示：

model:
x = 1500 ;
y = @if(x#le#500, 4*x, @if(x#gt#1000, 1500+2*x, 500+3*x));

end

变量定界函数如下表所示，主要记住4个。

我们看一下上面的例子，Lingo代码如下所示。

model:
@free(x) ;
@free(y) ;
min = (x+2)^2 + (y-2)^2 ;
end

 

我们看一下上面使用内置函数@bnd的例子，lingo代码如下所示。

model:
@bnd(1,x,3) ;
max = 2 * x ;
end

我们看一下上面的使用内置函数@bin的例子，求出的目标值是38，lingo代码如下所示。

model:
sets:
fac /1..8/ : a, b, x ;
endsets

data:
a = 2,9,3,8,10,6,4,10 ;
b = 1,3,4,3,3,1,5,10 ;
enddata
max = @sum(fac(i) : a(i) * x(i)) ;
@sum(fac(i) : b(i) * x(i)) <= 15 ;
@for(fac(i) : @bin(x(i))) ;
end

我们看一下使用@bin函数求整数规划问题，lingo代码如下所示。

model:
sets:
factory /1..6/ : a, x ;
plant /1..5/ : b ;
coo (factory,plant) : c ;
endsets

data:
a = 2.1 1.0 1.8 1.2 2.0 1.2 ;
b = 6 125 12500 345 5 ;
c = 0.45 20 415 22 0.3 
    0.45 28 4065 5 0.35
    0.65 40 850 43 0.6
    0.4 25 75 27 0.2
    0.5 26 76 48 0.4
    0.5 75 235 8 0.6 ;
enddata
max = @sum(factory(i) : a(i) * x(i)) ;
@for(plant(j) : @sum(factory(i) : c(i,j)*x(i)) <= b(j)) ;
@sum(factory(i) : x(i)) = 14 ;
x(2) <= 3 ;
x(4) <=2 ;
@for(factory(i) | i#ne#2 #and# i#ne#4 : @bnd(1,x(i),4)) ;
@for(factory(i) : @gin(x(i))) ;
end

LINGO中提供了数学函数，常用的如下表所示：

 

我们看一下上面的例子1，代码如下所示。

model:
y = @sin(3.14159) + @log(1024) / @log(2) + @abs(-10) + @exp(0) ;
end

lingo中提供了集合操作函数，常见的有如下几个，如下表所示：

我们通过一段代码熟悉以下上面的函数吧，lingo代码如下所示。

model:
sets:
factory /1..6/ : a ;
endsets

data:
a = 1,2,3,4,5,6 ;
enddata
prod = @prod(factory(i) : a(i)) ;
greater = @max(factory(i) : a(i)) ;
less = @min(factory(i) : a(i)) ;
in = @in(factory,5) ;
size = @size(factory) ;
end