进入Computer Vision世界 —— 数字图像 + 插值算法 + 直方图 + 卷积&滤波

Posted 2022-04-16 ErrorError！

进入Computer Vision世界 —— 数字图像 + 插值算法 + 直方图 + 卷积&滤波

目录

• • 进入Computer Vision世界 —— 数字图像 + 插值算法 + 直方图 + 卷积&滤波
  • 1. 数字图像
  • • 1.1 图像基础
    • • 1.1.1 像素、灰度与对比度
      • 1.1.2 RGB颜色模型
      • 1.1.3 频率与赋值
    • 1.2 图像的取样与量化
  • 2. 插值算法
  • • 2.1 最邻近插值 The nearest interpolation
    • 2.2 双线性插值
  • 3. 直方图、滤波和卷积
  • • 3.1 直方图
    • • 3.1.1 了解直方图及其性质和应用
      • 3.1.1 直方图均衡化
    • 3.2 滤波和卷积
    • • 3.2.1 滤波与卷积的基本原理
      • 3.2.2 卷积——过滤器 / 卷积核（Kernel）
      • 3.2.3 卷积核的应用
      • 3.2.4 卷积本身的计算

1. 数字图像

1.1 图像基础

关于图像，我们最常听说的就是图像的像素，那么像素到底是什么？它的取值又意味着什么？我们一起来聊一聊，通过这一篇文章大概了解一些关于计算机视觉的术语，在脑海中对计算机视觉留下一个印象方便我们的持续学习

数字图像：计算机保存的图像本质上都是一个一个的像素点，这些像素点就称为数字图像

1.1.1 像素、灰度与对比度

像素，一个很简单却意义重大的词汇，像素是分辨率的单位，是构成位图图像最基本的单元，每一个像素都有自己的颜色，这些一个一个的像素组成了我们五花八门的图像，分辨率也叫解析度，图像的分辨率就是单位英寸内的像素点数（单位为PPI），PPI表示每英寸对角线上所拥有的像素数目

关于图像有三个非常重要的名词：灰度、通道和对比度

灰度表示图像像素明暗程度的数值，也就是黑白图像中点的颜色深度，灰度图是怎么来的呢？它是对图像的通道做了修改才显示出黑白灰的视觉效果，通道即颜色通道，它将图像分解成一个或多个颜色成分

• 单通道：一个像素点只需要一个数值表示，只能表示灰度（0为黑色255为白色）

• 三通道：又称RGB模式，把图像分为红绿蓝三个通道，可以表示彩色

• 四通道：在三通道RGB的基础上加了一个透明度alpha通道，当它为0时表示全透明

对比度也是数字图像中相当重要的一个概念，它指不同颜色之间的差别，对比度=最大灰度值/最小灰度值

我们了解了什么是颜色通道后，其中最常用的一种RGB模型也是需要我们仔细了解一下的，色彩三原色指的是品红+黄+青，而我们所说的RGB模型的三种颜色是光学三原色，其中包括红+绿+蓝

1.1.2 RGB颜色模型

RGB颜色模型

RGB颜色模型指的是三维直角坐标系颜色系统中的一个单位正方体，在正方体的对角线上，各原色的量相等，产生由暗到亮的白色，即灰度，正方体的其他6个角点分别为红、黄、绿、青和品红

RGB值转化为浮点数：浮点数运算结果更加精确，整数运算过程中会因丢失小数部分可能导致颜色值严重失真

注意：关于颜色模RBG这一方面有一个OpenCV的大坑，OpenCV对于读进来的图片的通道排列是BGR而不是RGB

# 由于在OpenCV中使用imread()方法读入的图像是BGR通道，我们怎么把它转为RGB通道
img = cv.imread('test.png')
img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

1.1.3 频率与赋值

图像的频率和幅值也是很常用的两个概念，所谓频率指的就是灰度值变化的剧烈程度，是灰度在平面空间上的梯度，而幅值是在一个周期内，交流电噬魂师出现的1最大绝对值，这也是一个正弦波，波峰到波谷的距离的一般

1.2 图像的取样与量化

我们在前面说过，计算机保存图像是通过一个一个的像素点保存的，这些像素点就是数字图像，但是我们怎么把一个图像数字化，即转化为一个一个的像素点呢，这就涉及到了图像的取样与量化

取样：要用多少点来描述一幅图像，取样结果质量的高低就是用图像的分辨率来衡量的

量化：指要使用多大范围的数值来表示图像采样后的一个点

数字化坐标值称为取样，数字化幅度称为量化

所谓上采样与下采样说的就是缩小图像和放大图像：

下采样（缩小图像）是为了使得图像符合显示区域的大小或生成对应图像的缩略图，而上采样（放大图像 / 图像插值）的主要目的是放大原图像使其可以显示在更高分辨率的显示设备上

2. 插值算法

什么是插值，比如说我们要放大一个有100个图像，单纯的拉伸图像会使图像的分辨率降低，怎么使它的分辨率不降低或者尽量不降低呢？那就要插入一些新的像素点，使得一个有100个像素点的图像放大到十倍，使它有1000个像素点，这就解决了失真和分辨率降低的问题，这些新增的像素点从哪来，它的像素值是多少，怎么插？这就是我们的插值算法要做的事情，这里我们介绍几种常用的插值方法

2.1 最邻近插值 The nearest interpolation

我们通过一个例子来说明最邻近插值算法的实质，比如说我们需要放大的图像img1的左上角有四个相邻的像素点，在图像放大后我们要在这四个像素点之间加入一些新的像素点，这些新点的像素值的确定，取决于它落在的位置

设i+u, j+v (i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v) 取决于它的位置

关于最邻近插值的算法的代码实现我们敲一敲理解一下，比如我们将一个原本400 * 400的图像放大到800 * 800，这多出来的像素就有最邻近插值算法来完成

import cv2
import numpy as np
# 定义一个函数，用来实现算法
def function(img):
    # 这三个值分别是高、宽和通道数（ing.shape返回的是一个三元组的值）
    height,width,channels =img.shape
    emptyImage=np.zeros((800,800,channels),np.uint8)
    sh=800/height
    sw=800/width
    for i in range(800):
        for j in range(800):
            x=int(i/sh)
            y=int(j/sw)
            emptyImage[i,j]=img[x,y]
    return emptyImage
 
img=cv2.imread("lenna.png")
zoom=function(img)
print(zoom)
print(zoom.shape)
cv2.imshow("nearest interp",zoom)
cv2.imshow("image",img)
cv2.waitKey(0)

代码解析：在python中，关于图像处理我们需要了解几个极具代表性的第三方库numpy、matplotlib和opencv-python等，他们提供了很多方法来协助我们实现操作，第7行代码的np.zeros()是numpy提供的方法，它返回的是一个给定形状和类型，且用0填充内容的数组，在图像处理在一方面我们可以理解为它创建了一个空的画布，这个画布在本例中是800x800大小的，我们用像素点将其填充完毕，它就变成了数字图像，将其显示就实现了我们方法图像的需求

两个嵌套的for循环（图像是2维的）就是我们实现插值的关键代码，我们依次遍历这800x800的每一个像素点，那我们怎么确定这个点应该填充什么值呢？我们上面说这个值的确定是由它落入的位置决定的，就是说我们要把这个800x800的图像再放回400x400的图像中，去确定它的位置，第7、8行我们求了放大比例，将这个比例用在第12、13行，就是用大图的像素位置去除这个比例，就得到了在小图中这个点的位置，将其强转为int类型，它就与原图像中的某个坐标的像素值保持，这就达成了我们为新增像素点赋值的操作

2.2 双线性插值

在学习双线性插值之前我们先看看单线性插值，在单线性插值的过程中我们已知两个点的坐标，那就等于得到了通过了这两个点的直线的方程，于是我们就能得到这个线段上所有点的坐标了

比例换算：y = [(x1-x)/(x1-x0) ]*y0 + [(x-x0)/(x1-x0)]y1

双线性插值其实就是两次单线性插值

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-10DTbxAI-1649816773458)(OpenCV%E7%AC%94%E8%AE%B0/image-20220412130627741.png)]

具体过程：由Q12和Q22做一次单线性插值得到R2，再由Q11和Q21用同样的方法求得R1，得到R1和R2后再对这两个点做一次单线性插值得到我们需要的P点，这个时候再使用最邻近插值就能确定P像素点的取值了

上代码大家感受一下这个算法的实现过程

import numpy as np
import cv2
  
'''
python implementation of bilinear interpolation
'''
def bilinear_interpolation(img,out_dim):
    src_h, src_w, channel = img.shape
    dst_h, dst_w = out_dim[1], out_dim[0]
    print ("src_h, src_w = ", src_h, src_w)
    print ("dst_h, dst_w = ", dst_h, dst_w)
    if src_h == dst_h and src_w == dst_w:
        return img.copy()
    dst_img = np.zeros((dst_h,dst_w,3),dtype=np.uint8)
    scale_x, scale_y = float(src_w) / dst_w, float(src_h) / dst_h
    for i in range(3):
        for dst_y in range(dst_h):
            for dst_x in range(dst_w):
  
                # find the origin x and y coordinates of dst image x and y
                # use geometric center symmetry
                # if use direct way, src_x = dst_x * scale_x
                src_x = (dst_x + 0.5) * scale_x-0.5
                src_y = (dst_y + 0.5) * scale_y-0.5
  
                # find the coordinates of the points which will be used to compute the interpolation
                src_x0 = int(np.floor(src_x))
                src_x1 = min(src_x0 + 1 ,src_w - 1)
                src_y0 = int(np.floor(src_y))
                src_y1 = min(src_y0 + 1, src_h - 1)
  
                # calculate the interpolation
                temp0 = (src_x1 - src_x) * img[src_y0,src_x0,i] + (src_x - src_x0) * img[src_y0,src_x1,i]
                temp1 = (src_x1 - src_x) * img[src_y1,src_x0,i] + (src_x - src_x0) * img[src_y1,src_x1,i]
                dst_img[dst_y,dst_x,i] = int((src_y1 - src_y) * temp0 + (src_y - src_y0) * temp1)
  
    return dst_img
  
  
if __name__ == '__main__':
    img = cv2.imread('lenna.png')
    dst = bilinear_interpolation(img,(700,700))
    cv2.imshow('bilinear interp',dst)
    cv2.waitKey()

双线性插值法的计算比最邻近插值法更复杂，计算量也很庞大，但没有灰度不连续的缺点，图像会看起来更光滑

关于双线性插值会存在的问题——坐标系的选取

如果源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：

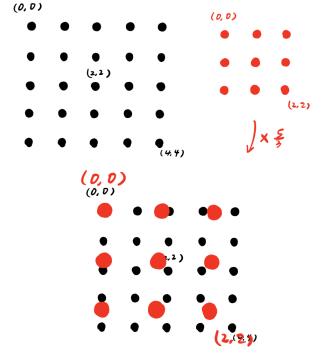
这样得出的结果会有一定的误差，所以我们需要更改坐标系的选取，那就是使几何中心重合（所有坐标加0.5），使所有的点都参与计算

3. 直方图、滤波和卷积

3.1 直方图

3.1.1 了解直方图及其性质和应用

在图像处理中直方图也是一个相当重要的概念，灰度直方图描述了图像中灰度分布情况，能够很直观地展示出图像中各个灰度级别所占的多少，总的来说它就是关于灰度级的一个函数，描述了图像中具有某个灰度级的像素个数，横坐标是灰度级，纵坐标是该灰度级出现的频率

关于直方图大家很容易有一个误解，那就是会不清楚像素的空间位置与直方图之间的关系是什么，他们之间的关系只有一个——他们没有关系！图像直方图是不关心像素点的空间位置的，因此不受图像旋转和平移变化的影响，可以作为图像的一个特征

任何一副特定的图像都与唯一的直方图与之对应，但不同的图像可以有相同的直方图，如果一幅图像有两个不相连的区域组成，并且每个区域的直方图已知，则整幅图像的直方图是该两个区域的直方图之和

直方图的应用：通过直方图我们可以了解整个图像的明暗概况的概况

3.1.1 直方图均衡化

直方图均衡化是将原图像的直方图通过变换函数变为均匀的直方图，然后按均匀直方图修改原图像，从而获得一幅灰度分布均匀的新图像，直方图的均衡化就是使用某种算法使直方图大致平和的方法，它的作用是图像增强（提升对比度）

将一个像素值分布不均匀的图像变成一个像素值分布相对均匀的图像

为了将原图像的亮度范围进行扩展，需要一个映射函数，将原图像的像素值均衡映射到新直方图中，这个映射函数有两个条件：1.为了不打乱原有的顺序，映射后明暗的大小关系不能改变；2.映射后的的图像像素值必须在原有的范围内；

均衡化的算法有几个主要的步骤：

1. 依次扫描原始灰度图像的每一个像素，计算出图像的灰度直方图
2. 计算灰度直方图的累加直方图
3. 根据累加直方图和直方图均衡化原理得到输入与输出之间的映射关系
4. 最后根据映射关系得到结果：dst(x,y) = H’(src(x,y))进行图像变换

均衡过程详解：

---

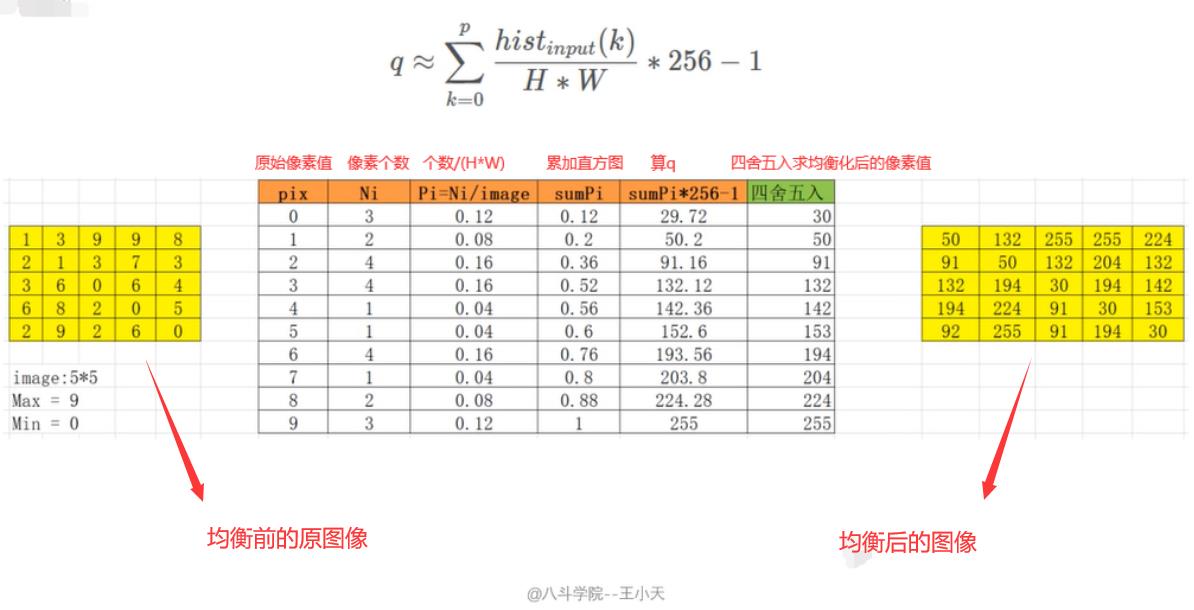
在实际开发中我们使用opencv的接口即可，但是直方图均衡化的过程我们要了解

3.2 滤波和卷积

3.2.1 滤波与卷积的基本原理

线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果，卷积的原理与滤波类似，但是卷积有着细小的差别，卷积操作也是卷积核与图像对应位置的乘机和，但是卷积操作在做乘积之前需要先将卷积核翻转180度（卷积用符号*表示）

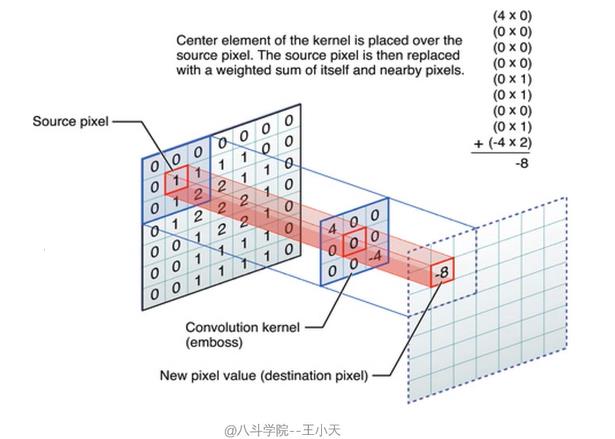
卷积与滤波是不同的两个概念，并不是说卷积是由滤波推导而来的，二者在使用时就已经是最终形态了不需要额外的操作，只有在对滤波和卷积进行转化操作时在会加上一个卷积核翻转180度的操作

3.2.2 卷积——过滤器 / 卷积核（Kernel）

卷积核就是图像处理时，给定输入图像，输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核

对于卷积核是有一定的规则要求的：

1. 滤波器的大小应该是奇数，这样它才有一个中心，例如3x3，5x5或者7x7，卷积核有了中心有中心了，也有了半径的称呼，例如5x5大小的核的半径就是2
2. 滤波器矩阵所有的元素之和应该要等于1，这是为了保证滤波前后图像的亮度保持不变。但这不是硬性要求
3. 如果滤波器矩阵所有元素之和大于1，那么滤波后的图像就会比原图像更亮，反之，如果小于1，那么得到的图像就会变暗。如果和为0，图像不会变黑，但也会非常暗
4. 对于滤波后的结构，可能会出现负数或者大于255的数值。对这种情况，我们将他们直接截断到0和255之间即可。对于负数，也可以取绝对值

在实际开发中我们会设计多种卷积核，而使用不同的卷积核处理的图像就会得到不同的效果，所有我们可以认为，不同的卷积核就代表了不同的图像模式，卷积在提取边缘方面非常的好用，提取边缘也就提取了特征，它就是我们后面学习的基石

若某个图像与此卷积核卷积出的值比较大，则认为这个图像十分接近于此卷积核

3.2.3 卷积核的应用

平滑均值滤波

在平滑均值滤波的应用实例中，待处理的图像一般会有很多的噪点（高频信号），它们与周围像素的差别比较大，使得图像看起来麻麻的并不平滑，所以我们使用一个3x3的卷积核来对图像进行卷积，这个3x3的矩阵的每一个元素都是1/9，在进行卷积后（噪点对应的像素点会被”溶解”）整个图像都看起来更平滑了（更模糊了）

高斯滤波

高斯平滑水平和垂直方向上呈高斯分布，更突出了中心点在像素平滑之后的权重，相比于均值滤波而言有着更好的平滑效果

图像锐化

图像锐化使用的是拉普拉斯变换核函数，3x3的卷积核除中心位置为9，其余位置均为-1，意在用中心像素乘9，再减去其余临近的像素值的，这就拉大了中心像素值与临近的其他像素值的差距，产生了增强图像对比度，使图像锐化的效果

Sobel边缘提取

Sobel边缘检测可以分为横向检测和纵向检测，一般来说我们会融合两种边缘提取的结果，而是横或纵取决于卷积核的使用

3.2.4 卷积本身的计算

首先我们要引入一个概念——步长，顾名思义这里的步长就代表卷积核在卷积图像时每次移动的像素个数，上面我们说到的一些例子都是每次移动一个像素然后依次改变中心像素的像素值以达到各种效果，但是我们要想每次移动s个像素呢？结果就变成了：((h-f)/s +1 , (w-f)/s + 1)

但是这会产生很多问题，如果f或步长s大于1，那么图片每次卷积后都会变小，这就会丢失很多信息，出现问题我们就要想着去解决，一般来说我们会用到一个概念——填充/Padding，最简单的一种是在外围填充一圈像素值为0的像素点，这样就会遍及每一个原像素点了，就不对出现像素点丢失的情况

卷积——三种填充方式

根据填充像素的外围圈数，我们可以分为full、same和valid三种模式，而填充圈数不同会造成什么样的影响呢？填充圈数的设置直接决定了输出图像的大小对比于原图像，是变大、不变还是变小，因为滤波器对图像进行滤波时，卷积核的中心位置决定了这个

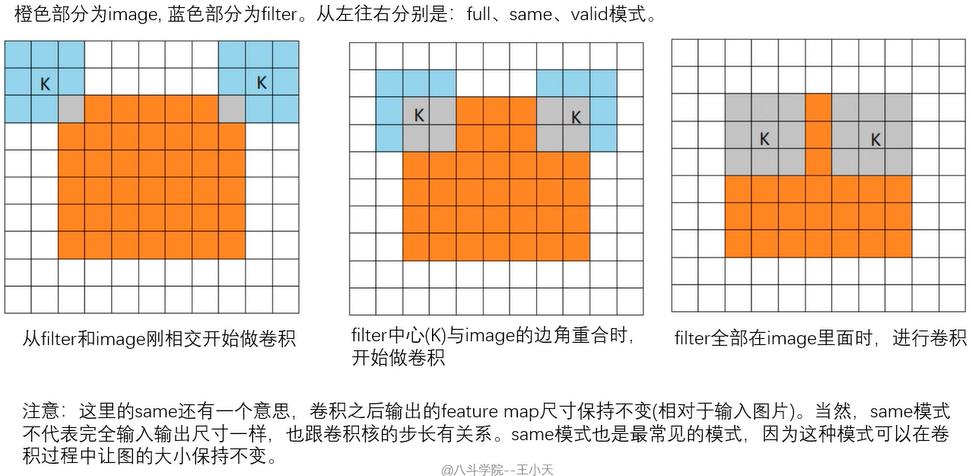
三通道卷积

三通道卷积其实就是三维的单通道卷积，相应的多通道其实就是多维的单通道卷积，对于不同的通道有着不同的卷积核（因为提取特征不一样），对于三通道图像的三通道卷积来说每一个卷积核都是3x3x3的，可以理解为单通道的卷积核是一片二维的卷积核，而三通道的卷积核是一个正方体，图中的Filter W0指的就是一整个卷积核，而Filter W1指的是另一个卷积核

图中Output Volume是卷积之后的图片，为什么7x7x2的图片变成了3x3x2的图片了呢？因为卷积的步长为2而不是1导致了这样的结果，即使已经进行了填充

对于一张图，我们可以设置n多个卷积核进行操作，在我们上述的图中，有W0和W1两个通道的输出，就是因为我们用了两个卷积核，这个时候就引出了一个相当重要的概念了，图像的输入与输出在卷积中是毫无关系的，输出是由卷积核决定的，无论是样式还是个数，都是与卷积核的类型和个数决定的

CNN（卷积神经网络）厉害的地方在于，过滤器的特征并不是人为设定的，而是通过大量图片自己训练出来的

---

版权声明：以上学习内容及配图来自或参考自——八斗人工智能
如果文章对您有所帮助，记得一键三连支持一下哦~