异常检测原理与实验

Posted 2022-04-15 普通网友

原创作品，出自 “晓风残月xj” 博客，欢迎转载，转载时请务必注明出处（http://blog.csdn.net/xiaofengcanyuexj）。

由于各种原因，可能存在诸多不足，欢迎斧正！

　　最近需要对欺诈报价进行识别处理，简单的模型就是给定很多不同数据集，需要找出每个spu下可能存在的欺诈数据，比如20,22,30,其中的欺诈数据可能就是30。其实加以抽象，属于异常检测范围。

　　异常检测是发现与大部分对象不同的对象，其中这些不同的对象称为离群点。一般异常检测的方法主要有数理统计法、数据挖掘方法。一般在预处理阶段发生的异常检测，更多的是依托数理统计的思想完成的。

一、基于模型
　　首先判断出数据的分布模型，比如某种分布（高斯分布、泊松分布等等）。然后根据原始数据（包括正常点与离群点），算出分布的参数，从而可以代入分布方程求出概率。例如高斯分布，根据原始数据求出期望u和方差？，然后拟合出高斯分布函数，从而求出原始数据出现的概率；根据数理统计的思想，概率小的可以当做离群点。

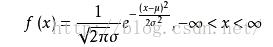
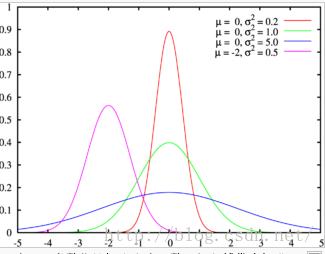
优点：

方法简单，无需训练，可以用在小数据集上。

缺点：

发现离群点效果差，离群点对模型参数影响大，造成区分效果差。需要数值化

import java.util.List;

/**
 * 实现描述：计算正态分布
 *
 * @author jin.xu
 * @version v1.0.0
 * @see
 * @since 16-9-9 下午12:02
 */
public class Gauss 
    public double getMean(List<Double> dataList) 
        double sum = 0;
        for (double data : dataList) 
            sum += data;
        
        double mean = sum;
        if (dataList.size() > 0) 
            mean = sum / dataList.size();
        
        return mean;
    

    public double getStd(List<Double> dataList, double mean) 
        double sum = 0;
        for (double data : dataList) 
            sum += (data - mean) * (data - mean);
        
        double std = sum;
        if (dataList.size() > 0) 
            std = sum / dataList.size();
        
        return Math.sqrt(std);
    

    public double getProbability(double data, double meam, double std) 
        double tmp = (1.0 / (Math.sqrt(2 * 3.141592653) * std)) * Math.exp(-(Math.pow(data - meam, 2) / (2 * Math.pow(std, 2))));
        return tmp;
    

二、基于近邻度
　需要度量对象之间的距离，离群点一般是距离大部分数据比较远的点。一般这种方法是计算每个点与其距离最近的k个点的距离和，然后累加起来，这就是K近邻方法。

　

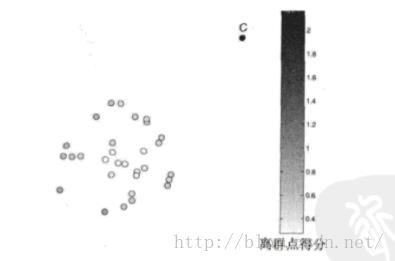
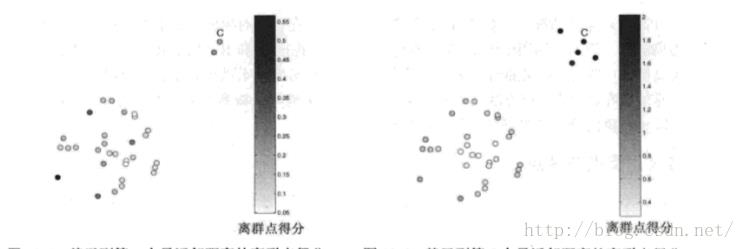
优点：

原理简单，无需训练，可用在任何数据集

缺点：

需要计算距离，计算量大，K的选定以及多于K个离群点聚集在一起导致误判。

public class KNN 
    
    public static double process(int index,Position position, int k, List<Position> positionList) 
        List<Double> distances = Lists.newArrayList();
        for (int i = 0; i < positionList.size(); ++i) 
            if (i != index) 
                distances.add(Math.sqrt(Math.pow((positionList.get(i).getX() - position.getX()), 2)+Math.pow((positionList.get(i).getY()-position.getY()),2)));
            
        
        Collections.sort(distances);
        k = k < distances.size() ? k : distances.size();

        double knnDistance = 0.0;
        for (int i = 0; i < k; ++i) 
            knnDistance += distances.get(i);
        
        return knnDistance;
    

    private static class Position
        int x;
        int y;

        public int getX() 
            return x;
        

        public void setX(int x) 
            this.x = x;
        

        public int getY() 
            return y;
        

        public void setY(int y) 
            this.y = y;
        
    

三、基于密度
　低密度区域的数据点可以当做某种程度上的离群点。基于密度的和基于近邻的是密切相关的，简单来说，密度和近邻的距离成反比。一般的度量公式如下：

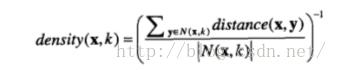
　density(x,k)表示包含x的k近邻的密度，distance(x,y)表示x到y的距离，N(x,k)表示x的k近邻集合。

优点：

相对准确

缺点：

需要度量密度，需要设定阈值


四、基于聚类
　　丢弃远离其他聚类簇的小聚类簇。需要给出小聚类簇的大小阈值、聚类簇距离阈值。常用的聚类方法比较多，比如K-means(变种K-models)、EM、层次聚类算法（分裂型和归约型）。具体方法说明可见：漫话数据挖掘。

优点：

引入数据挖掘聚类的方法，在样本充足的情况下准确度会相对较高

缺点：

需要训练，计算量大，原理相对复杂

需要建立适当的模型，需要充足的训练样本

　　总之异常检测的通用方法大致有４种：基于模型、k近邻、基于密度和基于聚类的。实际使用数据是线上的报价，由于每个SPU下报价有限，聚类不适合，所以用基于模型的和k近邻的做了试验；基于密度的和K近邻差不多，而且需要密度范围的距离阈值，就没有选择。此外，涉及的实验数据是公司的，代码是兴趣使然，所以就不公布具体实验数据。

　　路漫漫其修远兮，很多时候感觉想法比较幼稚。首先东西比较简单，其次工作也比较忙，还好周末可以抽时间处理这个。由于相关知识积累有限，欢迎大家提意见斧正，在此表示感谢！后续版本会持续更新…