求一个数组的数字有几种组合方式，6个数相加等于100.用PHP写的程式

Posted 2023-05-17

参考技术A

求一个数组的数字有几种组合方式，6个数相加等于100.用php写的程式

例如,已知有1,2,5,11,20这五个数字,要挑选出和为16的那几个数字,运用函式后,即挑出5和11 做法如下,你按照公式套进去就好: A1:A5分别...按住CTRL键 选择要抽出的数字 和在EXCEL下方显示 望采纳,谢谢

0到6的任意5个数相加等于11，可重复，有几种组合

有25种

可以把0当成补位的数，那么最少的数相加等于11就是5+6=11（其余3个数用0）

然后将5、6不断拆分成其他组合

0 0 0 5 6

0 0 1 4 6

0 0 1 5 5

0 0 2 3 6

0 0 2 4 5

0 0 3 3 5

0 0 3 4 4

0 1 1 3 6

0 1 1 4 5

0 1 2 2 6

0 1 2 3 5

0 1 2 4 4

0 1 3 3 4

0 2 2 2 5

0 2 2 3 4

0 2 3 3 3

1 1 1 2 6

1 1 1 3 5

1 1 1 4 4

1 1 2 2 5

1 1 2 3 4

1 1 3 3 3

1 2 2 2 4

1 2 2 3 3

2 2 2 2 3

从1到35,选6个数相加总和等于108有几种组合

经过程式设计计算，一共有27594种组合：
1+2+3+33+34+35=108
…………………………
15+16+17+19+20+21=108

7个数字有几种组合方法?

每位数可重复的话 9*10*10*10*10*10*10=9000000
不可重复9*9*8*7*6*5*4=544320

1-33的数中，6个数相加等于97的，有几种演算法

经过程式设计计算，共有19599种演算法：
1+2+3+26+32+33=97
……………………
13+14+16+17+18+19=97

数字1，2，3，4，5有几种组合方式

5×4×3×2×1=120种
希望能帮到您，我用的是手机，如果有疑问请发讯息问我，我收不到追问~O(∩_∩)O

5个数字相加（可重复）等于23的组合有几种

解析：
9+9+3+1+1=23
9+9+2+2+1=23
9+8+3+1+2=23
9+8+2+2+2=23

1到35的数,任意5个数相加等于99,有几种演算法

前提：不相同的五个数共有5466个
99=1+2+27+34+35; 99=1+2+28+33+35; 99=1+2+29+32+35; 99=1+2+29+33+34; 99=1+2+30+31+35; 99=1+2+30+32+34; 99=1+2+31+32+33; 99=1+3+26+34+35; 99=1+3+27+33+35; 99=1+3+28+32+35; 99=1+3+28+33+34; 99=1+3+29+31+35; 99=1+3+29+32+34; 99=1+3+30+31+34; 99=1+3+30+32+33; 99=1+4+25+34+35; 99=1+4+26+33+35; 99=1+4+27+32+35; 99=1+4+27+33+34; 99=1+4+28+31+35; 99=1+4+28+32+34; 99=1+4+29+30+35; 99=1+4+29+31+34; 99=1+4+29+32+33; 99=1+4+30+31+33; 99=1+5+24+34+35; 99=1+5+25+33+35; 99=1+5+26+32+35; 99=1+5+26+33+34; 99=1+5+27+31+35; 99=1+5+27+32+34; 99=1+5+28+30+35; 99=1+5+28+31+34; 99=1+5+28+32+33; 99=1+5+29+30+34; 99=1+5+29+31+33; 99=1+5+30+31+32; 99=1+6+23+34+35; 99=1+6+24+33+35; 99=1+6+25+32+35; 99=1+6+25+33+34; 99=1+6+26+31+35; 99=1+6+26+32+34; 99=1+6+27+30+35; 99=1+6+27+31+34; 99=1+6+27+32+33; 99=1+6+28+29+35; 99=1+6+28+30+34; 99=1+6+28+31+33; 99=1+6+29+30+33; 99=1+6+29+31+32; 99=1+7+22+34+35; 99=1+7+23+33+35; 99=1+7+24+32+35; 99=1+7+24+33+34; 99=1+7+25+31+35; 99=1+7+25+32+34; 99=1+7+26+30+35; 99=1+7+26+31+34; 99=1+7+26+32+33; 99=1+7+27+29+35; 99=1+7+27+30+34; 99=1+7+27+31+33; 99=1+7+28+29+34; 99=1+7+28+30+33; 99=1+7+28+31+32; 99=1+7+29+30+32; 99=1+8+21+34+35; 99=1+8+22+33+35; 99=1+8+23+32+35; 99=1+8+23+33+34; 99=1+8+24+31+35; 99=1+8+24+32+34; 99=1+8+25+30+35; 99=1+8+25+31+34; 99=1+8+25+32+33; 99=1+8+26+29+35; 99=1+8+26+30+34; 99=1+8+26+31+33; 99=1+8+27+28+35; 99=1+8+27+29+34; 99=1+8+27+30+33; 99=1+8+27+31+32; 99=1+8+28+29+33; 99=1+8+28+30+32; 99=1+8+29+30+31; 99=1+9+20+34+35; 99=1+9+21+33+35; 99=1+9+22+32+35; 99=1+9+22+33+34; 99=1+9+23+31+35; 99=1+9+23+32+34; 99=1+9+24+30+35; 99=1+9+24+31+34; 99=1+9+24+32+33; 99=1+9+25+29+35; 99=1+9+25+30+34; 99=1+9+25+31+33; 99=1+9+26+28+35; 99=1+9+26+29+34; 99=1+9+26+30+33; 99=1+9+26+31+32; 99=1+9+27+28+34; 99=1+9+27+29+33; 99=1+9+27+30+32; 99=1+9+28+29+32; 99=1+9+28+30+31; 99=1+10+19+34+35; 99=1+10+20+33+35; 99=1+10+21+32+35; 99=1+10+21+33+34; 99=1+10+22+31+35; 99=1+10+22+32+34; 99=1+10+23+30+35; 99=1+10+23+31+34; 99=1+10+23+32+33; 99=1+10+24+29+35; 99=1+10+24+30+34; 99=1+10+24+31+33; 99=1+10+25+28+35; 99=1+10+25+29+34; 99=1+10+25+30+33; 99=1+10+25+31+32; 99=1+10+26+27+35; 99=1+10+26+28+34; 99=1+10+26+29+33; 99=1+10+26+30+32; 99=1+10+27+28+33; 99=1+10+27+29+32; 99=1+10+27+30+31; 99=1+10+28+29+31; 99=1+11+18+34+35; 99=1+11+19+33+35; 99=1+11+20+32+35; 99=1+11+20+33+34; 99=1+11+21+31+35; 99=1+11+21+32+34; 99=1+11+22+30+35; 99=1+11+22+31+34; 99=1+11+22+32+33; 99=1+11+23+29+35; 99=1+11+23+30+34; 99=1+11+23+31+33; 99=1+11+24+28+35; 99=1+11+24+29+34; 99=1+11+24+30+33; 99=1+11+24+31+32; 99=1+11+25+27+35; 99=1+11+25+28+34; 99=1+11+25+29+33; 99=1+11+25+30+32; 99=1+11+26+27+34; 99=1+11+26+28+33; 99=1+11+26+29+32; 99=1+11+26+30+31; 99=1+11+27+28+32; 99=1+11+27+29+31; 99=1+11+28+29+30; 99=1+12+17+34+35; 99=1+12+18+33+35; 99=1+12+19+32+35; 99=1+12+19+33+34; 99=1+12+20+31+35; 99=1+12+20+32+34; 99=1+12+21+30+35; 99=1+12+21+31+34; 99=1+12+21+32+33; 99=1+12+22+29+35; 99=1+12+22+30+34; 99=1+12+22+31+33; 99=1+12+23+28+35; 99=1+12+23+29+34; 99=1+12+23+30+33; 99=1+12+23+31+32; 99=1+12+24+27+35; 99=1+12+24+28+34; 99=1+12+24+29+33; 99=1+12+24+30+32; 99=1+12+25+26+35; 99=1+12+25+27+34; 99=1+12+25+28+33; 99=1+12+25+29+32; 99=1+12+25+30+31; 99=1+12+26+27+33; 99=1+12+26+28+32; 99=1+12+26+29+31; 99=1+12+27+28+31; 99=1+12+27+29+30; 99=1+13+16+34+35; 99=1+13+17+33+35; 99=1+13+18+32+35; 99=1+13+18+33+34; 99=1+13+19+31+35; 99=1+13+19+32+34; 99=1+13+20+30+35; 99=1+13+20+31+34; 99=1+13+20+32+33; 99=1+13+21+29+35; 99=1+13+21+30+34; 99=1+13+21+31+33; 99=1+13+22+28+35; 99=1+13+22+29+34; 99=1+13+22+30+33; 99=1+13+22+31+32; 99=1+13+23+27+35; 99=1+13+23+28+34; 99=1+13+23+29+33; 99=1+13+23+30+32; 99=1+13+24+26+35; 99=1+13+24+27+34; 99=1+13+24+28+33; 99=1+13+24+29+32; 99=1+13+24+30+31; 99=1+13+25+26+34; 99=1+13+25+27+33; 99=1+13+25+28+32; 99=1+13+25+29+31; 99=1+13+26+27+32; 99=1+13+26+28+31; 99=1+13+26+29+30; 99=1+13+27+28+30; 99=1+14+15+34+35; 99=1+14+16+33+35; 99=1+14+17+32+35; 99=1+14+17+33+34; 99=1+14+18+31+35; 99=1+14+18+32+34; 99=1+14+19+30+35; 99=1+14+19+31+34; 99=1+14+19+32+33; 99=1+14+20+29+35; 99=1+14+20+30+34; 99=1+14+20+31+33; 99=1+14+21+28+35; 99=1+14+21+29+34; 99=1+14+21+30+33; 99=1+14+21+31+32; 99=1+14+22+27+35; 99=1+14+22+28+34; 99=1+14+22+29+33; 99=1+14+22+30+32; 99=1+14+23+26+35; 99=1+14+23+27+34; 99=1+14+23+28+33; 99=1+14+23+29+32; 99=1+14+23+30+31; 99=1+14+24+25+35; 99=1+14+24+26+34; 99=1+14+24+27+33; 99=1+14+24+28+32; 99=1+14+24+29+31; 99=1+14+25+26+33; 99=1+14+25+27+32; 99=1+14+25+28+31; 99=1+14+25+29+30; 99=1+14+26+27+31; 99=1+14+26+28+30; 99=1+14+27+28+29; 99=1+15+16+32+35; 99=1+15+16+33+34; 99=1+15+17+31+35; 99=1+15+17+32+34; 99=1+15+18+30+35; 99=1+15+18+31+34; 99=1+15+18+32+33; 99=1+15+19+29+35; 99=1+15+19+30+34; 99=1+15+19+31+33; 99=1+15+20+28+35; 99=1+15+20+29+34; 99=1+15+20+30+33; 99=1+15+20+31+32; 99=1+15+21+27+35; 99=1+15+21+28+34; 99=1+15+21+29+33; 99=1+15+21+30+32; 99=1+15+22+26+35; 99=1+15+22+27+34; 99=1+15+22+28+33; 99=1+15+22+29+32; 99=1+15+22+30+31; 99=1+15+23+25+35;
…………
加上vb程式码
Dim a%, b%, c%, d%, e%, s%, F(1 To 6000) As String, i&
F(1) = "": i = 1
For a = 1 To 35
For b = a + 1 To 35
For c = b + 1 To 35
For d = c + 1 To 35
For e = d + 1 To 35
s = a + b + c + d + e
If s = 99 Then
i = i + 1
F(i) = F(i - 1) + Trim(s & "=" & a & "+" & _
b & "+" & c & "+" & d & "+" & e) + "; "
End If
Next e
Next d
Next c
Next b
Next a
Text1.Text = "前提：不相同的五个数共有" & i - 1 & "个" & F(i)

有关PHP阵列的问题,3个数组合成一个数组的阵列.

$a1=array("a","b","c","d");
$a2=array("2","3","4","5");
$a3=array("a1","a3","a4","a4");
$a4=array();
foreach($a1 as $key=>$item)
$a4[$key][]=$item;
$a4[$key][]=$a2[$key];
$a4[$key][]=$a3[$key];

print_r($a4);

4个数相加等于10的有几组

1十2十3十5=10，1十2十4十3=10，
答:4个数相加等于10的只有两组，再组会数字重
复。

求最大子数组（循环数组）

一.设计思想：

　　通过一个for循环。数组分别从0-最大，1-最大-0 等等依次 到最大-最大-1，通过这样的方式达到循环数组的目的。然后在每一个的数字里面，从第一个数开始向后按顺序相加，当相加结果为负数的时候，则此时不满足构成最大子数组的条件，然后从导致数组为负数的数的下一个数开始向后相加。最后求得此情况下的最大子数组和。然后分别求出N个最大子数组的和，然后在进行比较大小，得出最终的最大子数组的和。

二.出现的问题：

　　起初并没有实现在一个首尾相接的数组中，最大子数组和为正确值，例如 1 -2 -3 6 5 正确结果为12 最后得出结果为11。

三.问题的解决

　  通过大for循环里面嵌套小循环，来实现的数组的循环问题。然后在每个小循环里面求出最大的子数组和。最后再比较大小来求出最大子数组的和。

四.源代码：

package maxs;
import java.util.*;
public class maxs {
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in); 
        int num;
        System.out.println("请输入数组长度");
        num=sc.nextInt();
        int zif[]=new int[num];//分别的数组
        int neir[]=new int[num]; //数组里面的数
        int sum1[]=new int[num]; //最大值
        int d=sum1[0];
        System.out.println("请输入数组内容：");
        for(int i=0;i<num;i++)//输入num个数
        {
            neir[i]=sc.nextInt();
        }       
         for(int j=0;j<num;j++)   
        {
            for(int k=0;k<num;k++)   //分别从0-num 1-num-0 .....
            {
                zif[k]=neir[(j+k)%num];
            }
            int sum=zif[0];//记录数组和
            int b=0;//进行记录
        
            for(int i=0;i<num;i++)
            {
                if(b<0)
                {
                    b=zif[i]; //b<0,b为加为负数那位的后一位
                }
                else
                {
                    b+=zif[i];
                }
                if(sum<b)
                {
                    sum=b; //sum为当前最大子数组的和
                }
                sum1[j]=sum;
            }
            if(d<sum1[j])
            {
                d=sum1[j]; //得到最终的最大和
            }
        }
        System.out.print("最大子数组和为：");
        System.out.print(d);
    }
}

 

五.结果截图：

　　

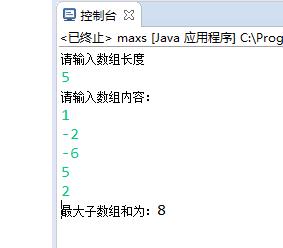
六.总结：

　　一个首尾相接的循环数组，可以在不同的位置起始。一个循环的数组可以分为从不同的位置开始。然后从第一个数，到最后一个数，每个数都当一次开始然后依次下去到结束。这样的N个数组凑起来就是一个首尾相接的循环数组。子数组的最大和则可以让开始的数开始向后面相加，当遇到结果为负数的时候，就不在满足条件了。应该从加的最后一个数的下一个数再开始进行相加。

　　我的收获的就是：起初自己并没有思路，不知道怎么来实现他。然后想想老师说的剪断，那么不就是分别在第一个数后， 第二个数后，，，依次来当作断点吗？将复杂问题，分解，让问题明白了许多。