最后的挣扎--蓝桥杯Java2021B组题解
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最后的挣扎--蓝桥杯Java2021B组题解相关的知识,希望对你有一定的参考价值。
文章目录
前言
昨天随便瞄了一眼去年的Java B组的题目,一来就先搞出4题,当然不保证是最优解。
今天主要还是以阐述思路为主,适当优化别人的代码,毕竟这种题解网上都不少,我只是再把具体的思路复述一遍,力求能够摸清楚一点套路。
我们按照题目难度来说名。
首先是昨天的4题,不用想,这个妥妥送分。
ASC

public class ASC
public static void main(String[] args)
System.out.println((int) 'L');
卡片

public class 卡片
//由题意知道1的消耗是最大的,所以没有必要去把0-9的那个去统计
static int count = 2021;
public static void main(String[] args)
for (int i = 1; i <=10000; i++)
String temp = String.valueOf(i);
if(temp.contains("1"))
for (char c : temp.toCharArray())
if(c=='1')
count--;
if(count==0)
System.out.println(temp);
break;
else if (count<0)
System.out.println(i-1);
break;
时间限制
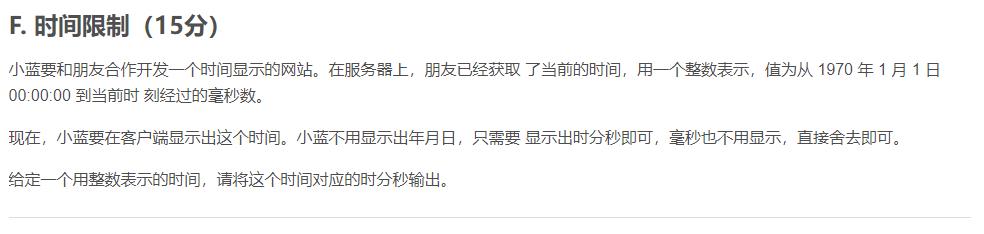
class Time
public static void main(String[] args)
Scanner scanner = new Scanner(System.in);
long time = scanner.nextLong();
time /=1000;
int a= (int) (time % (24 * 3600));
int h = a / 3600;
a %= 3600;
int m = a/60;
int s = a%60;
System.out.printf("%02d:%02d:%02d\\n",h,m,s);
这里值得一提的是 java 其实还提供了printf()这个函数,所以我们不需要输出的那么辛苦。
杨辉三角

昨天太晚了,没注意,给的代码是原来没调好的。
public class 杨辉三角
static int[] yanghui;//搞大一点
public static void main(String[] args)
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
if(n==1)
System.out.println(n);
yanghui = new int[1000000];//搞一点,理论上可以先算一个阈值 n*n/2 <=10000000
yanghui[0]=1;
yanghui[1]=1;
yanghui[2]=1;
int idx = 2; //当前第第几个
for (int i=3;;i++)
//卡阈值死磕,来骗~,现在是从第三层开始
idx++;
yanghui[idx]=1;
int j=1;
for (;j<i-1;j++)
idx++;
yanghui[idx]=yanghui[idx-(i)]+yanghui[idx+1-i];
//条件判断
if(yanghui[idx]==n)
System.out.println(idx+1);
return;
idx++;
yanghui[idx]=1;
怎么说呢,肯定不是最优解,不过骗到是应该能够骗点分数。
货物摆放

说句实话,我对这种题目不是很敏感,意思其实很好理解,说白了就是 一个数组,你去组合成三个数字,然后相乘等于自己本身。
我当时的第一想法肯定是暴力,暴力枚举 但是 n的三次幂挺大的。所以我就在想这些数有没有什么规律啥的。然后,什么数字相乘能够得到自己本身,那么不就是可以被自己整除的数子嘛,也就是约数呀。所以代码出来了。
求取约数
首先我们要做的是求约数,这里的话是有一个公式的。
首先是最简单的
for(int i=1;i<=Math.sqrt(n);i++)
if(n%i==0)
res.add(i);
res.add(n/i);
这个的时间复杂度是O log n
本来是这样的,但是由于你的 i 都是小于人家方根的,所以后面那个if一定成立,减少了很多不必要的运算。
for(int i=1;i<Math.sqrt(n);i++)
if(n%i==0)
res.add(i);
if(i*i!=n)
res.add(n/i);
public class 货物摆放
static int ans = 0;
static long num = 2021041820210418L;
public static void main(String[] args)
long end = (long)Math.sqrt(num);
Set<Long> div = new HashSet<>();
for (long i = 1; i <= end; i++)
if (num % i == 0)
div.add(num/i);
div.add(i);
Long[] arr = div.toArray(new Long[0]);
for (long i : arr)
for (long j : arr)
for (long k : arr)
if (i * j * k == num)
ans++;
System.out.println(ans);
直线

这两个填空题的话,怎么说呢,难度上其实都应该差不多,不过这个直线的创新性稍微强一点。
这里的想法也很简单,没错就是生成那个矩阵,然后去枚举,重点是去重,这里去重的话,直接考虑使用Set。反正都是暴力。
我们这边就先考虑 有斜线的情况,不考虑连接成与坐标轴平行的线。
后面再加回去嘛,主要是公式这边不好处理。
public class 直线
public static void main(String[] args)
Set<Map<Double,Double>> linear = new HashSet<>();
List<Map<Integer,Integer>> points = new ArrayList<>();
//初始化所有点
for (int i=0;i<20;i++)
for(int j=0;j<21;j++)
HashMap<Integer, Integer> temp = new HashMap<>();
temp.put(i,j);
points.add(temp);
//遍历计算点
for (int i=0;i<points.size();i++)
for(int j=i+1;j<points.size();j++)
double x1=0;double y1=0;
double x2=0;double y2=0;
//解包
for (Map.Entry<Integer, Integer> point1 : points.get(i).entrySet())
x1=point1.getKey();
y1=point1.getValue();
for (Map.Entry<Integer, Integer> point1 : points.get(j).entrySet())
x2=point1.getKey();
y2=point1.getValue();
if(x1==x2||y1==y2)
continue;
//水平的情况,先不要
//计算斜率
double k=(y2-y1)/(x2-x1);
double b=(x2*y1 -x1*y2)/(x2-x1);
HashMap<Double, Double> temp = new HashMap<>();
temp.put(k,b);
//对于这种数据类型,equal方法是按照值去对比的
linear.add(temp);
System.out.println(linear.size()+20+21);
路径
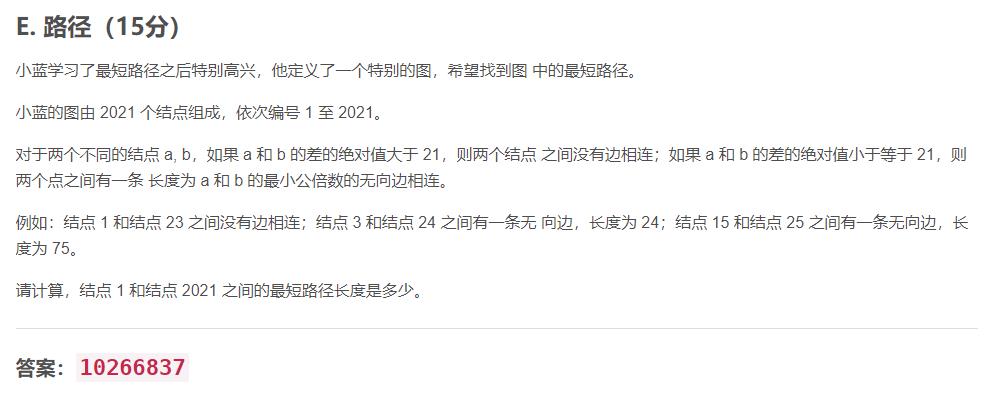
这个题目本身不是很难,主要是构建那个图稍微麻烦一点。
构建好之后,咱们再去找最短路径。
这里有两个算法一个是 弗洛伊德,还有一个是 迪杰特斯 的方法。
最简单的当然是第一个。
public class Main
static int[][] graph = new int[2050][2050];
static final int INF = 0x3f3f3f3f;
private static void floyd()
for (int k = 1; k <= 2021; k++)
for (int i = 1; i <= 2021; i++)
for (int j = 1; j <= 2021; j++)
if (i != j && graph[i][j] > graph[i][k] + graph[k][j])
graph[i][j] = graph[i][k] + graph[k][j];
private static int gcd(int a, int b)
return b == 0 ? a : gcd(b, a % b);
public static void main(String[] args)
for (int i = 1; i <= 2021; i++)
for (int j = 1; j <= 2021; j++)
graph[i][j] = INF;
for (int i = 1; i <= 2021; i++)
int st = Math.max(i - 21, 1);
for (int j = st; j <= i; j++)
int div = gcd(j, i);
int lcm = i * j / div;
graph[i][j] = lcm;
graph[j][i] = lcm;
floyd();
System.out.println(graph[1][2021]); // 10266837
这里简单说一下原理。其实很简单

看那个大循环就知道了,A–》B假设走A中转看距离,然后走完后,在假设走B中转,知道假设玩全部。
例如A–》D 第2次遍历假设到走B近,那么此时更新到B中转,然后再问遍历的C中转,发现在原来的基础上还更近,那么此时再加上走C的距离,此时你就得到了A–》D 中转 B C 近。
接的下来是后面三道大题冲刺。 按照刷题的经验,基本上第十题应该是最难的,第一题应该是简单的,其他的不好说,所以一定要先全部预览一下题目。包括,昨天,我就是9,10题基本上没看,以为很难。结果第九题嘿嘿,还是能骗分的。
到这里,已经“大力飞砖”了大概 7 题,其实发现,这些题目,比原来的数据量大,填空题几乎不可能手推出来,而且考到了比较多的数据结构方面的东西,对比原来的 13 14 包括20 和原来的模拟题怎么说呢,题目是越来越绕了。我这糟糕的语文能力。
双向队列

这里还要我说嘛,工具类,暴力来骗~
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Main
public static void main(String[] args)
Scanner in = new Scanner(new BufferedInputStream(System.in));
int n = in.nextInt(), m = in.nextInt();
Integer[] arr = new Integer[n + 1];
for (int i = 1; i <= n; i++)
arr[i] = i;
for (int i = 0; i < m; i++)
int p = in.nextInt();
int split = in.nextInt();
if (p == 0)
Arrays.sort(arr, 1, split + 1, (a, b) -> Integer.compare(b, a));
else
Arrays.sort(arr, split, n + 1);
for (int i = 1; i <= n; i++)
if (i > 1)
System.out.print(" ");
System.out.print(arr[i]);
in.close();
这里有一个输入优化,请务必记住
new Scanner(new BufferedInputStream(System.in))
到此,好骗的大题目估计就骗到了~
括号匹配
为什么先说在这个咧,原因很简单,dp,我想不出来,我只能想到暴力!
public class 括号匹配
static int count 以上是关于最后的挣扎--蓝桥杯Java2021B组题解的主要内容,如果未能解决你的问题,请参考以下文章