灰色预测改进—三角残差拟合_python

Posted 2022-04-08 hellobigorange

😊四月的第一篇博客，希望一整个四月都可以开开心心、顺顺利利呀。好运发射给读到这篇博客的每个人。biu,biu,biu~~~

02/04/2022 16:00

---

灰色系统理论及其应用系列博文：
一、灰色关联度分析法(GRA)_python
二、灰色预测模型GM(1,1)
三、灰色预测模型GM(1,n)
四、灰色预测算法改进1_背景值Z的改进
五、灰色预测改进2—三角残差拟合

---

注：本文所有的算法及理论均来自论文A trigonometric grey prediction approach to forecasting electricity demand.

---

文章目录

• • 一、基于三角残差拟合的算法
  • • 1、算法
    • 2、扩展到区间预测
    • 3、实例
    • • 3.1 代码
      • 3.2 结果

参考文献：

[1] A trigonometric grey prediction approach to forecasting electricity demand.

---

一、基于三角残差拟合的算法

该算法适用于拟合既有线性趋势又有周期趋势（季节性）且数据量较少的序列。

1、算法

• 获取残差序列
  

• 三角函数模型处理残差序列
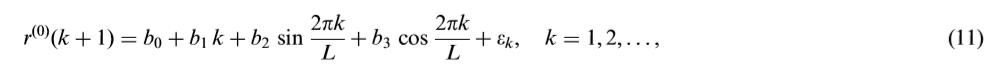
  L是用户自定义循环周期分量，$\epsilon$是随机分量。对于季度的电力需求，有L=4；对于月度的电力需求，有L=12。注意因为季节效应显然是主要的循环变化。 对于年用电量，L 应该反映经济波动的周期性周期，取决于历史数据量。当有大约 20 年的年度数据时，我们的建议是 $15\le L\le 30$，因为根据我们的初步实验，这样的选择可能很好地捕捉到残差序列的模式。同时，由最小二乘法可以得到：
  

• 获得残差序列的预测值${\hat{r}}^{(0)}(k)$
  

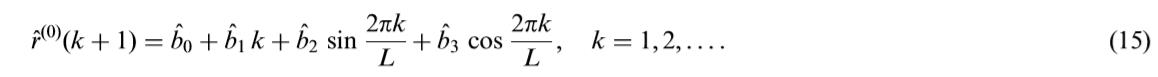
• 获得灰度预测值
  
  其中${\hat{x}}_{tr}^{(0)}(k)$表示GM(1,1)模型的输出${\hat{x}}^{(0)}(k)$的预测值。

2、扩展到区间预测

上述讨论都是基于点的预测， 为了平衡电力公司运营和管理中的供需，合理的电力需求区间预测是非常有用的。文献 [1] 提供了年电力需求的灰色预测区间，但他们的方法仅限于原始 GM(1,1) 模型。 我们现在将为我们的三角灰色预测模型提供一个预测区间。

请注意，方程给出的三角残差修正模型。 (11) 本质上是一个多元线性回归模型。 由于GM(1,1) 模型和三角残差修正模型分别有两个和四个参数，我们的三角灰色预测方法占据的总自由度是六个。 当历史数据点数超过6个时，可以用过大的自由度来估计残差的方差，然后再估计预测区间。 相反，在傅里叶灰色预测方法中，几乎所有的自由度都用于参数估计。

遵循多元回归分析中区间预测的思想，我们给出了${\hat{x}}^{(0)}(k)$ 的 $100(1-\alpha )$% 预测区间如下：

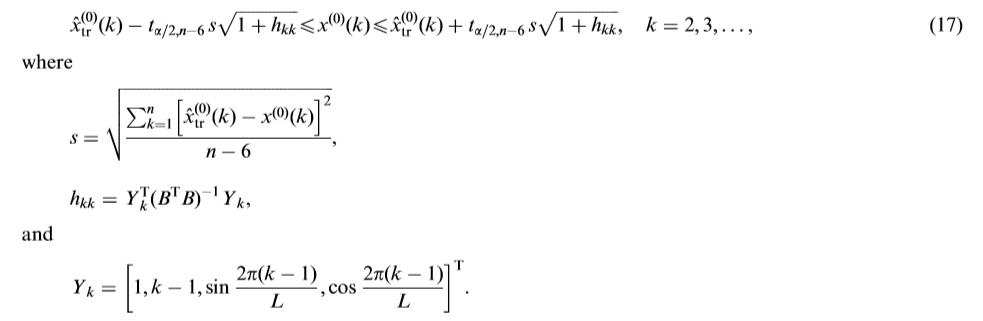
3、实例

我们首先对中国年度电力需求预测进行实证说明，以检验我们的三角灰色预测方法的性能。由于 1970 年代后期改革开放前后经济发展方式的不同，这两个时期中国的用电模式也大相径庭。因此，我们在研究中使用了 1980 年以后的年度电力需求数据。数据来自中国统计年鉴，其中1981-1998年的数据用于模型构建，而1999-2002年的数据用作事后测试数据集。

当使用三角灰色预测方法对中国年电力需求进行建模和预测时，我们使用 $L=23$，因为这是推荐界限的平均值。 我们的初步实验表明，在本案例研究的推荐区间内，预测值对 L 非常不敏感。
但是，这并不意味着原始 GM(1,1) 预测的残差没有周期性变化。 从Fig.1中我们可以发现，残差呈现出一些周期性变化，并且幅度随着时间的推移变得越来越大。 在此图中，预测值对 L 不敏感的一个可能原因是年度数据案例的残差的季节性可能不强。

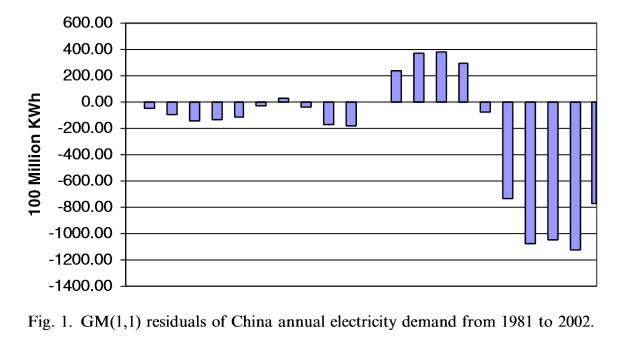
下面将采用原始的GM(1,1)算法，和基于三角残差拟合的GM(1,1)算法，给出两者的算法及效果对比：

3.1 代码

注意该代码中标有两个类，GM_trig和GM11，其中，GM11是原始的灰度预测算法类；GM_trig是三角残差拟合的算法类。

# -*- coding: utf-8 -*-
# @Time : 2022/3/30 14:44
# @Author : Orange
# @File : gm_trigonometric.py


from decimal import *
import math


class GM_trig():
    def __init__(self, X0, X0_hat, L):
        '''
        :param X0: 原始序列
        :param X0_hat: 采用GM(1,1)后获得的序列
        :param L: 用户自定义的循环周期分量
        '''
        self.X0 = X0
        self.X0_hat = X0_hat
        self.R0 = (X0 - X0_hat)[1:]  # 残差
        self.L = L
        self.n = len(self.X0)
        self.B = None

    def train(self):
        self.B = np.array(
            [[1] * (self.n - 1), np.arange(1, self.n), [np.sin(2 * i * math.pi / self.L) for i in range(1, self.n)],
             [np.cos(2 * i * math.pi / self.L) for i in range(1, self.n)]]).T
        R_n = np.array(self.R0).reshape(self.n - 1, 1)
        b_hat = np.linalg.inv(np.matmul(self.B.T, self.B)).dot(self.B.T).dot(R_n)
        self.f_R0 = lambda k: b_hat[0][0] + b_hat[1][0] * k + b_hat[2][0] * np.sin(2 * k * math.pi / self.L) + b_hat[3][
            0] * np.cos(2 * k * math.pi / self.L)

    def predict(self, k, X_all_0_hat):
        '''

        :param k: 给出从0，k的预测值
        :param X_all_0_hat: 所有数据（训练+测试）的GM(1,1)预测值列表
        :return:
        '''
        R0_hat = [self.f_R0(k) for k in range(1, k)]
        R0_hat.insert(0, 0)
        X_tr_hat = X_all_0_hat + R0_hat
        return X_tr_hat

    def interval_pred(self, X_tr_hat, t_val, k):
        s = math.sqrt(sum((X_tr_hat[:self.n] - self.X0) ** 2) / (self.n - 6))
        l_bound = []
        h_bound = []
        for k in range(1, k):
            Y_k = np.array([1, k, np.sin(2 * k * math.pi / self.L), np.cos(2 * k * math.pi / self.L)]).reshape(4, 1)
            h_kk = Y_k.T.dot(np.linalg.inv(np.matmul(self.B.T, self.B))).dot(Y_k)[0][0]
            ll_k = X_tr_hat[k] - t_val * s * math.sqrt(1 + h_kk)
            hh_k = X_tr_hat[k] + t_val * s * math.sqrt(1 + h_kk)
            l_bound.append(ll_k)
            h_bound.append(hh_k)
        return l_bound, h_bound


class GM11():
    def __init__(self):
        self.f = None

    def isUsable(self, X0):
        '''判断是否通过光滑检验'''
        X1 = X0.cumsum()
        rho = [X0[i] / X1[i - 1] for i in range(1, len(X0))]
        rho_ratio = [rho[i + 1] / rho[i] for i in range(len(rho) - 1)]
        print("rho:", rho)
        print("rho_ratio:", rho_ratio)
        flag = True
        for i in range(2, len(rho) - 1):
            if rho[i] > 0.5 or rho[i + 1] / rho[i] >= 1:
                flag = False
        if rho[-1] > 0.5:
            flag = False
        if flag:
            print("数据通过光滑校验")
        else:
            print("该数据未通过光滑校验")

        '''判断是否通过级比检验'''
        lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
        X_min = np.e ** (-2 / (len(X0) + 1))
        X_max = np.e ** (2 / (len(X0) + 1))
        for lambd in lambds:
            if lambd < X_min or lambd > X_max:
                print('该数据未通过级比检验')
                return
        print('该数据通过级比检验')

    def train(self, X0):
        X1 = X0.cumsum()
        Z = (np.array([-0.5 * (X1[k - 1] + X1[k]) for k in range(1, len(X1))])).reshape(len(X1) - 1, 1)
        # 数据矩阵A、B
        A = (X0[1:]).reshape(len(Z), 1)
        B = np.hstack((Z, np.ones(len(Z)).reshape(len(Z), 1)))
        # 求灰参数
        a, u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
        u = Decimal(u[0])
        a = Decimal(a[0])
        print("灰参数a：", a, "，灰参数u：", u)
        self.f = lambda k: (Decimal(X0[0]) - u / a) * np.exp(-a * k) + u / a

    def predict(self, k):
        X1_hat = [float(self.f(k)) for k in range(k)]
        X0_hat = np.diff(X1_hat)
        X0_hat = np.hstack((X1_hat[0], X0_hat))
        return X0_hat

    def evaluate(self, X0_hat, X0):
        '''
        根据后验差比及小误差概率判断预测结果
        :param X0_hat: 预测结果
        :return:
        '''
        S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
        S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
        C = S2 / S1  # 后验差比
        Pe = np.mean(X0 - X0_hat)
        temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1
        p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
        print("原数据样本标准差：", S1)
        print("残差样本标准差：", S2)
        print("后验差比：", C)
        print("小误差概率p：", p)


def MAPE(y_true, y_pred):
    """计算MAPE"""
    n = len(y_true)
    mape = sum(np.abs((y_true - y_pred) / y_true)) / n * 100
    return mape


if __name__ == '__main__':
    import matplotlib.pyplot as plt
    import numpy as np
    import pandas as pd

    plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
    plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）

    # 原始数据X
    data = pd.read_csv("test.csv")
    X = data["val"].values
    # 训练集
    X_train = X[:-4]
    # 测试集
    X_test = X[-4:]

    model = GM11()
    model.isUsable(X_train)  # 判断模型可行性
    model.train(X_train)  # 训练
    Y_pred = model.predict(len(X))  # 预测
    Y_train_pred = Y_pred[:len(X_train)]
    Y_test_pred = Y_pred[len(X_train):]
    score_test = model.evaluate(Y_test_pred, X_test)  # 评估
    print("gm(1,1)_mape:", MAPE(Y_train_pred, X_train), "%")

    model_trig = GM_trig(X_train, Y_train_pred, L=23)
    model_trig.train()
    result = model_trig.predict(len(X), Y_pred)
    X_train_pred = result[:-4]
    X_test_pred = result[-4:]
    l_bound, h_bound = model_trig.interval_pred(result, 2.179, len(X))

    # 可视化
    plt.grid()
    plt.plot(np.arange(len(X_train)), X_train, '->')
    plt.plot(np.arange(len(X_train)), X_train_pred, '-o')
    plt.plot(np.arange(len(X_train)), Y_train_pred, '-*')
    plt.legend(['负荷实际值', '三角残差预测值', 'GM(1,1)预测值'])
    print("gm(1,1)_trig_mape:", MAPE(X_train_pred, X_train), "%")
    plt.title('训练集')
    plt.show()

    # 可视化
    plt.grid()
    plt.plot(np.arange(len(X_test)), X_test, '->')
    plt.plot(np.arange(len(X_test)), X_test_pred, '-o')
    plt.plot以上是关于灰色预测改进—三角残差拟合_python的主要内容，如果未能解决你的问题，请参考以下文章
 
 Python：使用灰色预测对数据进行预测
 Python：使用灰色预测对数据进行预测
 灰色预测GM(1,n)模型_python
 R语言plotly可视化：使用plotly可视化简单线性回归模型的回归线对比不同参数设置下的同一机器学习模型算法的拟合曲线三维回归曲面可视化实际值和回归预测值的散点图残差分析
 R语言lm函数拟合多元线性回归模型（无交互作用）并诊断模型diagnostics使用plot函数打印回归模型的Q-Q图残差拟合图标度-位置图残差与杠杆关系图
 Python使用matplotlib可视化时间序列数据的分解图将时间序列数据进行分解并可视化分解为趋势季节和残差等成分（Time Series Decomposition Plot）