概率论与数理统计猴博士 笔记 p1-p2 古典概型几何概型

Posted 2022-04-08 karshey

视频

古典概型

常见的古典概型题目分为：

1. 有放回
2. 无放回

有放回

对于有放回的题目，一般可以这样做：

举个例子，如题：

则它们的答案是：
1.
$$C_4^4\ast （\frac{2}{5}{）}^4$$
2.
$$C_4^2\ast （\frac{2}{5}{）}^2\ast C_2^2\ast （\frac{1}{5}{）}^2$$
3.
$$C_4^2\ast （\frac{2}{5}{）}^2\ast C_2^1\ast （\frac{1}{5}）\ast C_1^1\ast （\frac{1}{5}）$$

无放回

一般是：摸东西，但是不会只摸一个，问同时摸到某些东西的概率（无放回）。
一般做法：

如题：

则它们的答案是：
1.
$$（\frac{C_5^3}{C_{10}^3}）$$
2.
$$（\frac{C_5^2\ast C_3^1}{C_{10}^3}）$$
3.
$$（\frac{C_5^1\ast C_3^1\ast C_2^1}{C_3^{10}}）$$

一个小练习：

显然是无放回的。

答案：

$$（\frac{C_{100}^2\ast C_{300}^1}{C_{700}^3}）$$

几何概型

通过画图的方求概率的题型。常见的几何概型的题目如下：

1. 有范围
2. 给若干数
3. 求数在范围内的概率
   

做法：画图。
步骤：

例题1与答案：

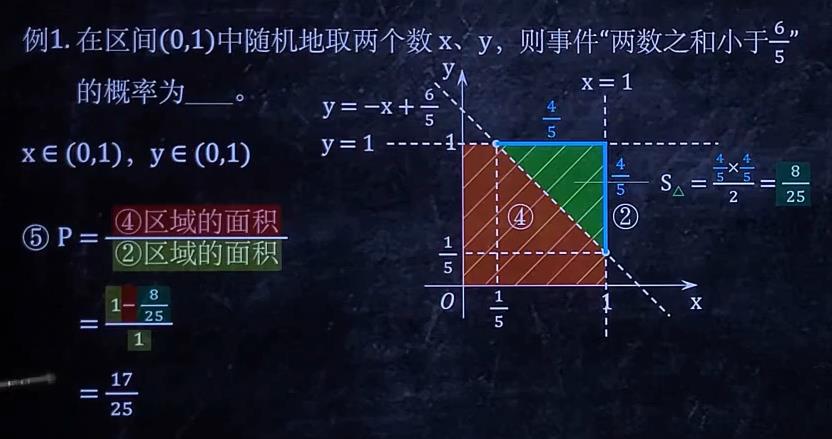
例题2：

答案：

例3与例4：

例3答案：

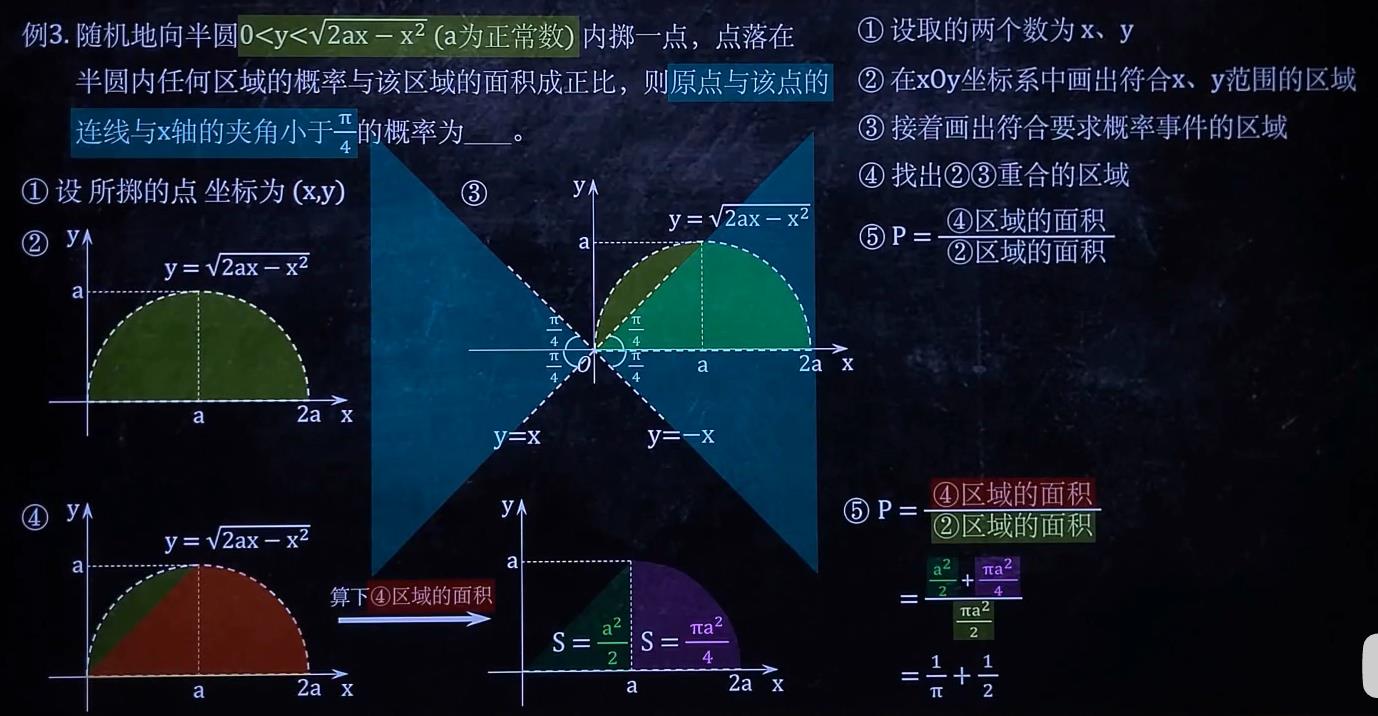
例4答案：