翻译: 3.7. Softmax 回归的简明实现 pytorch

Posted 2022-04-05 AI架构师易筋

正如深度学习框架的高级 API 使第 3.3 节中的线性回归实现变得更加容易一样，我们会发现它同样（或可能更方便）实现分类模型。让我们坚持使用 Fashion-MNIST 数据集，并将批量大小保持在 256，如第 3.6 节所示。

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

3.7.1. 初始化模型参数

如3.4 节所述，softmax 回归的输出层是一个全连接层。因此，要实现我们的模型，我们只需要在我们的Sequential. 同样，在这里，这Sequential并不是真正必要的，但我们不妨养成这种习惯，因为它在实现深度模型时无处不在。同样，我们以零均值和标准差 0.01 随机初始化权重。
图片大小为 28 x 28 = 784， 2维图片矩阵拉为一维784向量.

# PyTorch does not implicitly reshape the inputs. Thus we define the flatten
# layer to reshape the inputs before the linear layer in our network
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

3.7.2. 重新审视 Softmax 实现

在第 3.6 节的前面示例中，我们计算了模型的输出，然后通过交叉熵损失运行该输出。从数学上讲，这是一件完全合理的事情。然而，从计算的角度来看，求幂可能是数值稳定性问题的根源。

如果我们想通过我们的模型评估输出概率，我们将希望保留传统的 softmax 函数。但是，我们不会将 softmax 概率传递到我们的新损失函数中，而是只传递 logits 并在交叉熵损失函数中一次计算 softmax 及其对数，它会做一些聪明的事情，比如 “LogSumExp 技巧”。

loss = nn.CrossEntropyLoss(reduction='none')

3.7.3. 优化算法

在这里，我们使用学习率为 0.1 的小批量随机梯度下降作为优化算法。请注意，这与我们在线性回归示例中应用的相同，它说明了优化器的一般适用性。

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

3.7.4. 训练

接下来我们调用3.6节定义的训练函数 来训练模型。

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

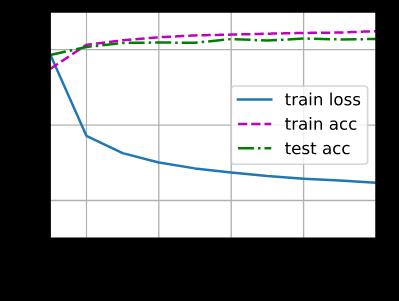
和以前一样，这个算法收敛到一个可以达到相当准确度的解决方案，尽管这次的代码行数比以前少。

3.7.5 概括

• 使用高级 API，我们可以更简洁地实现 softmax 回归。

• 从计算的角度来看，实现 softmax 回归具有复杂性。请注意，在许多情况下，深度学习框架会在这些最著名的技巧之外采取额外的预防措施来确保数值稳定性，从而避免我们在实践中尝试从头开始编写所有模型时遇到的更多陷阱。

3.7.6 练习

1. 尝试调整超参数，例如批量大小、时期数和学习率，看看结果如何。

2. 增加训练的 epoch 数。为什么一段时间后测试精度会下降？我们怎么能解决这个问题？

参考

https://d2l.ai/chapter_linear-networks/softmax-regression-concise.html