[硫化铂]舰队游戏

Posted 2022-04-04 StaroForgin

舰队游戏

题目概述

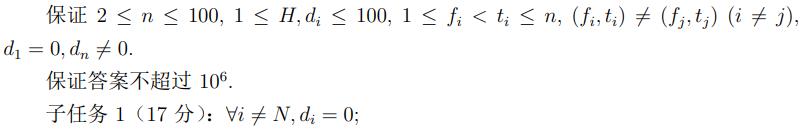
题解

首先，如果不涉及最后一个脱离海域的操作的话，我们就可以直接用拓扑解决，就是一个期望的dp。
但有了这一个操作，我们就可以在一些显然不可以达到最优解的情形下选择这个回退的操作，从起点开始再跑一遍。
这样我们的转移方程就会发生一定的变化，我们先记$d{p}_{i,j}$表示从点$i$出发，拥有$j$的生命力走到点$n$的期望花费时间。
我们最开始可以知道的一种一定会回退的点就是不能够走到我们真正终点，我们可以在只回退这种点的情况下跑一次拓扑，求出一个解。
但这个解可能是大于我们的答案的，因为我们有一部分点没有回退，我们可以尝试根据这个解再去回退一部分的带点，得到一个新解，这个解显然相对于原来的解是更优的，但还是可能不是最优的。那我们就继续回退，不断迭代，直到我们的答案稳定下来为止。
但这样可能会迭代很多次，总次数是$O\left(nB\right)$级别的，再配上我们单次计算就会达到$O\left(n^{2}B\right)$的时间复杂度，显然会T。

但我们发现我们上面的做法其实有一个特点，如果我们当前的解大于我们本来的解，它会减小。如果我们当前的解小于我们本来的解，可以发现它也是会增大的。
这就意味着我们可以二分我们的解，观察一次迭代后它的变化趋势，如果变大就意味着我们小了，否则就大了。
这样就可以二分出我们的答案。
注意原题保证的答案$⩽10^6$就无解事实上是指答案大于$10^6$时就把它看成无解，输出$-1$，所以我们可以将右边界设为$10^6+1$，这样就可以知道最后答案是不是$>10^6$。
我可以先跑一遍检验是否无解。

时间复杂度$O\left(n^{2}B\log Ans\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const double eps=1e-9;
template<typename _T>
void read(_T &x)
	_T f=1;x=0;char s=getchar();
	while(s<'0'||s>'9')if(s=='-')f=-1;s=getchar();
	while('0'<=s&&s<='9')x=(x<<3)+(x<<1)+(s^48);s=getchar();
	x*=f;

template<typename _T>
_T Fabs(_T x)return x<0?-x:x;
int add(int x,int y,int p)return x+y<p?x+y:x+y-p;
void Add(int &x,int y,int p)x=add(x,y,p);
int qkpow(int a,int s,int p)int t=1;while(s)if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;return t;
int n,m,H,deg[105],dg[105],maxx[105],val[105],ord[105],idx;
double dp[105][105][2],gp[105][105][2],fp[105][105];
bool vis[105][105];
vector<int>G[105],P[105];
queue<int>q;
int main()
	//freopen("kancolle.in","r",stdin);
	//freopen("kancolle.out","w",stdout);
	read(n);read(m);read(H);clock_t startt=clock();
	for(int i=1,u,v;i<=m;i++)
		read(u),read(v),G[u].pb(v),P[v].pb(u),deg[u]++;
	for(int i=1;i<=n;i++)read(val[i]);
	for(int i=1;i<=n;i++)
		int siz=G[i].size();
		for(int j=0;j<siz;j++)
			maxx[i]=max(maxx[i],val[G[i][j]]);
	
	for(int i=1;i<=H;i++)dp[n][i][1]=1;
	for(int i=1;i<=n;i++)dg[i]=deg[i];
	for(int i=1;i<=n;i++)if(!dg[i])q.push(i);
	while(!q.empty())
		int u=q.front();q.pop();ord[++idx]=u;
		if(u^n)
			if(!deg[u])for(int i=1;i<=H;i++)dp[u][i][0]=1,gp[u][i][0]=H-i;
			else
				int siz=G[u].size();double tmp=1.0/deg[u];
				for(int i=1;i<=maxx[u];i++)
					dp[u][i][0]=1,gp[u][i][0]=H-i;
				for(int i=maxx[u]+1;i<=H;i++)
					for(int j=0;j<siz;j++)
						int v=G[u][j];
						dp[u][i][0]+=tmp*dp[v][i-val[v]][0];
						dp[u][i][1]+=tmp*dp[v][i-val[v]][1];
					
					for(int j=0;j<siz;j++)
						int v=G[u][j],t=i-val[v];
						if(dp[u][i][0]>eps)gp[u][i][0]+=tmp*dp[v][t][0]/dp[u][i][0]*(gp[v][t][0]+1);
						if(dp[u][i][1]>eps)gp[u][i][1]+=tmp*dp[v][t][1]/dp[u][i][1]*(gp[v][t][1]+1);
					
				
			
		
		int siz=P[u].size();
		for(int i=0;i<siz;i++)
			int v=P[u][i];dg[v]--;
			if(!dg[v])q.push(v);
		
	
	if(dp[1][H][1]<eps)puts("-1");return 0;
	double tmp=gp[1][H][1]+dp[1][H][0]*gp[1][H][0]/(1.0-dp[1][H][0]); 
	for(int i=2;i<idx;i++)
		for(int j=1,x=ord[i];j<=H;j++)
			fp[x][j]=dp[x][j][1]*gp[x][j][1]+dp[x][j][0]*(gp[x][j][0]+tmp);
	double l=0,r=1e6+1;int times=60;
	while(times--)
		double mid=(l+r)/2.0;tmp=mid;
		for(int i=1;i<=idx;i++)
			int x=ord[i];if(x==1||x==n)continue;
			if(!deg[x])for(int j=1;j<=H;j++)fp[x][j]=H-j+tmp;continue;
			for(int j=1;j<=maxx[x];j++)fp[x][j]=H-j+tmp;
			double tp=1.0/deg[x];int siz=G[x].size();
			for(int j=maxx[x]+1;j<=H;j++)
				fp[x][j]=0;
				for(int k=0;k<siz;k++)int v=G[x][k];fp[x][j]+=tp*(fp[v][j-val[v]]+1);
				fp[x][j]=min(tmp+H-j,fp[x][j]);
			 
		
		int siz=G[1].size();double tp=1.0/deg[1];tmp=0;
		for(int k=0;k<siz;k++)int v=G[1][k];tmp+=tp*(fp[v][H-val[v]]+1);
		if(tmp>mid)l=mid;else r=mid;
	
	if(l>1e6)puts("-1");else printf("%.9f\\n",l);
	return 0;