[概率论与数理统计-1]: 总体架构知识结构知识体系

Posted 2022-03-28 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123751092

---

目录

第1章 基础概念与层次架构

1.1 概率与数理统计

1.2 概率论

1.3 数理统计

1.4 概率与数理统计的异同

1.5 概率论主要概念的层次架构

1.6 概率论与数理统计的基础知识章节顺序

第2章 概率基础

2.1 概率

2.2 概率分布

第3章 数理统计基础

3.1 表格与图形法

3.2 数值法

第4章 概率与统计的高阶知识

4.1 残差

4.2 拟合优化

4.3 多元回归

4.4 非参数方法

4.5 回归分析

4.6 假设检验

4.7 简单线性回归

4.8 均值

4.9 区间估计

4.10 事件序列分析与预测

4.11 实验实际与方差

第5章总结与感悟

参考：

---

---

第1章 基础概念与层次架构

1.1 概率与数理统计

《概率论和数理统计》是高等院校理工类、经管类的重要课程之一。主要内容包括：概率论的基本概念、随机变量及其概率分布、数字特征、大数定律与中心极限定理、统计量及其概率分布、参数估计和假设检验、回归分析、方差分析、马尔科夫链等内容。

1.2 概率论

概率论，是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的，在一定条件下必然发生某一结果的现象称为决定性现象。例如在标准大气压下，纯水加热到100℃时水必然会沸腾等。随机现象则是指在基本条件不变的情况下，每一次试验或观察前，不能肯定会出现哪种结果，呈现出偶然性。例如，掷一硬币，可能出现正面或反面。随机现象的实现和对它的观察称为随机试验。随机试验的每一可能结果称为一个基本事件，一个或一组基本事件统称随机事件，或简称事件。典型的随机试验有掷骰子、扔硬币、抽扑克牌以及轮盘游戏等。

事件的概率是衡量该事件发生的可能性的量度。虽然在一次随机试验中某个事件的发生是带有偶然性的，但那些可在相同条件下大量重复的随机试验却往往呈现出明显的数量规律

1.3 数理统计

数理统计是数学的一个分支，分为描述统计和推断统计。

它以概率论为基础，研究大量随机现象的统计规律性。

数理统计包括抽样、适线问题、假设检验、方差分析、相关分析等内容。抽样检验是要通过对子样的调查，来推断总体的情况。究竟抽样多少，这是十分重要的问题，因此，在抽样检查中就产生了“小样理论”，这是在子样很小的情况下，进行分析判断的理论。

描述统计：其任务是搜集资料，进行整理、分组，编制次数分配表，绘制次数分配曲线，计算各种特征指标，以描述资料分布的集中趋势、离中趋势和次数分布的偏斜度等。

推断统计：是在描述统计的基础上，根据样本资料归纳和统计出的规律性，对总体进行推断和预测。

1.4 概率与数理统计的异同

数理统计是构建在概率论基础之上的。

概率论是在数理统计内在原理的总结、提炼和概括的结论。

在概率论中，所研究的随机变量，其分布都是假设已知的，在这一前提下去研究它的性质、特点、规律，如数字特征、随机变量的函数分布。

在数理统计中，所研究的随机变量，其分布是未知的或者是不完全知道的，通过对所研究的随机变量进行重复独立的观察，得到的观察值，对这些数据进行分析，从而对所研究的随机变量的分布做出种种推断（这不就是机器学习模型与训练吗）。

所以数理统计是比概率论更高一个层次的内容，所以教材的名称也是概率论与数理统计，先讲概率论后讲数理统计。

1.5 概率论主要概念的层次架构

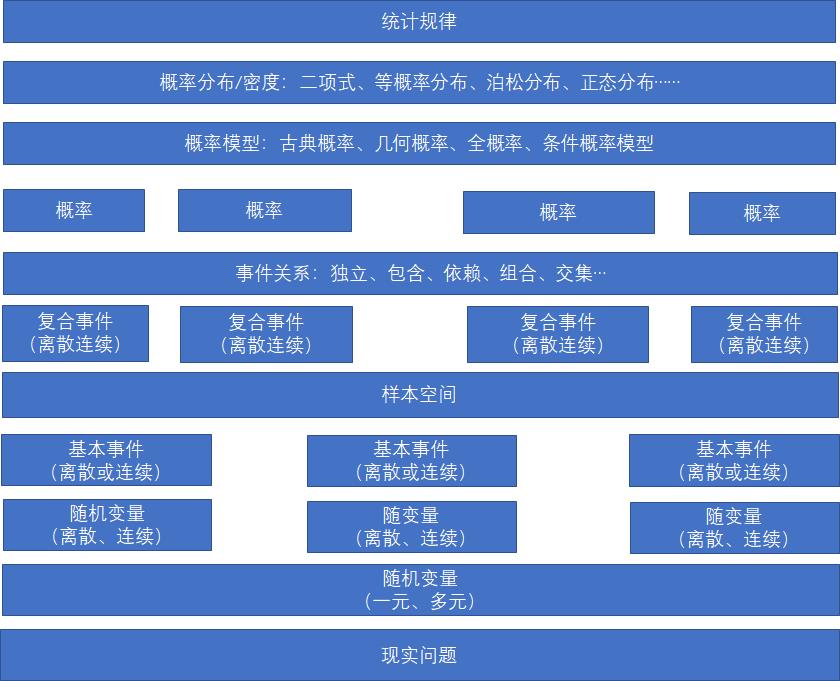
 事件组成：基本事件-》复合事件 -》 样本空间

事件有基本事件，也可以有复合事件，复合事件有多事件组合而成，复合可以是一元随机变量的多个事件组合而成，也可以是有多元随机变量的多个事件组合而成。

事件关系：独立关系、先后依赖关系关系、包含关系、相交关系、组合关系等等。

随机变量：一元随机变量、多元随机变量，每个随机变量都有各自的事件组成，而不同随机变量的事件之间可以是独立的，也可以是依赖关系。

概率：某个事件出现的可能性大小就是概率，是【0,1】之间的某个数，它可以是基本事件的可能性，也可以是复合事件的可能性，可以是一元随机变量的事件的可能性，也可能是多个随机变量组成的符合事件的可能性。

1.6 概率论与数理统计的基础知识章节顺序

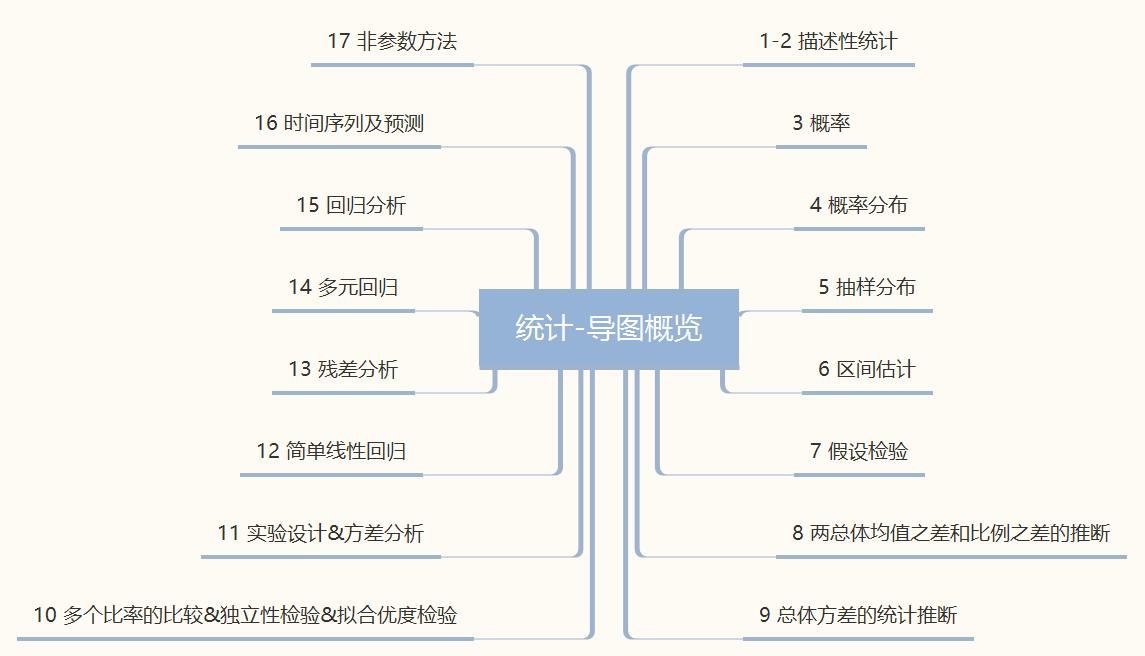
第2章 概率基础

2.1 概率

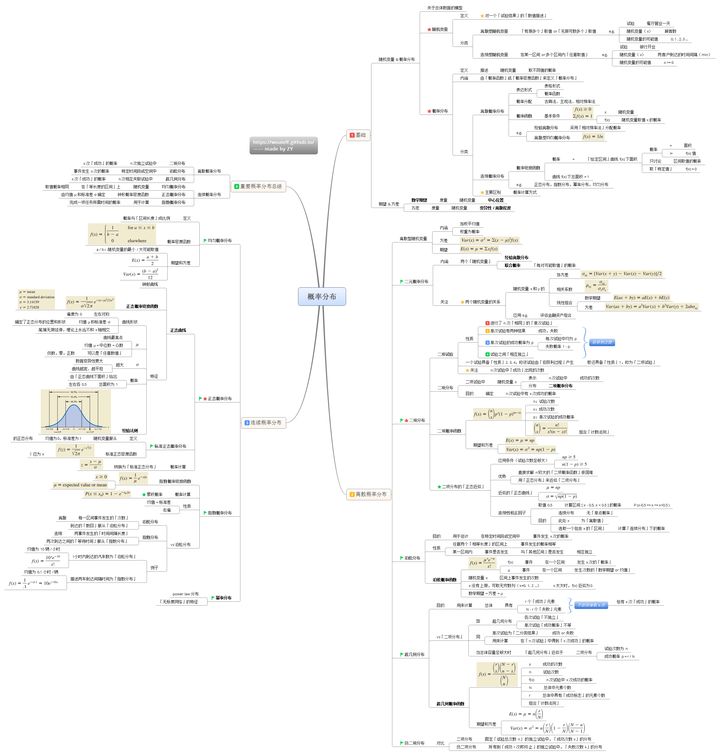
2.2 概率分布

第3章 数理统计基础

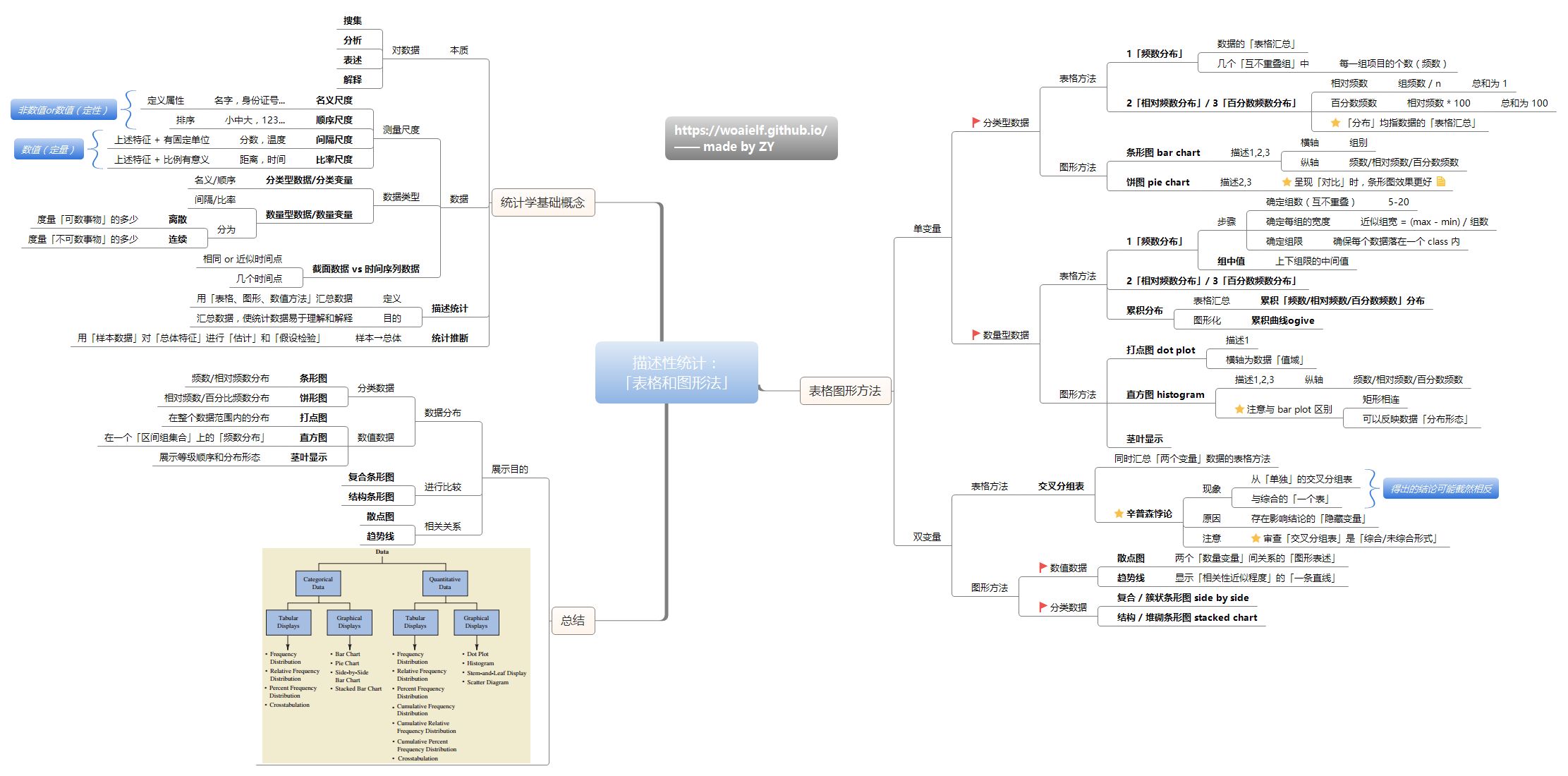
3.1 表格与图形法

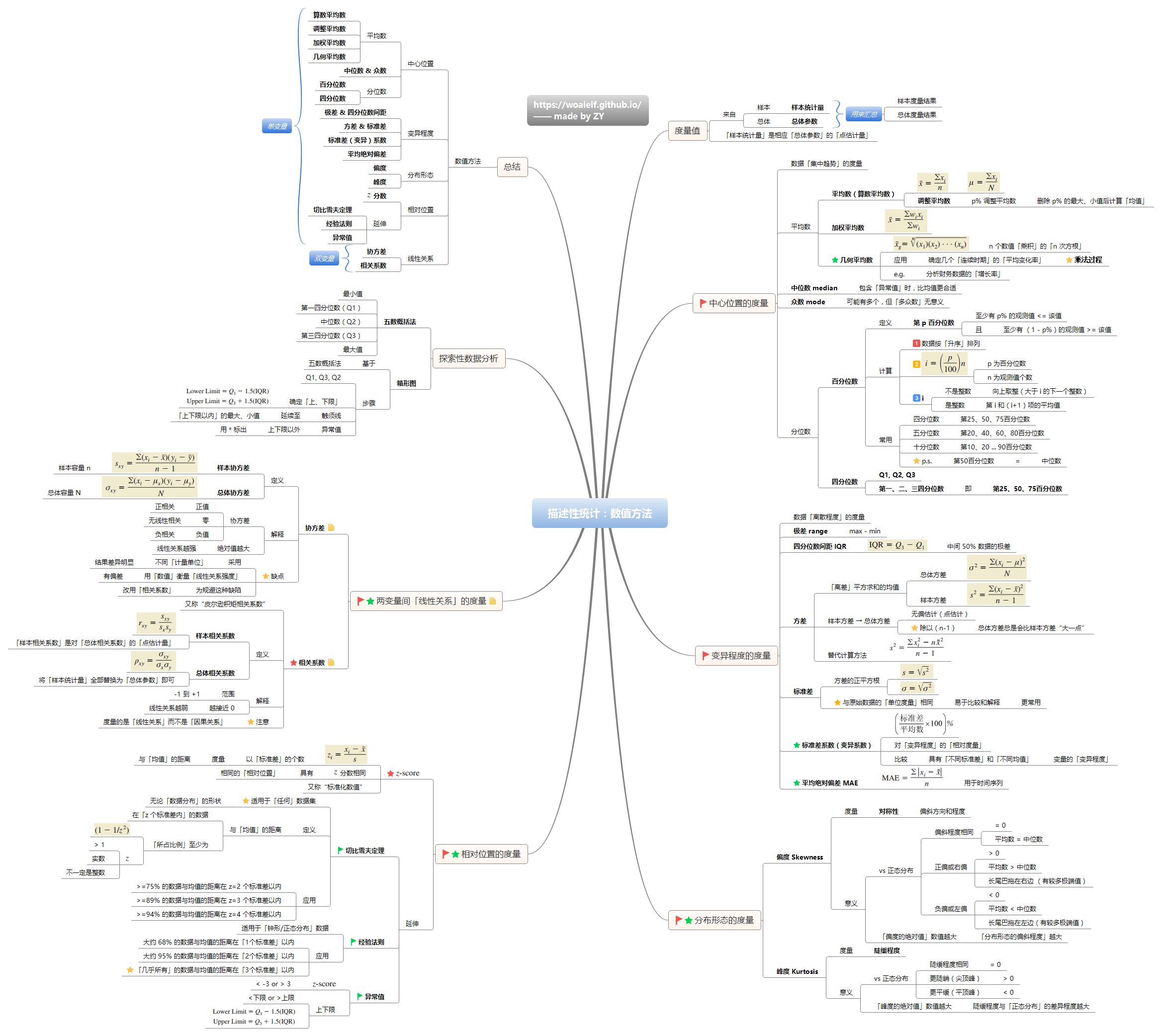
3.2 数值法

第4章 概率与统计的高阶知识

4.1 残差

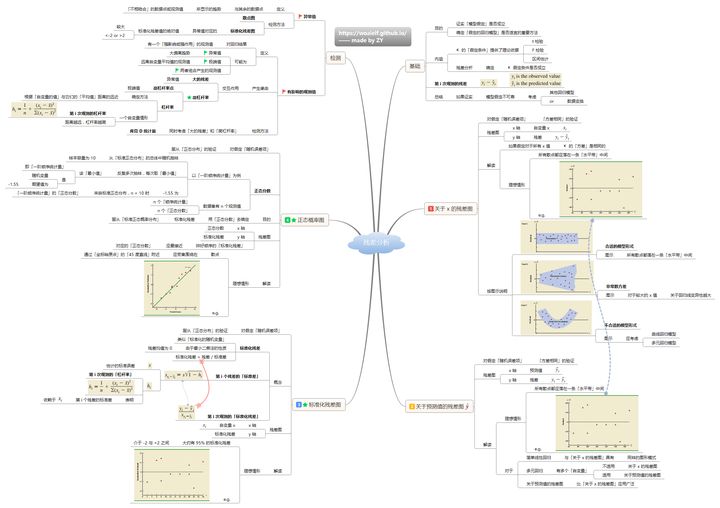
4.2 拟合优化

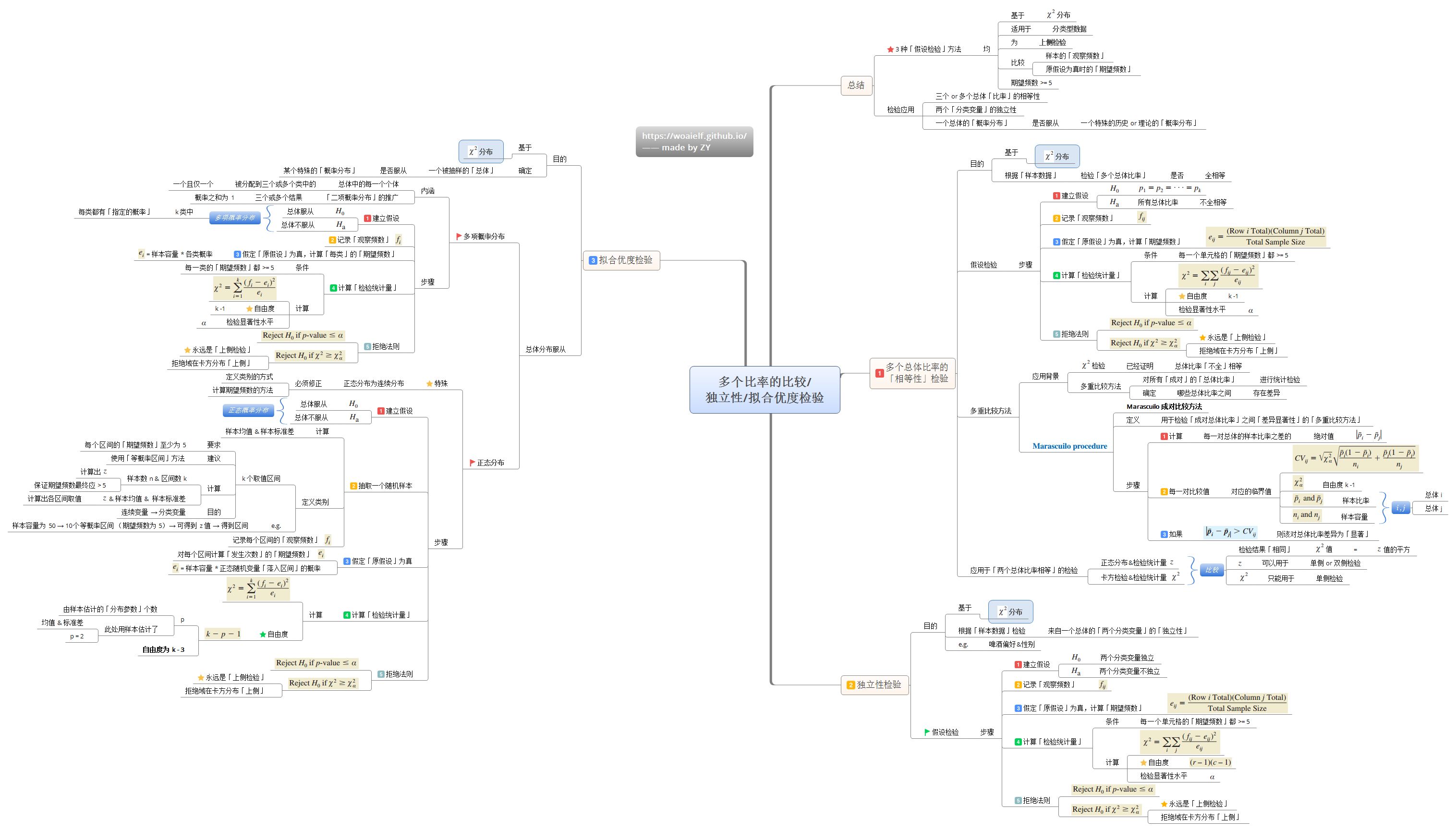
4.3 多元回归

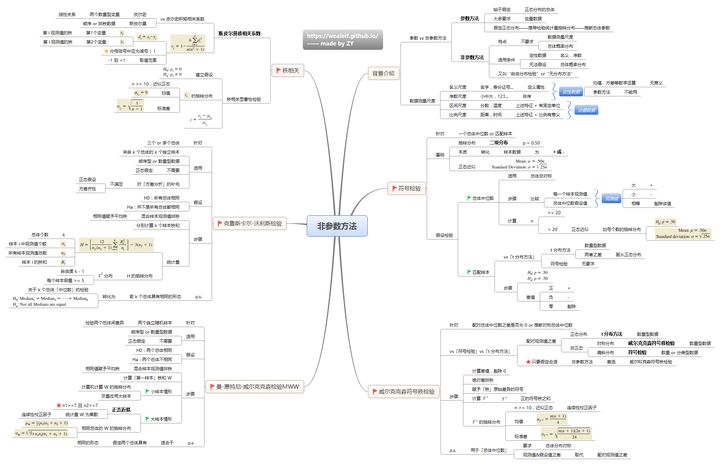
4.4 非参数方法

4.5 回归分析

4.6 假设检验

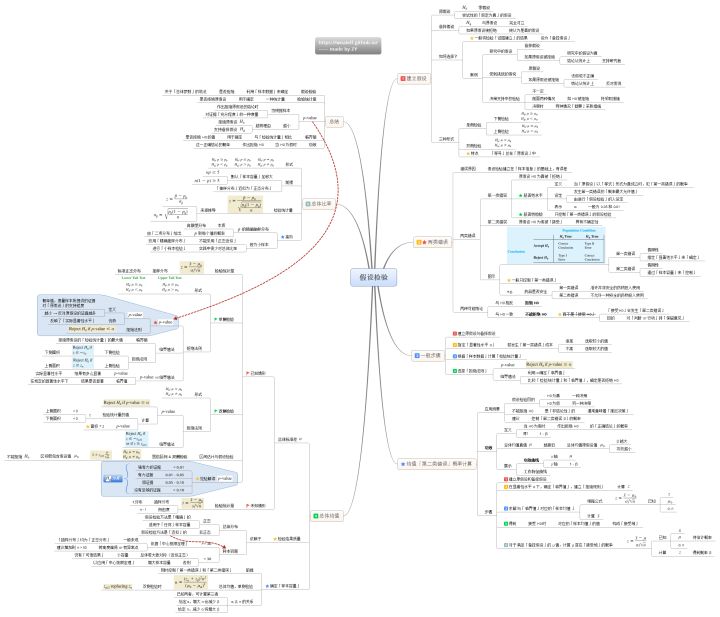
4.7 简单线性回归

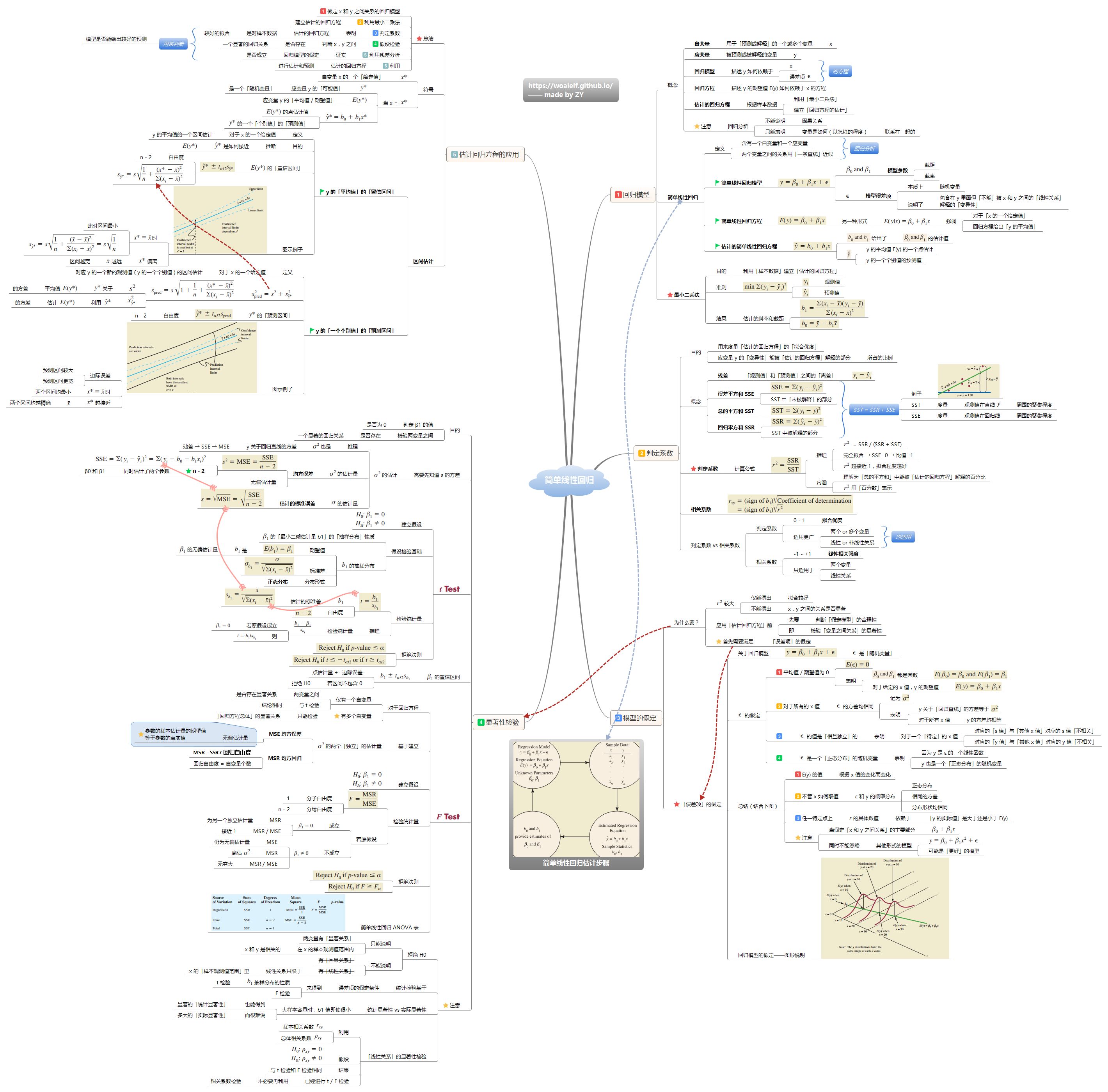
4.8 均值

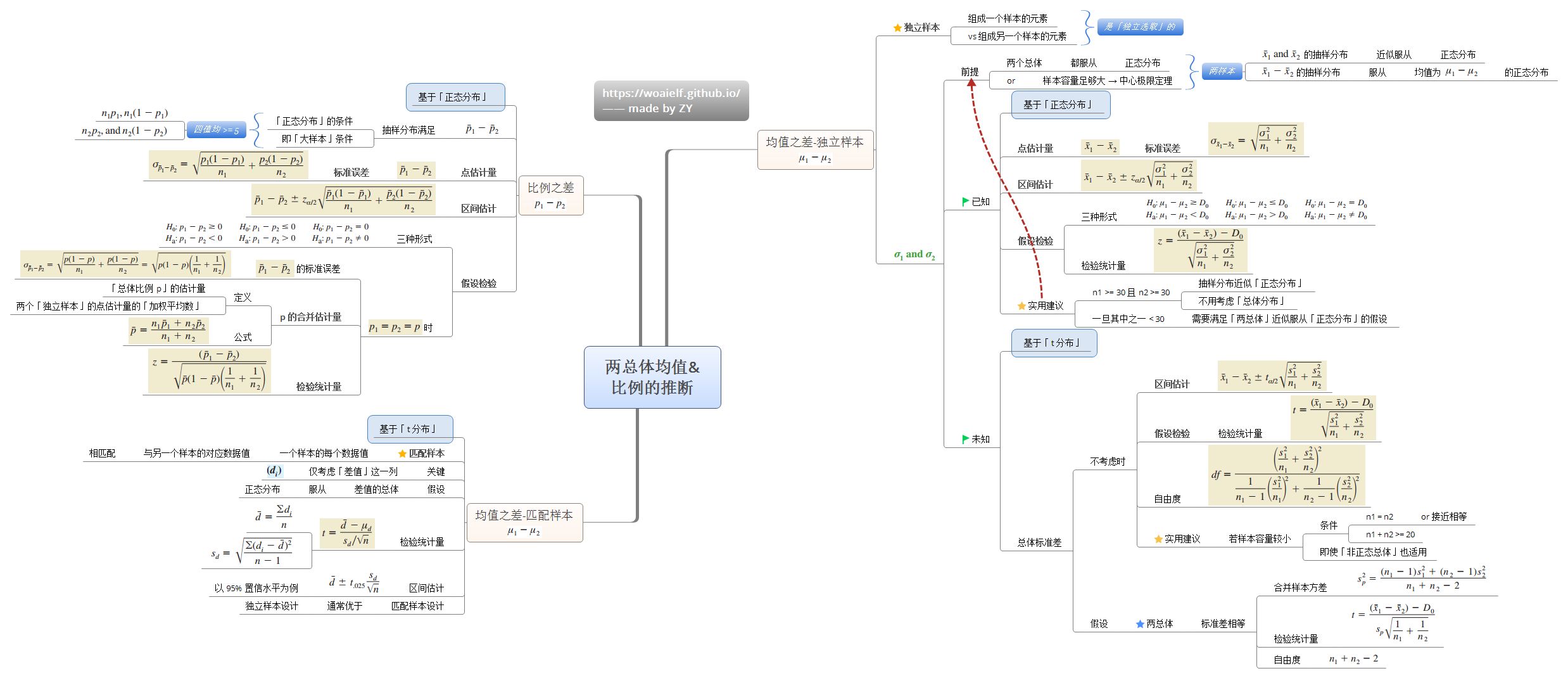
4.9 区间估计

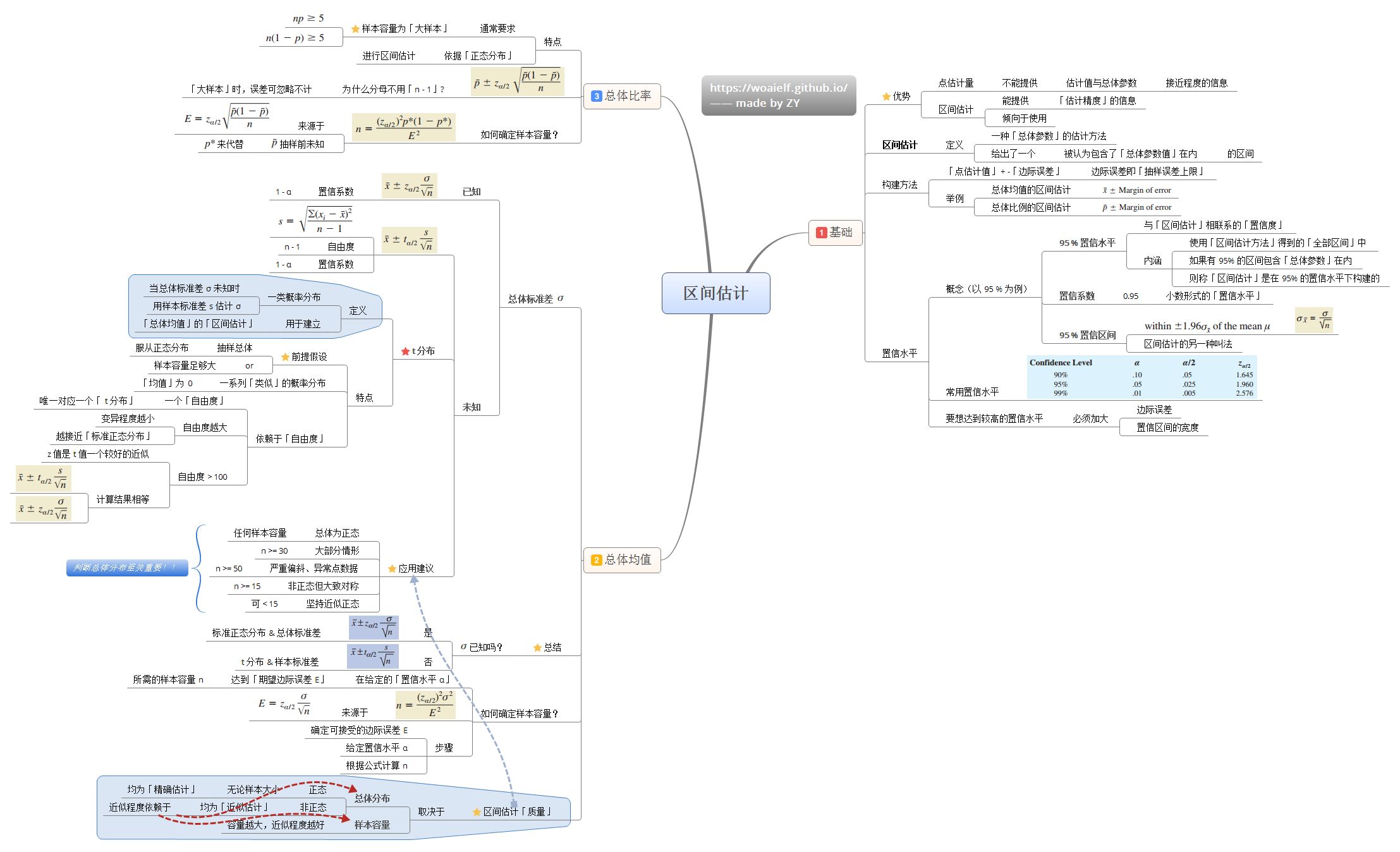
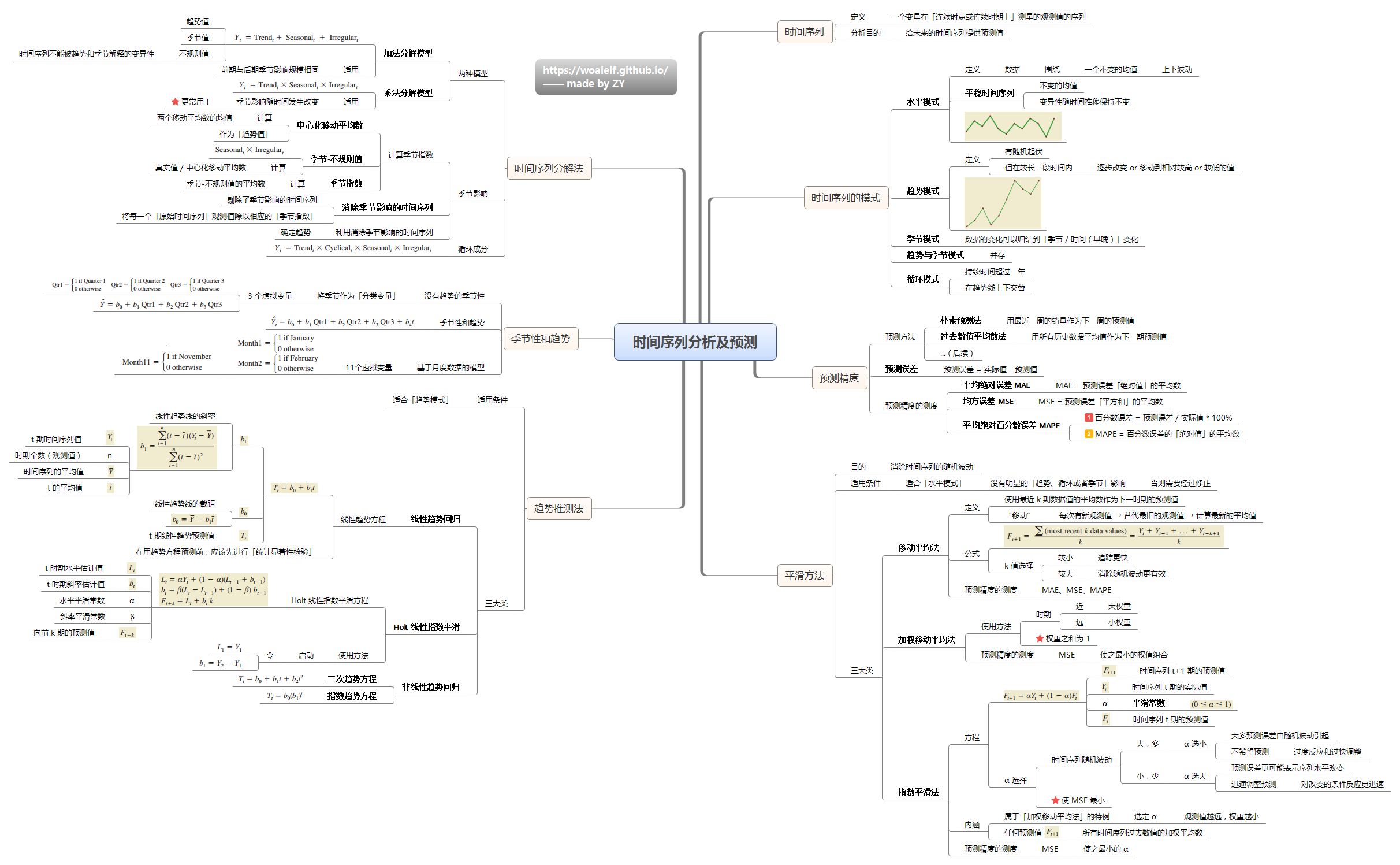
4.10 事件序列分析与预测

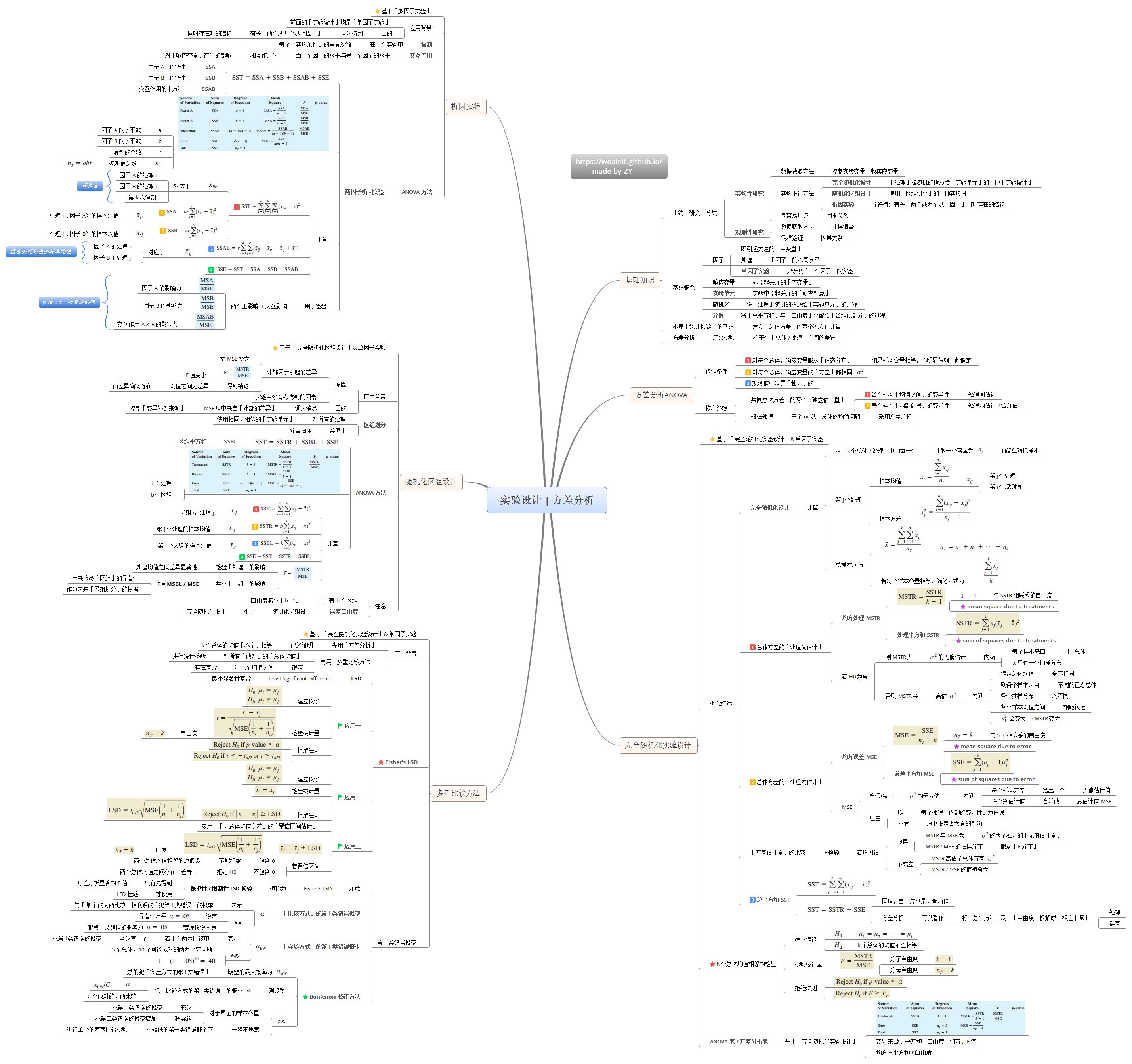
4.11 实验实际与方差

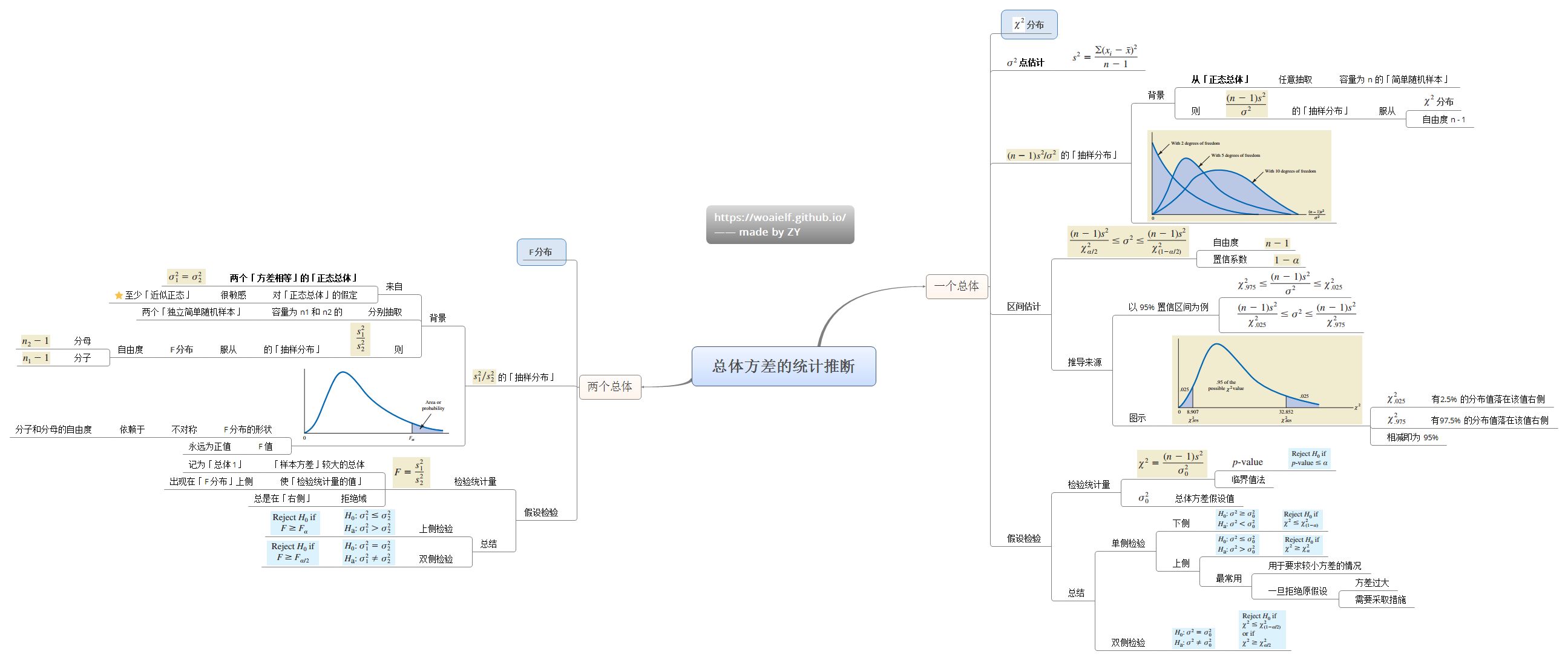
第5章总结与感悟

（1）将概率论的知识应用于生活中。

学以致用才是理解一门学科的最有效途径，生活中的各种交通工具风险概率、赌博的独立事件、保险的意义等等问题，实际上都与概率论有着重要联系。如果在生活中碰到问题能将这些问题透过现象看本质，将其看成是个概率问题，也是为生活提供了另一个观察的视角，做个明白人。

（2）概率论的知识一定要多用软件联系。

通过phthon和scikit-learn或excel表格，随时把概念转换为代码和图形化展示，对于概率的理解非常有帮助。

---

参考：

概率论知识总结梳理 - 知乎

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123751092