程序员的数学概率论

Posted 2022-03-28 辰chen

目录

• 前言
• 一、概率论与机器学习
• 二、随机事件
• 三、条件概率
• • 3.1 条件概率公式
  • 3.2 贝叶斯公式
• 四、随机事件独立性
• 五、随机变量
• • 5.1 离散随机变量
  • 5.2 连续随机变量
  • 5.3 概率密度函数概率计算
• 六、数学期望与方差
• • 6.1 期望
  • 6.2 方差
  • 6.3 重要公式
• 七、随机向量
• 八、随机变量独立性
• 九、协方差
• 十、机器学习中常见分布
• 十一、最大似然估计

前言

本文其实值属于：程序员的数学【AIoT阶段二】 （尚未更新）的一部分内容，本篇把这部分内容单独截取出来，方便大家的观看，本文介绍 概率论，本文涵盖了一些计算的问题并使用代码进行了实现，安装代码运行环境见博客：最详细的Anaconda Installers 的安装【numpy，jupyter】（图+文），如果你只是想要简单的了解有关线代的内容，那么只需要学习一下博文：NumPy从入门到高级，如果你是跟着博主学习 $AIoT$ 的小伙伴，建议先看博文：数据分析三剑客【AIoT阶段一（下）】（十万字博文 保姆级讲解），如果你没有 $Python$ 基础，那么还需先修博文：Python的进阶之道【AIoT阶段一（上）】（十五万字博文 保姆级讲解）

一、概率论与机器学习

🚩机器学习其实是集合了统计学、概率论、计算机科学、数学算法等方面的交叉研究，即便你对机器学习的应用炉火纯青，但对这些技术没有一个全面的数学理解，极有可能出现应用失误。因此与其说为什么概率论与数理统计在机器学习中为什么这么重要，不如说为什么数学在机器学习中为什么这么重要！

概率论研究的是事物的不确定性，它是统计学、信息论的前置课程。概率论的难度系数属中等，毕竟你在高中就学习过如何计算一个随机变量的期望、方差。从机器学习的视角来看，概率论是必须要了解的，但不需要达到精通的程度。你只需要灵活运用它，把机器学习世界的不确定性变量算清楚就足够了。因此，当你掌握了概率论，你就揭开机器学习世界神秘的一层面纱。

对于有监督机器学习，其属性特征数据对应 $X$，它的目标值标签对应 $y$，如果我们把它当作是随机变量的话，那我们就可以用概率论的观点对它进行建模。假设它服从某种概率分布，比如说人的身高大体是服从正太分布的，像姚明一样非常高的非常少，像郭敬明一样矮也是非常少的，比如中国的男性平均身高 $1.75$ 左右，画出来就是我们学概率论和数理统计时候的一个正太分布：

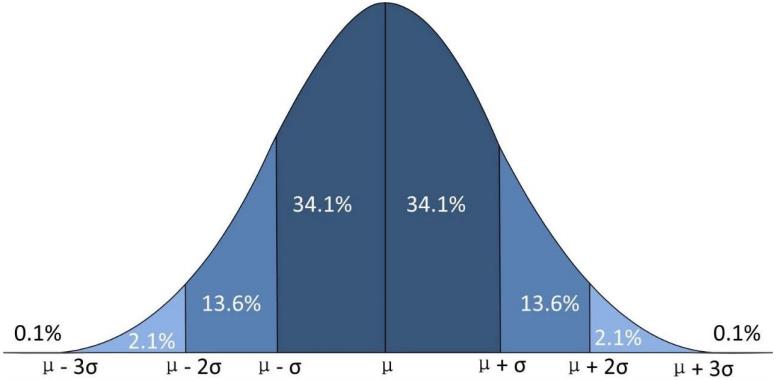
我们要是对数据进行分类的话，根据他的身高、体重等等，那我们就可以对他的身高进行建模来计算它服从某种分布，然后计算他的概率，这就是我们要学习概率论的原因。

二、随机事件

🚩什么是随机事件呢？ 就是可能发生，也可能不发生的事件。比如你抛硬币，它正面朝上或者反面朝上，这就是一个随机事件；生孩子，生男生女这也是一个随机事件。

如果一定发生的话，这种称为必然事件，比如说太阳明天会升起，这肯定是必然事件；不可能发生的事件，我们称之为不可能事件，比如水往高处流，这就是不可能事件。

我们一般把随机事件用大写字母 $A$ 或 $B$ 这样来表示，每一个随机事件它关联有一个发生的概率，记作 $P(A)$，像抛硬币它正面朝上的概率是 $0.5$，反面朝上的概率也是 $0.5$，$0\le P(A)\le 1$。 如果概率等于 $1$ 那就是必然事件，如果等于 $0$ 那就是不可能事件。以前学概率论时，老师交了我们各种计算概率的方法，比如抽各种颜色的球等等这样的问题，一般都是用排列组合来算的。

三、条件概率

3.1 条件概率公式

🚩条件概率是针对于两个或更多个有相关关系、因果关系的随机事件而言的。对于两个随机事件 $A$ 和 $B$ 而言，在 $A$ 发生的情况下 $B$ 发生的概率，那记作 $P(B|A)$，即 $AB$ 同时发生的概率除以 $A$ 发生的概率：$P(B|A)=\frac{P(AB)}{P(A)}$

同理，在 $B$ 发生的情况下 $A$ 发生的概率，那记作 $P(A|B)$

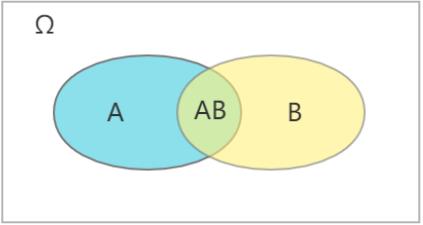
$\Omega$ 表示样本空间，即表示全部事件。

3.2 贝叶斯公式

🚩根据条件概率公式，可以推导出贝叶斯公式：

$P(B)P(A|B)=P(AB)P(B|A)$
$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$

贝叶斯公式得到的结果是后验概率，后验概率是指依据得到’'结果"信息所计算出的最有可能是那种事件发生，如贝叶斯公式中的, 是"执果寻因"问题中的"因"。

举例说明：餐桌上有一块肉和一瓶醋，你如果吃了一块肉，很酸，那你觉得肉里加了醋的概率有多大？你说：$80\%$ 可能性加了醋。$OK$，你已经进行了一次后验概率的猜测，没错，就这么简单！这就是"执果寻因"。

贝叶斯公式在整个机器学习和深度学习中是非常有用的，因为很多时候我们要用一种叫做最大化后验概率（$Maximum$ $a$ $posterioriestimation$，简称 $MAP$）的思想。

四、随机事件独立性

🚩说白了就是两个事情是不相关的， $B$ 在 $A$ 发生的条件下发生的概率是等于 $B$ 本身发生的概率：

$P(B|A)=P(B)$
$P(AB)=P(A)P(B)$

我们可以把它推广到 $n$ 个事件相互独立的情况上面去，就是等于各自发生概率的乘积：

$P(a_1,a_2,...,a_n)=\prod _{i=1}^{n}P(a_i)$

五、随机变量

🚩整个概率论的核心。变量是什么呢？

我们中学的时候就学习过变量了，它是取值可以变化的量，比如可以取 $0$ 到 $1$ 区间上所有的实数，或者取从 $1$ 到 $100$ 之间的整数。

5.1 离散随机变量

🚩随机变量是什么呢？

就是变量取值都有一个概率。第一种情况是离散型的随机变量，比如前面说的抛硬币正面朝上还是反面朝上，这是两个事件，我们可以把这两个事件编号，得到：

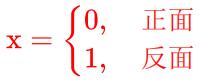
这就是随机变量，$x$ 取值有两种情况，$0$ 或 $1$，取每种值的概率都是 $0.5$，离散型的随机变量它的取值只可能是有限可能个，像掷色子，就有 $6$ 中可能 $（1、2、3、4、5、6）$，取每种值的概率都是 $\frac{1}{6}$；或者无穷可列个，比如，$1$ 到 $+\infty$，虽然是无穷个，但是一定可以用整数编号表示。

5.2 连续随机变量

🚩连续型的随机变量，理解起来抽象一些，它的取值是无限不可列个，比如 $0$ 到 $1$ 之间的所有的实数，首先它肯定是无限个，而它比无限可列个更高级，它不可列，比如其中的 $0.001$ 到 $0.002$ 之间还是有无限个，不管怎么细分，$a$ 和 $b$ 之间还是有无限个，这就是连续型的随机变量，比如说抛石子在 $0$ 到 $1$ 的矩形范围内，它可能落在区域内任何一个位置，那么石子落在的位置 $x,y$ 就是连续型随机变量，说白了就是它坐标取 $0$ 到 $1$ 之间任何一个值都是有可能的。对于离散型随机变量，写成如下：

$P(x=x_i)=p_i$
$p_i\ge 0$
$\sum p_i=1$

对于连续型随机变量我们是这么定义的，利用它的概率密度函数来定义

$f(x)\ge 0$
${\int }_{-\infty }^{+\infty }f(x)dx=1$

通过概率密度函数可以计算事件发生的概率 $P(y)$，注意对于连续随机变量，往往计算区间的概率：

$P(y)=P(x\le y)=$