数据挖掘导论——分类与预测
Posted 上山打老虎D
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据挖掘导论——分类与预测相关的知识,希望对你有一定的参考价值。
数据挖掘导论——分类与预测
实验内容
背景介绍
泰坦尼克号于1909年3月31日在爱尔兰动工建造,1911年5月31日下水,次年4月2日完工试航。她是当时世界上体积最庞大、内部设施最豪华的客运轮船,有“永不沉没”的美誉。然而讽刺的是,泰坦尼克号首航便遭遇厄运:1912年4月10日她从英国南安普顿出发,途径法国瑟堡和爱尔兰昆士敦,驶向美国纽约。在14日晚23时40分左右,泰坦尼克号与一座冰山相撞,导致船体裂缝进水。次日凌晨2时20分左右,泰坦尼克号断为两截后沉入大西洋,其搭载的2224名船员及乘客,在本次海难中逾1500人丧生。
在该案例中,我们将探究什么样的人在此次海难中幸存的几率更高,并通过构建预测模型来预测乘客生存率。
数据
数据来源:根据blackboard上面提供的train.csv和test.csv文件。
字段说明:
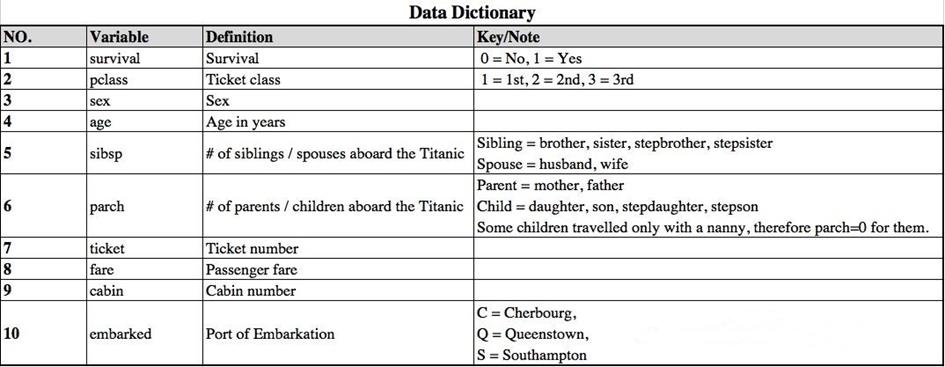
实验要求
1) 对缺失值和异常值进行处理;
2) 用Gradient Boosting Classifier和Logistic Regression模型进行建模;
3) 对比分析实验结果(评价指标包含Accuracy、Recall以及F1-score等)。
实验过程
一、首先引入数据分析以及模型所需要的库
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
from IPython.display import display
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics ,ensemble
二、进行数据的读取
使用pandas.read_csv将数据读入。并查看前几个数据
data=pd.read_csv("train.csv")
data.head()

三、进行数据分析
首先,对缺失值进行统计
data.isnull().sum()

可以看到,数据中存在比较多的缺失值,需要进一步填充处理。接下来,查看整体数据情况。
data.describe()
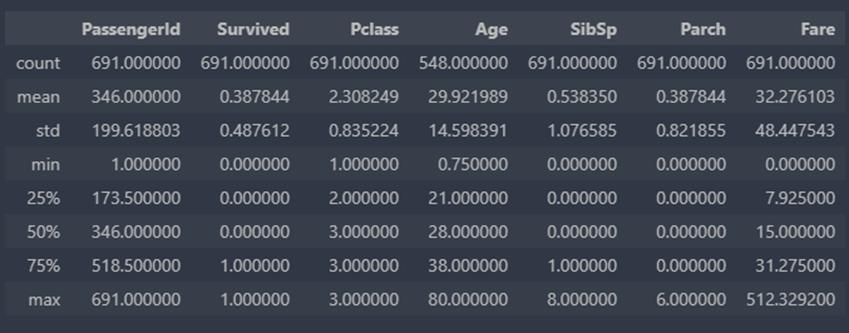
获取整体乘客中获救乘客的比例
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
sns.countplot('Survived',data=data,ax=ax[1])
ax[1].set_title('Survived')
plt.show()

可以看到,在这次事故中,并没有多少乘客幸免于难。在训练集的691名乘客中,只有大约270人幸存下来(38.8%)。
我们需要从数据中提取出更多的信息用以模型的构建,接下来,我们将尝试使用数据集的不同特性进行检查与分析。
1、Sex:性别比例
data.groupby(['Sex','Survived'])['Survived'].count()
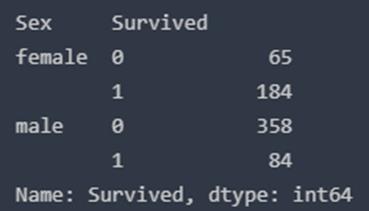
图形表示:
f,ax=plt.subplots(1,2,figsize=(18,8))
data[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
sns.countplot('Sex',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Sex:Survived vs Dead')
plt.show()
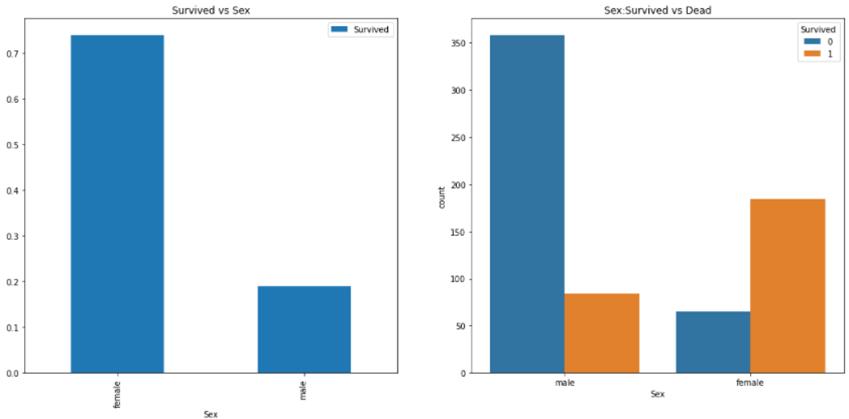
不难发现船上的男人比女人多得多。不过,挽救的女性人数几乎是男性的两倍。生存率为一个女人在船上是75%左右,而男性在18-19%左右。
这是建模的一个非常重要的特性。
2、PClass:船舱等级
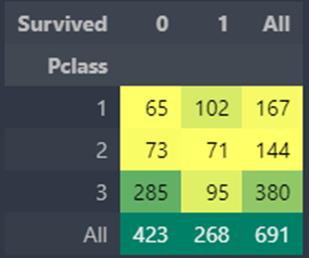
pd.crosstab(data.Pclass,data.Survived,margins=True).style.background_gradient(cmap='summer_r')
图形表示
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Pclass'].value_counts().plot.bar(color=['#CD7F32','#FFDF00','#D3D3D3'],ax=ax[0])
ax[0].set_title('Number Of Passengers By Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Pclass:Survived vs Dead')
plt.show()

可以发现:船舱等级为1的被给予很高的优先级而救援。尽管数量在pClass 3乘客高了很多,仍然他们的存活率是非常低的,大约25%。对于pClass1来说存活率是63%左右,而pclass2大约是48%。
3、PClass,Sex:船舱等级与性别
pd.crosstab([data.Sex,data.Survived],data.Pclass,margins=True).style.background_gradient(cmap='summer_r')

图形表示
sns.factorplot('Pclass','Survived',hue='Sex',data=data)
plt.show()
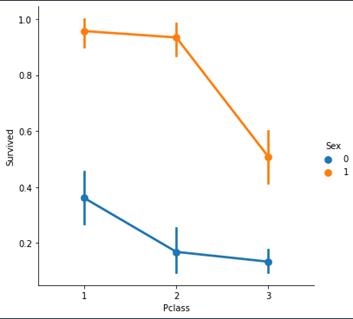
我们用factorplot生成这个图,看起来更直观一些。我们可以很容易地推断,从pclass1女性生存是95-96%,只有3%的女性从pclass1没获救。显而易见的是,不论pClass,女性优先考虑。
4、Age:年龄
print('Oldest Passenger was of:',data['Age'].max(),'Years')
print('Youngest Passenger was of:',data['Age'].min(),'Years')
print('Average Age on the ship:',data['Age'].mean(),'Years')

图形表示
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=data,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=data,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()

可以发现,20-60岁的乘客获救几率更高一些,对于男性来说,二十五岁以后的男性随着年龄的增长,存活率降低。
【缺失值填充】
可以发现,年龄特征存在很多空值,我们需要填补这些空值以便进行预测。为了替换这些空值,我们可以给他们分配数据集的一些平均年龄。通过检查姓名特征(先生,夫人等称呼)可以乘客进行合理分组,这样分组填补将使预测更加准确。
data['Initial']=0
for i in data:
data['Initial']=data.Name.str.extract('([A-Za-z]+)\\.')
这里我们使用正则表达式对信息进行匹配提取
图形化
pd.crosstab(data.Initial,data.Sex).T.style.background_gradient(cmap='summer_r') #用性别核对姓名首字母

data['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr'],inplace=True)
data.groupby('Initial')['Age'].mean()

接下来对缺失值进行填充
data.loc[(data.Age.isnull())&(data.Initial=='Mr'),'Age']=33
data.loc[(data.Age.isnull())&(data.Initial=='Mrs'),'Age']=36
data.loc[(data.Age.isnull())&(data.Initial=='Master'),'Age']=5
data.loc[(data.Age.isnull())&(data.Initial=='Miss'),'Age']=22
data.loc[(data.Age.isnull())&(data.Initial=='Other'),'Age']=46
data.Age.isnull().any() #看看填充结果

完成填充之后,查看填充的结果
f,ax=plt.subplots(1,2,figsize=(20,10))
data[data['Survived']==0].Age.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('Survived= 0')
x1=list(range(0,85,5))
ax[0].set_xticks(x1)
data[data['Survived']==1].Age.plot.hist(ax=ax[1],color='green',bins=20,edgecolor='black')
ax[1].set_title('Survived= 1')
x2=list(range(0,85,5))
ax[1].set_xticks(x2)
plt.show()

可以发现,幼儿获救数还是比较多的。年级最大的乘客获救了。死亡人数最多的是30-40年龄组
sns.factorplot('Pclass','Survived',col='Initial',data=data)
plt.show()
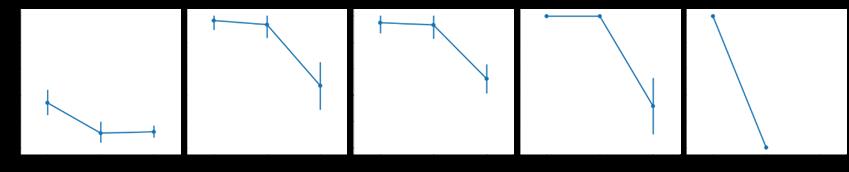
5、Embarked:登船地点
pd.crosstab([data.Embarked,data.Pclass],[data.Sex,data.Survived],margins=True).style.background_gradient(cmap='summer_r')
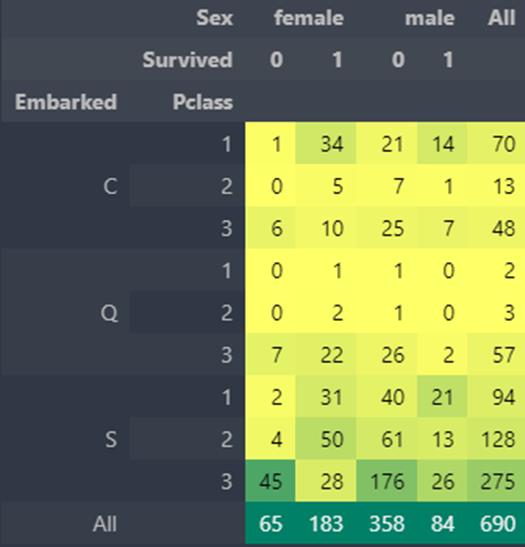
图形化
sns.factorplot('Embarked','Survived',data=data)
fig=plt.gcf()
fig.set_size_inches(5,3)
plt.show()
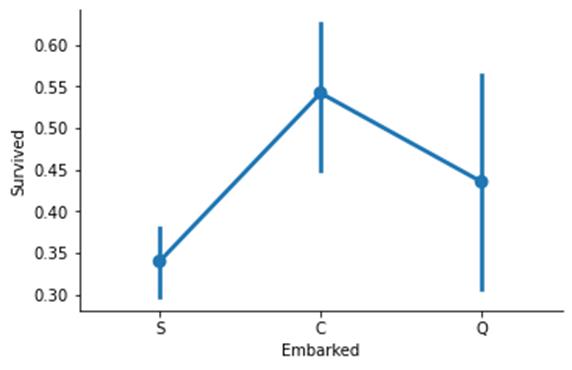
可以看出从C港上船的乘客的存活率最高,而从S港上船的乘客存活率最低。
不妨使用柱状图进行展示
f,ax=plt.subplots(2,2,figsize=(20,15))
sns.countplot('Embarked',data=data,ax=ax[0,0])
ax[0,0].set_title('No. Of Passengers Boarded')
sns.countplot('Embarked',hue='Sex',data=data,ax=ax[0,1])
ax[0,1].set_title('Male-Female Split for Embarked')
sns.countplot('Embarked',hue='Survived',data=data,ax=ax[1,0])
ax[1,0].set_title('Embarked vs Survived')
sns.countplot('Embarked',hue='Pclass',data=data,ax=ax[1,1])
ax[1,1].set_title('Embarked vs Pclass')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
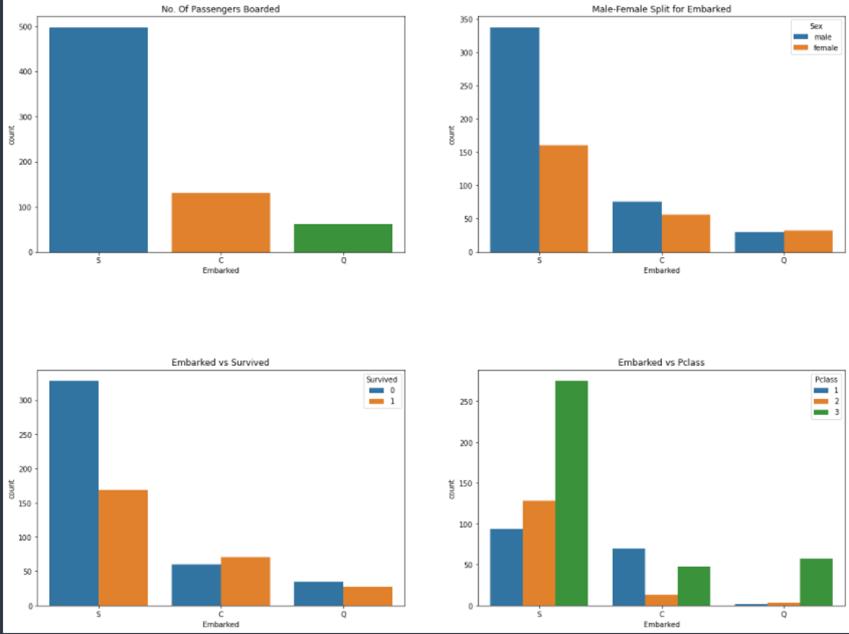
可以发现,大部分人的船舱等级是3。C港的乘客看起来很幸运,他们的存活率最高。
sns.factorplot('Pclass','Survived',hue='Sex',col='Embarked',data=data)
plt.show()
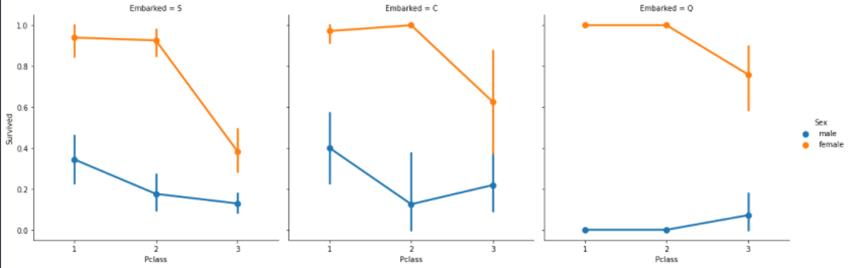
继续分析可以得出结论,存活率最高的是PClass1和PClass2的女人。PClass3的乘客中男性与女性的生存率都偏低。港口Q的乘客大部分都是PClass3
【缺失值填充】
港口信息也存在缺失值,此处,我们使用众数进行填充
data['Embarked'].fillna('S',inplace=True)
data.Embarked.isnull().any()

6、Sibsip:兄弟姐妹的数量
这个特征表示一个人是独自一人还是与他的家人在一起
pd.crosstab([data.SibSp],data.Survived).style.background_gradient(cmap='summer_r')

图形表示
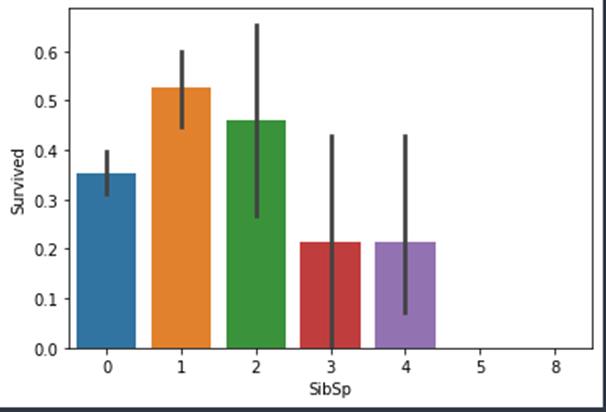

与PClass的关系
pd.crosstab(data.SibSp,data.Pclass).style.background_gradient(cmap='summer_r')

通过分析表明,如果乘客在船上没有兄弟姐妹,他有34.5%的存活率。但如果兄弟姐妹的数量增加,存活率或减少。不妨设想,这也是有道理的,生活中,当一个家庭在船上时,我们更倾向于去救助他们而不是救助自己。此外,我们也可以发现家庭成员数量在5-8的家庭的存活率为零,这或许跟他们处于PClass为3的船舱有关系。
7、Parch:
这个参数表示父母与孩子的数量
pd.crosstab(data.Parch,data.Pclass).style.background_gradient(cmap='summer_r')

图形化
sns.barplot('Parch','Survived',data=data)
sns.factorplot('Parch','Survived',data=data,ax=ax[1])
plt.show()
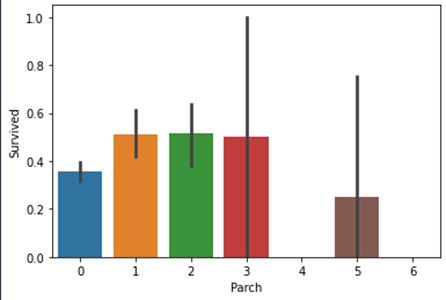

这再次表明,大家庭都在PClass3. 这里的结果也很相似。带着父母的乘客有更大的生存机会。然而,它随着数字的增加而减少。在船上的家庭父母人数中有1-3个的人的生存机会是好的。独自一人也证明是致命的,当船上有4个父母时,生存的机会就会减少。
8、Fare:船票的价格
船票的价格也可能是影响存活率的因素
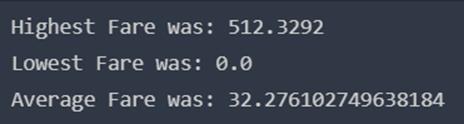
print('Highest Fare was:',data['Fare'].max())
print('Lowest Fare was:',data['Fare'].min())
print('Average Fare was:',data['Fare'].mean())
年龄与PClass以及存活率的关系:
f,ax=plt.subplots(1,3,figsize=(20,8))
sns.distplot(data[data['Pclass']==1].Fare,ax=ax[0])
ax[0].set_title(以上是关于数据挖掘导论——分类与预测的主要内容,如果未能解决你的问题,请参考以下文章