[机器学习与scikit-learn-36]:算法-分类-一元离散随机变量=>样本空间=>古典概率模型(事件自然数等概率均匀分布)
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-36]:算法-分类-一元离散随机变量=>样本空间=>古典概率模型(事件自然数等概率均匀分布)相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123724932
目录
第1章 一元随机变量的两个方面
1.1 随机变量
随机变量:首先是变量,其数值不是唯一的,是可变量。
随机变量:其二是随机,随机表明,变量的取值不是确定性,变量取某个数值有不同可能性的大小,这就是概率。
1.2 一元随机变量
当随机变量的个数只有一个时,称为一元随机变量,如X。
1.3 随机变量包含两个主要的方面:
(1)随机变量的所有取值范围 =》样本空间,样本空间的取值,有离散型的,也有连续性的。
(2)随机变量取某个数值的可能性的大小 =》 概率。
1.4 什么是概率模型
所谓概率模型,就是指随机变量的两个方面的所组织的特征,即概率模型要阐述随机变量的两个方面:
(1)样本空间:取值范围如何确定?
(2)概率与取值范围的对应关系: 如何求概率?
第2章 古典概率型
2.1 什么是古典概率
古典概型也叫传统概率、其定义是由法国数学家拉普拉斯 (Laplace ) 提出的。
如果一个随机试验所包含的单位事件是有限的,且每个单位事件发生的可能性均相等,则这个随机试验叫做拉普拉斯试验,这种条件下的概率模型就叫古典概型。
在这个模型下,随机实验所有可能的结果是有限的,并且每个基本结果发生的概率是相同的。
古典概型是概率论中最直观和最简单的模型,概率的许多运算规则,也首先是在这种模型下得到的。
2.2 古典概率如何问答随机变量的两个方面
(1)样本空间:取值范围如何确定?
古典概率型只强调了取值范围和个数是有限的,而不是无限的,至于如何确定样本空间中个数,古典概率本身并没有指明,需要用到其他概念,如:
- 排列
- 组合
排列和组合,都是用来计算,随机变量有多少种可能会出现的基本事件,所有可能性的基本事件,共同组合样本空间。
(2)概率与取值范围的对应关系: 如何求概率?
古典概率强调,每一种样本出现的“可能性”是相等的,即均匀分布的。因此,每一种样本出现的概率也是相等的,称为等概率模型。
具有以上两个特点的概率模型是大量存在的,这种概率模型称为古典概率模型,简称古典概型,也叫等可能概型。
(3)等概率随机分布函数--离散

(4)等概率随机分布函数--连续(无限个取值,不属于古典概率型)
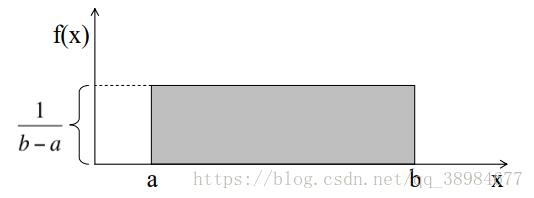
2.3 古典概率型判断的依据
有限性(所有可能出现的基本事件只有有限个)
等可能性(每个基本事件出现的可能性相等)
基本事件的特点
(1)任何两个基本事件是互斥的,或者说,各个事件是不相干的。
(2)任何事件(除不可能事件)都可以表示成基本事件的和。
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特征——有限性和等可能性,只有同时具备这两个特点的概型才是古典概型。
2.4 古典概率型的概率

要求随机变量每一个复合事件出现的概率,只需要求出样本空间中基本事件的个数和复合事件包含的基本事件的个数, 每个样本是等概率的,因此样本的概率就是包含的基本事件个数相除即可。
因此固定概率的核心是求符合事件的个数和样本空间中基本事件的个数,于是有了:
(1)排列
(2)组合
他们都是求样本空间中,所有基本事件的个数的。
第3章 排列组合
3.1 排列
(1)定义
排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当m=n时,这个排列被称作全排列(all permutation)。
m个元素,每一种排列类别,都称为一个事件。所有的可能的排列就是样本空间。

(2)排列与概率的关系
因此,每一种排列,出现的概率就是:1/P.
3.2 组合
(1)定义
组合(combination)是一个数学名词。一般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中取出m个元素的一个组合。我们把有关求组合的个数的问题叫作组合问题。

(2)与概率的关系
每一种出现的概率p= 1/C。
至于排列与组合自身的计算公式,不是本章的重点。
本章的重点是要阐述排列、组合与概率的关系,与样本空间的关系!!!!
3.3 事件的编码
排列和组合的是:用自然数标识的事件,事件的个数也用自然数表示,其样本空间实际是有限个自然数。
用自然数表示事件,每个自然数代表的是是一个事件。
也用自然数统计事件的总数。
把事件转换成自然数,用自然数表示事件,这是理解古典概率的关键点。
(1)比如,用0-9个数字进行排列,得到的样本就是:
0000000000, 0000000001,00000000002,.......9999999999。
每个串,都是一个事件,一共有10*10*10*10*10*10*10*10*10*10=10^10个样本。
某一种排列顺序的概率为1/10^10.
(2)比如,用0-9个数字进行组合,得到的样本就是:
0123456789, 1234567890, 2345678901......9012345678等等。
每个串都是一个事件,一共有10*9*8*7*6*5*4*3*2*1个样本 = 10!个样本。
某一种组合的概率为:1/10!.
因此,古典概率的本质是用自然数的排列或组合标识样本事件(需要把实际生活或实验翻译成自然数),用自然数统计样本的总数。这几是古典概率!!!!
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123724932
以上是关于[机器学习与scikit-learn-36]:算法-分类-一元离散随机变量=>样本空间=>古典概率模型(事件自然数等概率均匀分布)的主要内容,如果未能解决你的问题,请参考以下文章