[机器学习与scikit-learn-35]：算法-分类-从另一个角度理解概率论-2：图示常见一元随机变量的概率（密度）函数
Posted 文火冰糖的硅基工坊
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[机器学习与scikit-learn-35]：算法-分类-从另一个角度理解概率论-2：图示常见一元随机变量的概率（密度）函数相关的知识，希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123618654
目录
第2章 常见一元离散型随机变量概率分布（用概率（密度）函数表达）
第3章 常见一元连续型随机变量概率分布（用概率（密度）函数表达）
第1章 概率函数、概率分布函数、概率密度函数
1.1 引言
我们常听说概率分布函数，如二项分布、(n重伯努利实验)、伽玛分布、均匀分布、指数分布、泊松分布、正态分布。这里涉及到XXX分布，如最常见的正态分布。
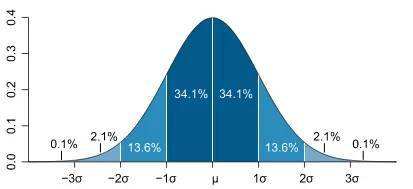
这里涉及到三部分的内容：
（1）xxx是什么含义？代表不同形态的概率分布，正态分布只是其中一种。
（2）分布是什么含义？这个词最容易误解，概率分布的定义与XXX分布给出的函数不太一致，本文首先要阐述这个概念的差异。
（3）函数是什么含义？代表了随机变量的取值与其取值出现的可能性（概率）之间的关系。这里涉及到的函数，都属于随机函数，也称为概率函数。
1.2 概率函数/概率密度函数
概率函数/概率密度可以看成是相同的定义，它是一种自变量为随机变量，因变量是概率的随机函数。
f = f（x） =》 p= P（x）
- X：随机变量
- P：某种特定分布的概率分布函数，也称为随机函数, 如正态分布，均匀分布、指数分布等。
- p：概率
x在某个点处的概率可以表示为：
p= P（x=A） = Px=A = P(A).
1.3 概率分布函数的定义
概率分布函数是概率论的基本概念之一。在实际问题中，常常要研究一个随机变量ξ取值小于某一数值x的概率，这概率是x的函数，称这种函数为随机变量ξ的分布函数，简称分布函数，记作F(x)，即F(x)=P(ξ<x) (-∞<x<+∞)，由它并可以决定随机变量落入任何范围内的概率。
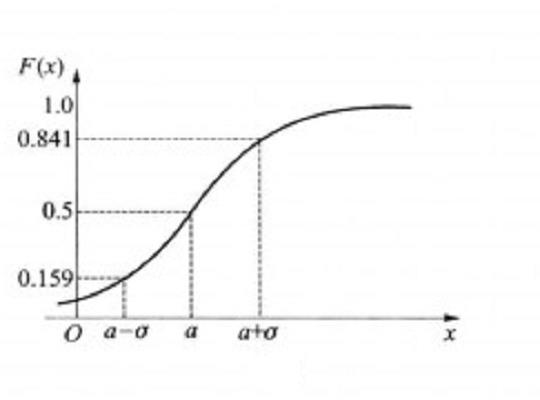
简单的讲，在概率论中，概率分布函数是概率密度函数或概率函数在（X<x区间）内的概率函数的积分。
1.4 正态密度函数与正态分布函数的区别
下面这张图充分展现了正态（密度）函数与 正态分布函数的区别。
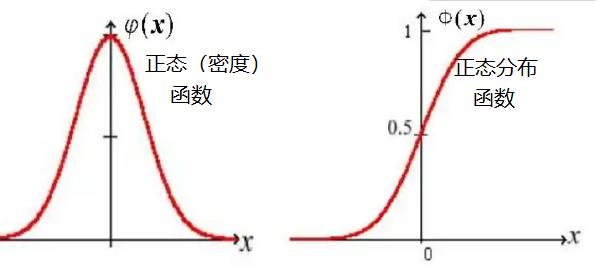
左图：正态密度函数，反应了在不同X点处的概率值，是随机函数，用f（x）表示。
右图：正态分布函数，反应了在不同的X点处的概率积分值，是单调递增函数，用F（x）表示。
在实际过程中，xxx分布函数用得比较少，大多数时候给出的XXX分布的函数，是指xxx概率分布函数。比如，给出的正态分布的函数：
该函数的几何图形：
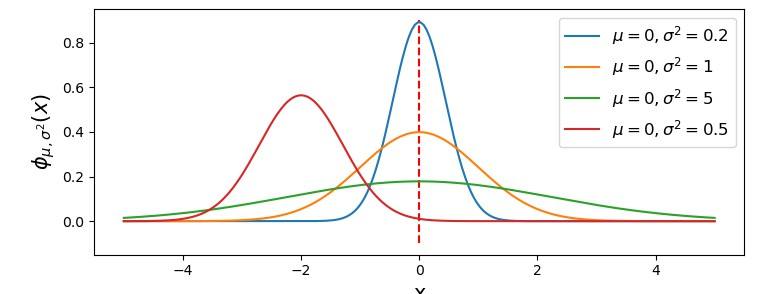
我们常说的正态分布，无论是给出的图像，还是给出的数学函数的，实际上给出的是：正态密度函数或正态函数f(x), 而不是正态分布函数F（x）。
因此，本文后续要探讨的XXX分布给出的图像或函数，都是指XXX概率密度函数或xxx概率函数，而不是XXX概率分布函数。
第2章 常见一元离散型随机变量概率分布（用概率（密度）函数表达）
2.1 说明
（1）一元是指只有一个随机变量X
（2）离散型概率函数也可以通过离散随机变量的特性来分类
2.2 伯努利（随机）分布
随机变量只有两种可能的取值：1-成功和0-失败，随机变量符合这样特征的概率函数，称为伯努利（随机）分布。
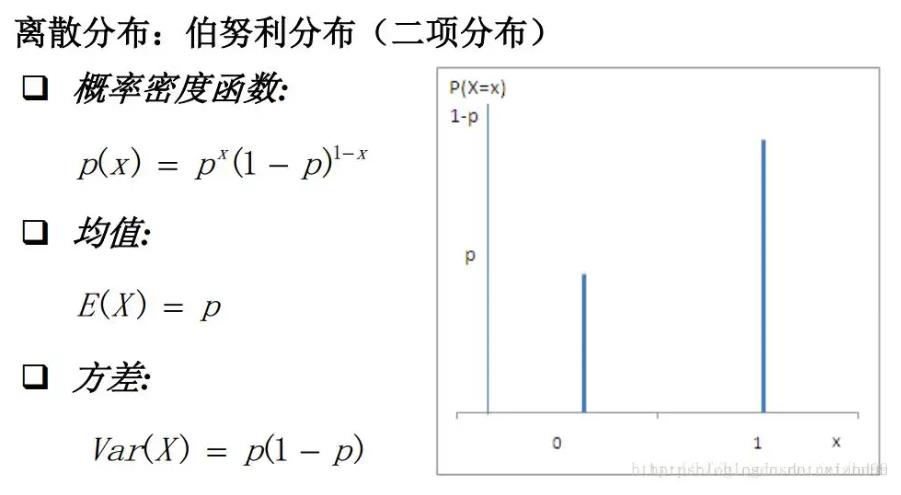
在上图中，x=0时的概率为p，则取1的概率为1-p.
Px=0 = p
Px=1 = 1-p
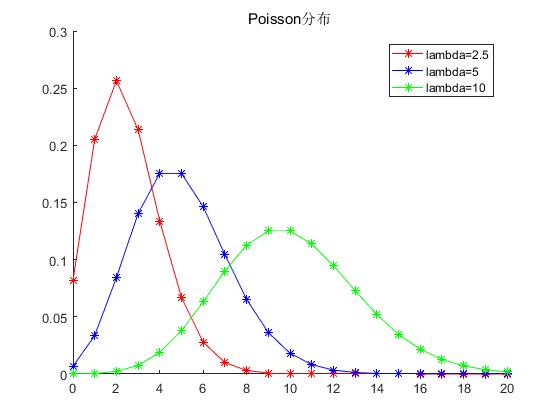
2.3 泊松分布
Poisson分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。
第3章 常见一元连续型随机变量概率分布（用概率（密度）函数表达）
3.1 说明
（1）一元是指只有一个随机变量X
（2）连续型概率函数也可以通过连续型随机变量的特性来分类。
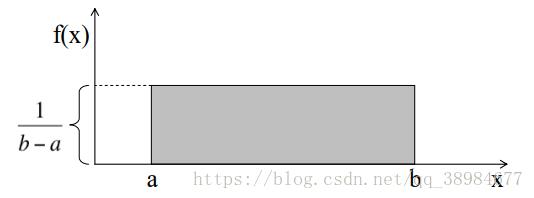
3.2 均匀分布
均匀分布所有可能结果的n个数的发生概率是相等的，均匀分布变量X的概率密度函数为：
3.3 指数函数
连续随机变量X的概率密度为
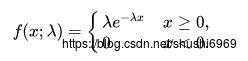
其中λ>0,为常数，则称X服从参数为λ的指数分布。
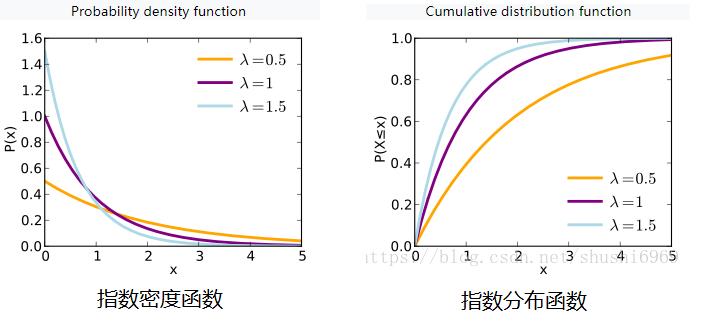
在概率论和统计学中，指数分布是一种连续概率分布。
指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。
随着时间t的变化，其函数值按照指数的方式减少特征的场合，就可以利用指数函数。
3.4 正态分布
正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution）
正态的英文的nommal，为啥是normal呢？ 这说明，这个函数的分布形态反应的是大自然的普遍规律，是非常常态性的分布规律。正因为如此，正态分布应用及其广泛。
自然界、人类社会、心理和教育中大量现象均按正态形式分布，例如能力的高低，学生成绩的好坏等都属于正态分布。它随随机变量的平均数、标准差的大小与单位不同而有不同的分布形态。
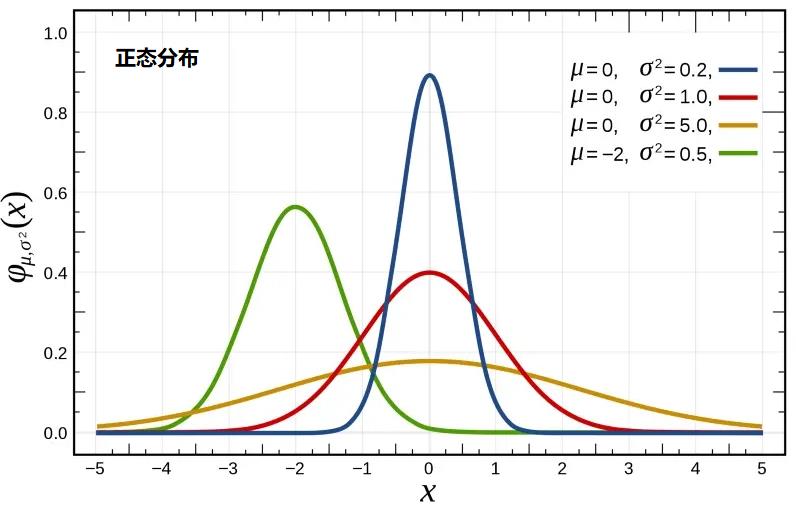
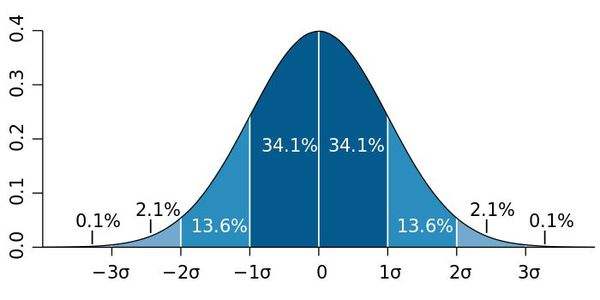
3.5 标准正态分布
标准正态分布是正态分布的一种，其平均数和标准差都是固定的，平均数为u=0，标准差为1的正态分布函数。
作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客
本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123618654
以上是关于[机器学习与scikit-learn-35]：算法-分类-从另一个角度理解概率论-2：图示常见一元随机变量的概率（密度）函数的主要内容，如果未能解决你的问题，请参考以下文章
机器学习资料《分布式机器学习算法理论与实践》+《白话机器学习算法》+《Python机器学习基础教程》