[机器学习与scikit-learn-23]:算法-聚类-KMeans算法的工作原理
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-23]:算法-聚类-KMeans算法的工作原理相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:
目录
第1章 KMeans概述
作为聚类算法的典型代表,KMeans可以说是最简单的聚类算法没有之一,那它是怎么完成聚类的呢?
1.1 什么是簇与质心
(1)什么是族
KMeans算法将一组N个样本的特征矩阵X(实际上是空间向量点)划分为K个无交集的簇。
直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。
簇就是聚类的结果表现。

(2)什么是“质心”
簇中所有数据的均值, 通常被称为这个簇的“质心”(centroids)。
在一个二维平面中,一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值,质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

(3)KMeans的目标
在KMeans算法中,簇的个数K是一个超参数,需要我们人为输入来确定。
KMeans的核心任务就是根据我们设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。
1.2 质心的计算过程
(1)确定初始质心
随机抽取K个样本作为最初的质心,这时候的质心其实是不准确的,这没有关系,后续的迭代过程会修正。
K的数量根据样本的分布特征认为指定的,如下图形,就可以规定4个质心。

(2)循环迭代,更新质心
- 样本点归类
将每个样本点分配到离他们最近的质心,生成K个簇。
何为最近? 即计算剩余每个点,计算每个点到当前K个质心的距离,即每个样本点多有K个距离,然后选择距离最小的质心,最为该点的归类对象。当所有的点归类完成后,一次迭代就完成了。
- 更新K个质心的位置
对于每个簇,计算所有被分到该簇的样本点的平均值作为新的质心
(3)迭代结束条件
当质心的位置不再发生变化,迭代停止,聚类完成。
那什么情况下,质心的位置会不再变化呢?
当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了。
这个过程在可以由下图来显示,我们规定,将数据分为4簇(K=4),其中白色X代表质心的位置:

在数据集下多次迭代(iteration),就会有如下图,经过6次迭代,基本是质心的位置就确定了。

第2章 聚合指标
2.1 距离和度量方法
质心是族内所有点的算术均值,是一个向量点。
距离是族内所有样本点到质心的距离和
而距离的衡量方法有多种:

(1)欧几里得距离:几何距离
欧几里得距离,则一个簇中所有样本点到质心的距离的平方和为:

其中,m为一个簇中样本的个数,j是每个样本的编号。这个公式被称为簇内平方和(cluster Sum of Square),又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和(Total Cluster Sum ofSquare),又叫做total inertia。
Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。
因此KMeans追求的是,求解能够让Inertia最小化的质心。实际上,在质心不断变化不断迭代的过程中,总体平方和是越来越小的。如此,K-Means的求解过程,就变成了一个最优化问题,即什么时候平方和最小的问题。
可以数学证明:当整体平方和最小的时候,质心就不再发生变化了,反之亦然。
2.2 聚合的意义
类算法聚出的类有什么含义呢?这些类有什么样的性质?
我们认为,被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的,当聚类完毕之后,我们就要分别去研究每个簇中的样本都有什么样的性质,从而根据业务需求制定不同的商业或者科技策略。这个听上去和我们在上周的评分卡案例中讲解的“分箱”概念有些类似,即我们分箱的目的是希望,一个箱内的人有着相似的信用风险,而不同箱的人的信用风险差异巨大,以此来区别不同信用度的人,因此我们追求“组内差异小,组间差异大”。
聚类算法也是同样的目的,我们追求“簇内差异小,簇外差异大”。而这个“差异“,由样本点到其所在簇的质心的距离来衡量。对于一个簇来说,所有样本点到质心的距离之和越小,我们就认为这个簇中的样本越相似,簇内差异就越小。
2.3 Kmeans有损失函数吗?
在逻辑回归中曾有这样的结论:
损失函数本质是用来衡量模型的拟合效果的,只有有着求解参数需求的算法(并非所有算法),才会有损失函数。
Kmeans不求解什么参数,它的模型本质也没有在拟合数据,而是在对数据进行一种探索,是不断探索质心新位置的过程,而质心的位置不取决于某个模型的动态参数,而取决于预先设定的超参数和数据集自身:当每次聚类迭代后,整体的族内的内平方和最小的时候,就是族心确定的时候。
所以如果你去问大多数数据挖掘工程师,甚至是算法工程师,他们可能会告诉你说,K-Means不存在什么损失函数,Inertia更像是Kmeans的模型评估指标,而非损失函数。
类比过了Kmeans中的Inertia和逻辑回归中的损失函数的功能,我们发现它们确实非常相似。所以,从“求解模型中的某种信息,用于后续模型的使用“这样的功能来看,我们可以认为Inertia是Kmeans中的损失函数,虽然这种说法并不严谨。
对比来看,在决策树中,我们有衡量分类效果的指标准确度accuracy,准确度所对应的损失叫做泛化误差,但我们不能通过最小化泛化误差来求解某个模型中需要的信息,我们只是希望模型的效果上表现出来的泛化误差很小。
因此决策树,KNN等算法,Kmeans是绝对没有损失函数的,提到Kmeans的损失函数,只是借用其概念而已。
2.4 scikit-learn中KMeans的距离算法
Inertia默认是基于欧几里得距离的计算公式得来的。实际上,我们也可以使用其他距离,每个距
离都有自己对应的Inertia。不同距离所对应的质心选择方法和Inertia,在Kmeans中,只要使用了正确的质心和距离组合,无论使用什么样的距离,都可以达到不错的聚类效果:
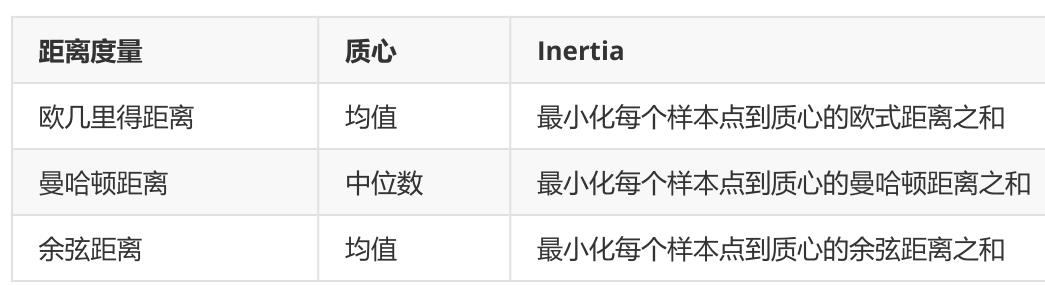
不过在sklearn当中,目前无法选择使用的其他距离,只能使用欧式距离。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:
以上是关于[机器学习与scikit-learn-23]:算法-聚类-KMeans算法的工作原理的主要内容,如果未能解决你的问题,请参考以下文章