Vitalik 系统设计中的封装复杂性和系统复杂性

Posted 2022-03-07 mutourend

1. 引言

以太坊协议设计的主要目标 之一是降低复杂性：在保证链功能和高效性能的基础上，使协议尽可能简单。

大部分以太坊协议设计于2014~2016年，协议本身并不完美，一直在致力于降低以太坊协议的复杂性。

难点之一对复杂性本身进行定义。一种方式是将其拆分为2个维度来考虑：

• 1）encapsulated complexity 封装复杂性：当系统具有子系统时，尽管子系统内部复杂，但对外暴露一个简单的接口。
• 2）systemic complexity.系统复杂性：当系统的不同部分无法干净地拆分时，各个部分之间有复杂的相互交互。

2. BLS签名 VS Schnorr签名

详细可参看博客：

• ECDSA VS Schnorr signature VS BLS signature

BLS和Schnorr是基于椭圆曲线构建的2种很流行的密码学签名机制。

BLS签名从数学上看起来很简单：

• BLS签名：$\sigma =H(m)\ast k$
• BLS验签：$e([1],\sigma )\stackrel{?}{=}e(H(m),K)$

其中$H$为hash函数，$m$为待签名message，$k$和$K$为签名者的私钥和公钥。
BLS签名看起来很简单，但是真正的复杂性隐藏在$e$函数的定义中：elliptic curve pairings。

BLS签名需要pairing椭圆曲线，而Schnorr签名只需要basic椭圆曲线即可。但是Schnorr签名的签名和验签逻辑要更复杂：

• Schnorr签名：待签名消息为$M$：

  • 从allowed set中选出随机值$k$
  • 令$r=g^k$
  • 令$e=H(r||M)$，其中$||$表示拼接，$r$以bit string表示。
  • 令$s=k-xe$
    完整的签名表示为$(s,e)$ pair。

• Schnorr验签：

  • 令$r_v=g^s{y}^e$
  • 令$e_v=H(r_v||M)$
    若$e_v=e$，则验签通过。

哪种签名更简单呢？具体取决于你所关注的点。BLS签名具有大量的技术复杂性，但是该复杂性隐藏在$e$函数的定义之下。若将$e$函数看成是黑盒，则BLS签名确实非常简单。而Schnorr签名具有更少的total complexity，但是BLS签名具有更多的pieces，可与外界进行巧妙的互动。如：

• 1）实现BLS多签（对2个秘钥$k_1,k_2$的签名进行合成）是很容易的：仅需要${\sigma }_1+{\sigma }_2$。而，Schnorr多签需要2轮交互，同时需要考虑处理Key Cancellation Attack。
• 2）Schnorr签名需要生成随机数，而BLS签名中不需要随机数。

Elliptic curve pairings是一种强大的“complexity sponge”，其内部包含了大量的封装复杂性，但是整体方案具有更少的系统复杂性。

同理，对于 KZG commitments（需要pairings），比 inner product arguments（不需要pairings），具有更复杂的内部逻辑。

3. Cryptography vs Cryptoeconomics

很多链在设计时都需要考虑 Cryptography vs Cryptoeconomics。如对于rollups 会在validity proofs（又名ZK-SNARKs）与 fraud proofs之间进行选择。

ZK-SNARKs为复杂的技术。但ZK-SNARK背后的工作原理可以一篇博客解释清楚。在ZK-SNARK中，验证某些计算需要的复杂性 比 计算本身 要复杂多倍。这也是为啥 ZK-SNARKs for the EVM 仍然在开发中，而fraud proofs for the EVM 已进入测试阶段。

• 高效实现ZK-SNARK需要 进行具有特殊优化的circuit设计 + 使用不熟悉的编程语言 等各种挑战。
• 而Fraud proofs本质更简单：若某人发起挑战，你仅需直接在链上运行相应的计算。为了效率，有时会增加binary-search机制，但是这并不会增加多少复杂性。

尽管ZK-SNARKs是复杂的，但其是封装复杂性。而相对低复杂度的fraud proofs，其是系统复杂性。

fraud proofs中的系统复杂性示例有：

• 1）需要仔细的激励工程，来避免Verifier困境。
• 2）若在共识层实现，需要为fraud proofs定义额外的交易类型，并需要考虑当有多个actors同时竞争提交fraud proof的情况。
• 3）需依赖同步网络。
• 4）支持censorship attack，也可用于commit theft。
• 5）基于fraud proofs的Rollups要求liquidity providiers支持instant withdrawals。

基于以上原因，以及密码学方案的复杂性角度来看，ZK-SNARKs具有更长期的安全性：ZK-SNARKs have are more complicated parts that some people have to think about, but they have fewer dangling caveats that everyone has to think about.

4. 其它示例

• Proof of work（Nakamoto consensus）：具有低封装复杂性，该机制非常简单易于理解，但具有更高的系统复杂性（如selfish mining attacks）。
• Hash函数：高封装复杂性，但具有非常易于理解的低系统复杂性。
• Random shuffling算法：shuffling算法可：
  • 为 内部复杂的（如Whisk），具有易于理解的枪随机性。
  • 为 内部简单的，但具有更弱的随机性，且更难于分析（高系统复杂性）。
• Miner extractable value（MEV）：很强大的协议，支持复杂的交易，但其内部非常简单，而这些复杂交易可具有高系统复杂性，以一种非常规的方式影响产块激励。
• Verkle trees：Verkle trees具有一定的封装复杂性，但其实际上确实比Merkle hash trees要更复杂一点点。但是，系统上，Verkle tree可为a key-value map提供相对clean-and-simple接口。主要的系统复杂性 “leak”在于：可能有攻击者可操纵tree，使得某特定value具有很长的branch，但是这种风险对于Verkle trees和Merkle trees都是一样的。

5. 如何来权衡封装复杂性和系统复杂性

大多数情况下选择低封装复杂性也意味着低系统复杂性。有些封装复杂性也会影响系统复杂性。

以以太坊的two-level state tree为例，其为a tree of account objects，而每个account object又具有其自己的storage tree：

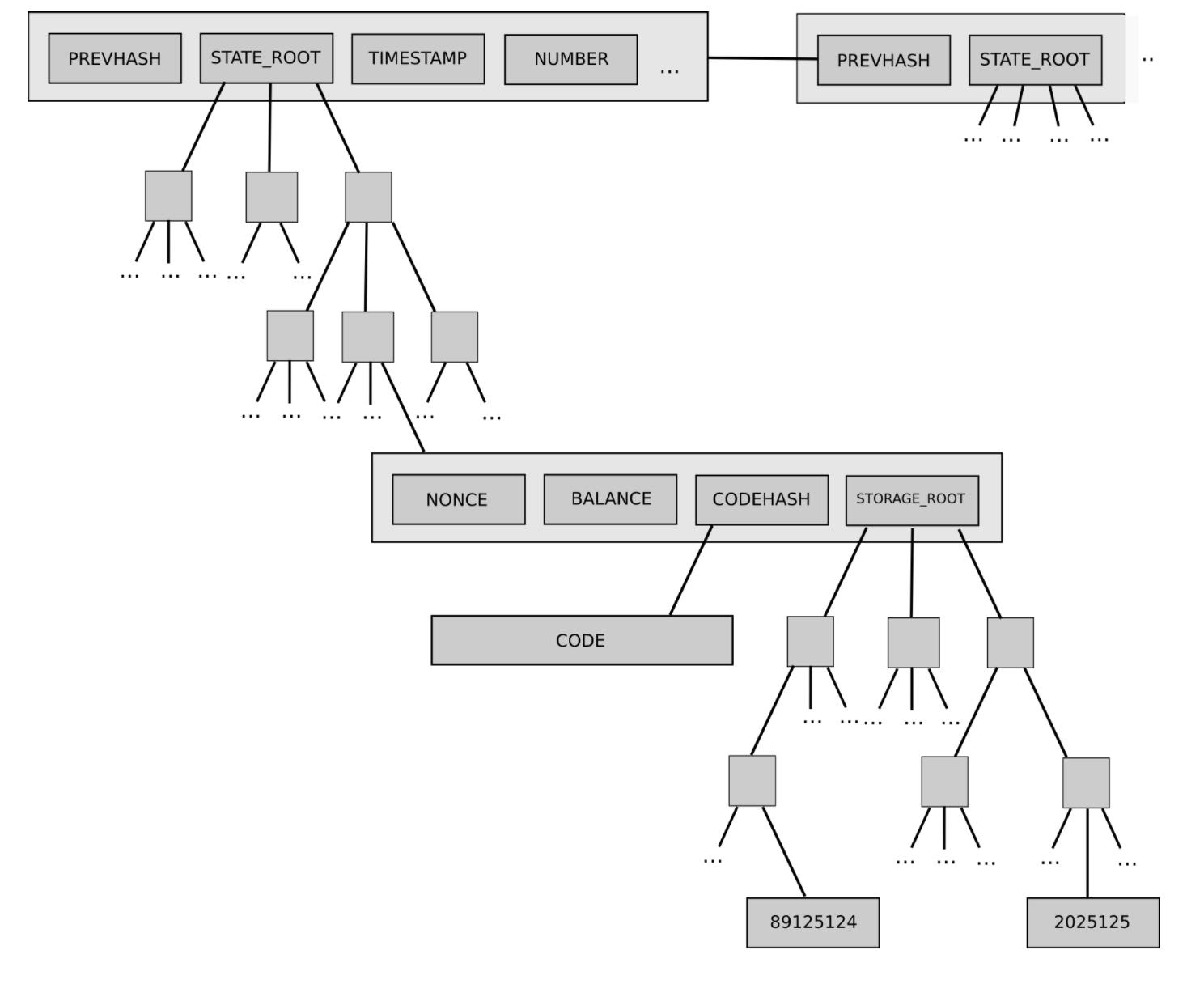
以太坊的two-level state tree结构复杂，一开始看其复杂性似乎封装得很好，协议的其它部分通过a key/value store来与该two-level state tree进行读/写交互，因此，无需关注该tree的具体结构。
但是，随后，这种封装复杂性产生了系统效应：accounts可以有任意大的storage trees，即意味着没办法可靠地期望某个特定的状态片段（例如，“所有以0x1234开头的帐户”）具有可预测的大小。从而使得将状态切分为片段更困难，使同步协议设计复杂化，并尝试distribute the storage process。
为什么封装复杂性成为了系统复杂性？因为接口改变了。
如何解决呢？当前的建议是替换为使用Verkle tree ，并对该Verkle tree进行well-balanced single-layer设计。

实际在封装复杂性和系统复杂性权衡过程中，可多实际测试平衡。

参考资料

[1] Vitalik 2022年2月博客 Encapsulated vs systemic complexity in protocol design