什么是最大公约数

Posted 2023-05-12

最普遍的介绍：

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数，a，b的最小公倍数记为[a，b]。

【拓展资料】

一、基本概念及举例说明：

1、如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系，不能单独存在。

举例：只能说16是某数的倍数，2是某数的约数，而不能孤立地说16是倍数，2是约数。

2、“倍”与“倍数”是不同的两个概念，“倍”是指两个数相除的商，它可以是整数、小数或者分数。“倍数”只是在数的整除的范围内，相对于“约数”而言的一个数字的概念，表示的是能被某一个自然数整除的数。

3、几个整数中公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数。

举例：12、16的公约数有1、2、4，其中最大的一个是4，4是12与16的最大公约数，一般记为（12，16）=4。12、15、18的最大公约数是3，记为（12，15，18）=3。

4、几个自然数公有的倍数，叫做这几个数的公倍数，其中最小的一个自然数，叫做这几个数的最小公倍数。

举例：4的倍数有4、8、12、16，……，6的倍数有6、12、18、24，……，4和6的公倍数有12、24，……，其中最小的是12，一般记为[4，6]=12。12、15、18的最小公倍数是180。记为[12，15，18]=180。若干个互质数的最小公倍数为它们的乘积的绝对值。

二、最大公约数的常见求法

1、质因数分解法

思路：把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数。

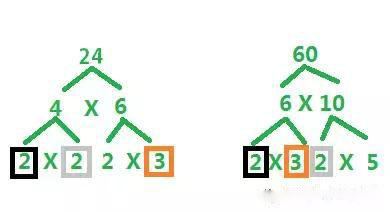
举例：假设我们求24和60的最大公约数。

第一步：分解24和60。

24=2X2X2X3

60=2X3X2X5

第二步：24和60的最大公约数=24和60共有的公因子相乘，即2X2X3=12。

2、短除法

思路：短除法求最大公约数，先用这几个数的公约数连续去除，一直除到所有的商互质为止，然后把所有的除数连乘起来，所得的积就是这几个数的最大公约数。

短除法的本质就是质因数分解法，只是将质因数分解用短除符号来进行。

举例：

12的因数有：1、2、3、4、6、12。

18的因数有：1、2、3、6、9、18。

12与18的公因数有：1、2、3、6。

12与18的最大公因数是6。

3、更相减损法

思路：

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

举例：

用更相减损术求98与63的最大公约数。

由于63不是偶数，把98和63以大数减小数，并辗转相减：

98-63=35

63-35=28

35-28=7

28-7=21

21-7=14

14-7=7

所以，98和63的最大公约数等于7。

4、辗转相除法

用较小数除较大数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。

举例：

求（319，377）：

∵ 319÷377=0（余319）

∴（319，377）=（377，319）；

∵ 377÷319=1（余58）

∴（377，319）=（319，58）；

∵ 319÷58=5（余29）

∴ （319，58）=（58，29）；

∵ 58÷29=2（余0）

∴ （58，29）= 29；

∴ （319，377）=29。

参考技术A 最大公约数

最大公约数（greatest common divisor，简写为gcd；或highest common factor，简写为hcf)，指某几个整数共有因子中最大的一个。

例如，12和30的公约数有：1、2、3、6，其中6就是12和30的最大公约数。

两个整数的最大公约数主要有两种寻找方法：

* 两数各分解质因子，然后取出同样有的项乘起来
* 辗转相除法（扩展版）

和最小公倍数（lcm）的关系：gcd(a, b)×lcm(a, b) = ab

两个整数的最大公因子可用于计算两数的最小公倍数，或分数化简成最简分数。

两个整数的最大公因子和最小公倍数中存在分配律：

* gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))
* lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))

在坐标里，将点(0, 0)和(a, b)连起来，通过整数坐标的点的数目（除了(0, 0)一点之外）就是gcd(a, b)。本回答被提问者采纳 参考技术B 最大公约数也称为最大公因数、最大公因子，指两个或多个整数共有约数中最大的一个。如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。约数和倍数都表示一个整数与另一个整数的关系，不能单独存在。例如只能说16是某数的倍数，2是某数的约数，而不能孤立地说16是倍数，2是约数a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数，a，b的最小公倍数记为[a，b]。 参考技术C 就是两个或两个以上的自然数拥有的公约数中最大的一个！例如20的约数有：1、2、4、5、10、20；30的约数有：1、2、3、5、6、10、15、30。此时这两个数的最大公约数就是10，因为它们的公约数有1、2、5、10这几个，而10最大嘛！ 参考技术D 同时被两个或两个以上的自然数整除的数中,最大的,就是最大公约数

HashMap的最大容量为什么是2的30次方？

今天看HashMap的底层实现，发现HashMap的最大容量规定为：

1. // 最大容量（必须是2的幂且小于2的30次方，传入容量过大将被这个值替换）

2. static final int MAXIMUM_CAPACITY = 1 << 30;

当看到 1<<30 时，对“<<” 有点模糊，当了解“<<”的用法之后，又有一个问题；

int类型不是4个字节共32位吗，为什么不是 1<<31呢？

首先介绍下等号右边数字及字符的含义:

1、"<<"为左移运算符，1表示十进制中的“1”，30表示十进制数字1转化为二进制后向左移动30位。在数值上等同于2的30次幂。

2、为什么是2的30次幂?

以一个字节为例：1<<2 = 4

0000 0001(十进制1)

向左移动两位之后变成

0000 0100（十进制4）

可见 1<<30 等同于十进制中2的30次幂。

回到题目，为什么会是2的30次幂，而不是2的31次幂呢？

首先：JAVA规定了该static final 类型的静态变量为int类型，至于为什么不是byte、long等类型，原因是由于考虑到HashMap的性能问题而作的折中处理！

由于int类型限制了该变量的长度为4个字节共32个二进制位，按理说可以向左移动31位即2的31次幂。但是事实上由于二进制数字中最高的一位也就是最左边的一位是符号位，用来表示正负之分（0为正，1为负），所以只能向左移动30位，而不能移动到处在最高位的符号位！

--------------------- 本文来自 爱码僧 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/qq_33666602/article/details/80139620?utm_source=copy