leetcode算法231.2 的幂

Posted 2022-03-03 学无止境小奇

👏👏👏

哈喽！大家好，我是【学无止境小奇】，一位热爱分享各种技术的博主！😍😍😍

⭐【学无止境小奇】的创作宗旨：每一条命令都亲自执行过，每一行代码都实际运行过，每一种方法都真实实践过，每一篇文章都良心制作过。✊✊✊

⭐【学无止境小奇】的博客中所有涉及命令、代码的地方，除了提供图片供大家参考，另外会在图片下方提供一份纯文本格式的命令或者代码方便大家粘贴复制直接执行命令或者运行代码。🤝🤝🤝

⭐如果你对技术有着浓厚的兴趣，欢迎关注【学无止境小奇】，欢迎大家和我一起交流。😘😘😘

❤️❤️❤️感谢各位朋友接下来的阅读❤️❤️❤️

文章目录

• 一、leetcode算法
• • 1、2 的幂
  • • 1.1、题目
    • 1.2、思路
    • 1.3、答案

一、leetcode算法

1、2 的幂

1.1、题目

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

示例 1：

输入：n = 1
输出：true
解释：20 = 1
示例 2：

输入：n = 16
输出：true
解释：24 = 16
示例 3：

输入：n = 3
输出：false
示例 4：

输入：n = 4
输出：true
示例 5：

输入：n = 5
输出：false

1.2、思路

思路一：此题我们可以运用二进制来进行计算，2的幂次方转换为二进制只有1个1，其余的全部为0，我们可以用n & （n-1）来判断是不是等于0，因为如果是二进制则n为100这种格式，而n-1为11这种格式，两个向&，&是两个都为1的时候为1，其余的都为0，所以这样计算就可以判断是否是2的幂次方了。

1.3、答案

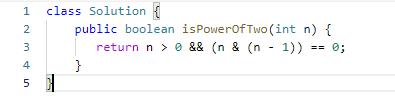
class Solution 
    public boolean isPowerOfTwo(int n) 
       return n > 0 && (n & (n - 1)) == 0;
    

复杂度分析

时间复杂度：O(1)。

空间复杂度：O(1)。