LeetCode 688. 骑士在棋盘上的概率 / 1791. 找出星型图的中心节点 / 969. 煎饼排序（冒泡排序）

Posted 2022-03-01 Zephyr丶J

688. 骑士在棋盘上的概率

2022.2.1 每日一题

题目描述

在一个 n x n 的国际象棋棋盘上，一个骑士从单元格 (row, column) 开始，并尝试进行 k 次移动。行和列是 从 0 开始 的，所以左上单元格是 (0,0) ，右下单元格是 (n - 1, n - 1) 。

象棋骑士有8种可能的走法，如下图所示。每次移动在基本方向上是两个单元格，然后在正交方向上是一个单元格。

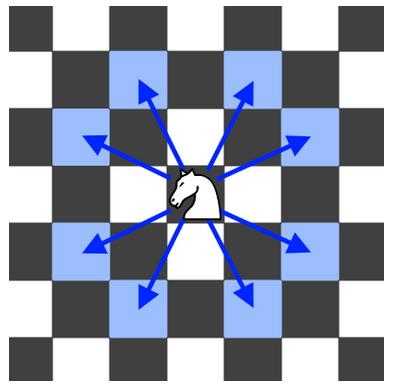
每次骑士要移动时，它都会随机从8种可能的移动中选择一种(即使棋子会离开棋盘)，然后移动到那里。

骑士继续移动，直到它走了 k 步或离开了棋盘。

返回 骑士在棋盘停止移动后仍留在棋盘上的概率 。

示例 1：

输入: n = 3, k = 2, row = 0, column = 0
输出: 0.0625
解释: 有两步(到(1,2)，(2,1))可以让骑士留在棋盘上。
在每一个位置上，也有两种移动可以让骑士留在棋盘上。
骑士留在棋盘上的总概率是0.0625。

示例 2：

输入: n = 1, k = 0, row = 0, column = 0
输出: 1.00000

提示:

1 <= n <= 25
0 <= k <= 100
0 <= row, column <= n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/knight-probability-in-chessboard
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

记忆化搜索
需要注意的是数据范围，必须用double才可以通过

class Solution 
    int n;
    int[][] dir = 1,2, -1,2, 1,-2, -1,-2, 2,1, 2,-1, -2,1, -2,-1;
    int res = 0;
    double[][][] graph;
    public double knightProbability(int n, int k, int row, int column) 
        //首先要读懂题，移动要棋盘外就不能移动了
        //看第一个示例，这个概率就是2 * 2 / 8 * 8 = 0.0625
        //在所有移动的64种情况中，有4种是可以留在棋盘上的，
        //这就给了我们一个思路
        //总共的情况就是8的k次方，而几种情况可以留在棋盘上，
        //可以遍历棋盘上的每一个点，统计每个点有几种情况是可以留在棋盘上的
        //然后从出发点开始统计
        
        //会超时，得加个记忆化
        this.n = n;
        graph = new double[n][n][k + 1];
        double temp = dfs(row, column, k);
        //System.out.println(temp);
        return (double)temp / Math.pow(8, k);
    

    public double dfs(int x, int y, int step)
        if(step == 0)
            return 1;
        if(step <= 0)
            return 0;
        if(graph[x][y][step] != 0)
            return graph[x][y][step];
        for(int[] d : dir)
            int nx = x + d[0];
            int ny = y + d[1];
            if(nx < 0 || ny < 0 || nx >= n || ny >= n)
                continue;
            graph[x][y][step] += dfs(nx, ny, step - 1);
        
        return graph[x][y][step];
    

或者写成动态规划

class Solution 
    int[][] dir = 1,2, -1,2, 1,-2, -1,-2, 2,1, 2,-1, -2,1, -2,-1;
    public double knightProbability(int n, int k, int row, int column) 
        //动态规划
        //dp[i][j][k] 表示在i,j点且剩余步数为k的时候，最后留在棋盘上的概率

        double[][][] dp = new double[n][n][k + 1];
        for(int step = 0; step <= k; step++)
            for(int i = 0; i < n; i++)
                for(int j = 0; j < n; j++)
                    if(step == 0)
                        dp[i][j][0] = 1;
                    else
                        for(int[] d : dir)
                            int x = i + d[0];
                            int y = j + d[1];
                            if(x < 0 || y < 0 || x >= n || y >= n)
                                continue;
                            dp[i][j][step] += dp[x][y][step - 1] / 8;
                        
                    
                
            
        
        return dp[row][column][k];
    

1791. 找出星型图的中心节点

2022.2.18 每日一题

题目描述

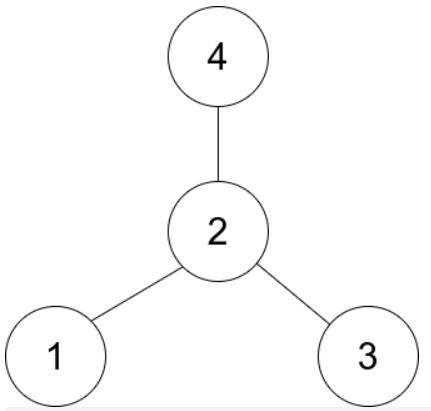
有一个无向的 星型 图，由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点，并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。

给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。

示例 1：

输入：edges = [[1,2],[2,3],[4,2]]
输出：2
解释：如上图所示，节点 2 与其他每个节点都相连，所以节点 2 是中心节点。

示例 2：

输入：edges = [[1,2],[5,1],[1,3],[1,4]]
输出：1

提示：

3 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
题目数据给出的 edges 表示一个有效的星型图

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-center-of-star-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

class Solution 
    public int findCenter(int[][] edges) 
        //因为是星型图，边数都是固定的，每个点只有与中心节点的一条边
        //所以直接看哪个点连接了两条边就行了

        //两个边中肯定有一个数字是相同的，所以找到这个相同的数字就可以了
        if(edges[0][0] == edges[1][0] || edges[0][0] == edges[1][1])
            return edges[0][0];
        else
            return edges[0][1];
    

969. 煎饼排序

2022.2.19 每日一题

题目描述

给你一个整数数组 arr ，请使用 煎饼翻转 完成对数组的排序。

一次煎饼翻转的执行过程如下：

选择一个整数 k ，1 <= k <= arr.length
反转子数组 arr[0...k-1]（下标从 0 开始）

例如，arr = [3,2,1,4] ，选择 k = 3 进行一次煎饼翻转，反转子数组 [3,2,1] ，得到 arr = [1,2,3,4] 。

以数组形式返回能使 arr 有序的煎饼翻转操作所对应的 k 值序列。任何将数组排序且翻转次数在 10 * arr.length 范围内的有效答案都将被判断为正确。

示例 1：

输入：[3,2,4,1]
输出：[4,2,4,3]
解释：
我们执行 4 次煎饼翻转，k 值分别为 4，2，4，和 3。
初始状态 arr = [3, 2, 4, 1]
第一次翻转后（k = 4）：arr = [1, 4, 2, 3]
第二次翻转后（k = 2）：arr = [4, 1, 2, 3]
第三次翻转后（k = 4）：arr = [3, 2, 1, 4]
第四次翻转后（k = 3）：arr = [1, 2, 3, 4]，此时已完成排序。

示例 2：

输入：[1,2,3]
输出：[]
解释：
输入已经排序，因此不需要翻转任何内容。
请注意，其他可能的答案，如 [3，3] ，也将被判断为正确。

提示：

1 <= arr.length <= 100
1 <= arr[i] <= arr.length
arr 中的所有整数互不相同（即，arr 是从 1 到 arr.length 整数的一个排列）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/pancake-sorting
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

class Solution 
    public List<Integer> pancakeSort(int[] arr) 
        //怎么翻转呢，把当前最大的数换到第一位，然后翻转，就到了后面
        //例如第一个例子 3 2 4 1
        //翻转前三个 4 2 3 1，然后翻转前四个 1 3 2 4
        //然后翻转前两个 3 1 2 4，翻转前三个 2 1 3 4
        //然后翻转前两个，方法可行

        int l = arr.length;
        int max = l;
        int idx = l - 1;
        List<Integer> list = new ArrayList<>();
        while(idx > 0)
            int temp = 0;
            for(int i = 0; i <= idx; i++)
                if(arr[i] == max)
                    temp = i;
                
            
            if(temp != idx)
                reverse(arr, temp, idx);
                list.add(temp + 1);
                list.add(idx + 1);
            
            max--;
            idx--;
        
        return list;
    
    public void reverse(int[] arr, int temp, int idx)
        int left = 0;
        int right = temp;
        while(left < right)
            int t = arr[left];
            arr[left++] = arr[right];
            arr[right--] = t;
        
        left = 0;
        right = idx;
        while(left < right)
            int t = arr[left];
            arr[left++] = arr[right];
            arr[right--] = t;