蓝桥杯十大常见天阶功法——虫之呼吸.贰之型.二分
Posted 杨枝
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯十大常见天阶功法——虫之呼吸.贰之型.二分相关的知识,希望对你有一定的参考价值。
友友们好(^-^)🌹🌹🌹,我是杨枝,一枚在算法领域迈步的呆萌的博主呀~
目前还是一只纯纯的菜汪🐶。 典型的又菜又爱闹那种👀,做不好很多事,说不好很多话,写题还总不Ac😅,还在努力还在前进👣。
因为了,你们对我来说都是是独一无二的呀💓。在点开这篇文章的那一刻,我相信,我们之间相互需要彼此啦🌹🌹
时刻谨记:认真写算法,用心去分享。不负算法,不误卿。 感谢相遇(^㉨^)。
蓝桥杯的十种呼吸法是笔者结合自己的学习筛选出来的十个知识点。本着像看漫画一样了解算法原理。当日后自己确实遇到相关的习题了,可以再回头结合着我的题解报告来加深理解喔。
🔔八仙过海,智斗二分
小伙伴们对忍姐姐那把独特的日轮刀有没有印象了,感觉喃,舞起来好轻巧,看着好潇洒

但是忍姐姐的结局好容易爆泪点呀😭😭无限城中就这种牺牲了😭😭😭
害,得回归正题啦~
到蝴蝶屋中开始修习咱们今天要学的呼吸之法 —— 二分啦
💓据说只有10%的程序员可以写对二分
二分的基础用法是在单调序列或单调函数中进行查找。因此当问题具有单调性的时候,就一定可以通过二分把求解转换为判定。说通俗一点了,可理解为判断出答案在这个单调区间的位置
(根据复杂度理论,进行判定的难度小于进行求解)。
| 进一步,我们还可以扩展到通过三分法解决单峰函数的极值以及相关的问题。 |
| 二分难点在于对细节的处理: |
对于整数域上的二分,需要注意终止边界、左右区间取舍时的开闭情况,避免漏掉答案或造成死循环;
对于实数域的二分,需要注意精度问题。
🌟整数集合上的二分
使用二分法的前提是保证最终答案处于闭区间 [ l , r ] [l,r] [l,r]之内,循环以 l = r l = r l=r结束,每次二分的中间值 m i d mid mid会归属于左半段与右半段二者之一。
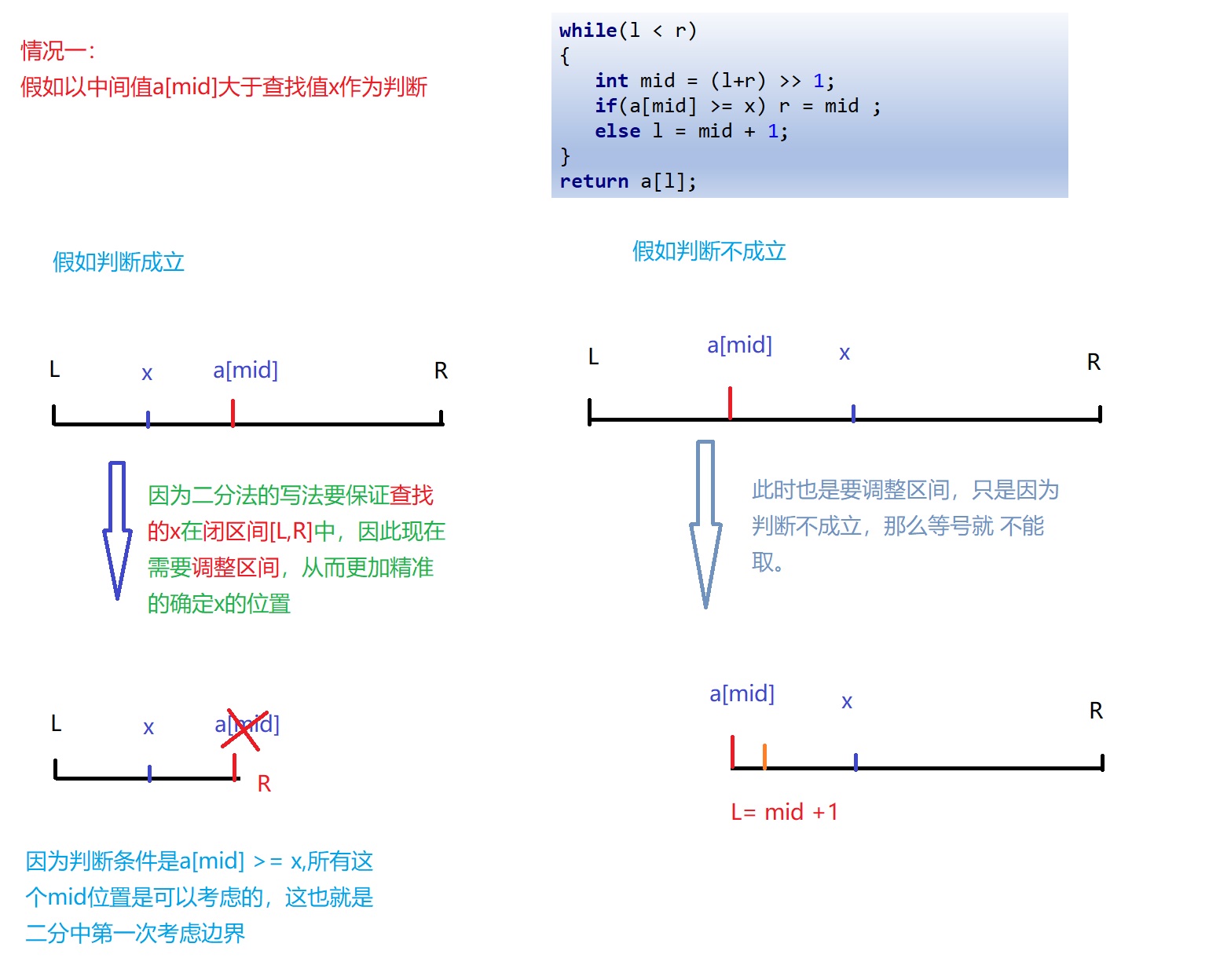
情况一:在单调递增序列 a a a中查找大于等于x的数最小的一个位置。
while(l < r)
int mid = (l+r) >> 1;
if(a[mid] >= x) r = mid ;
else l = mid + 1;
return a[l];
情况一用图片演示的效果如下:
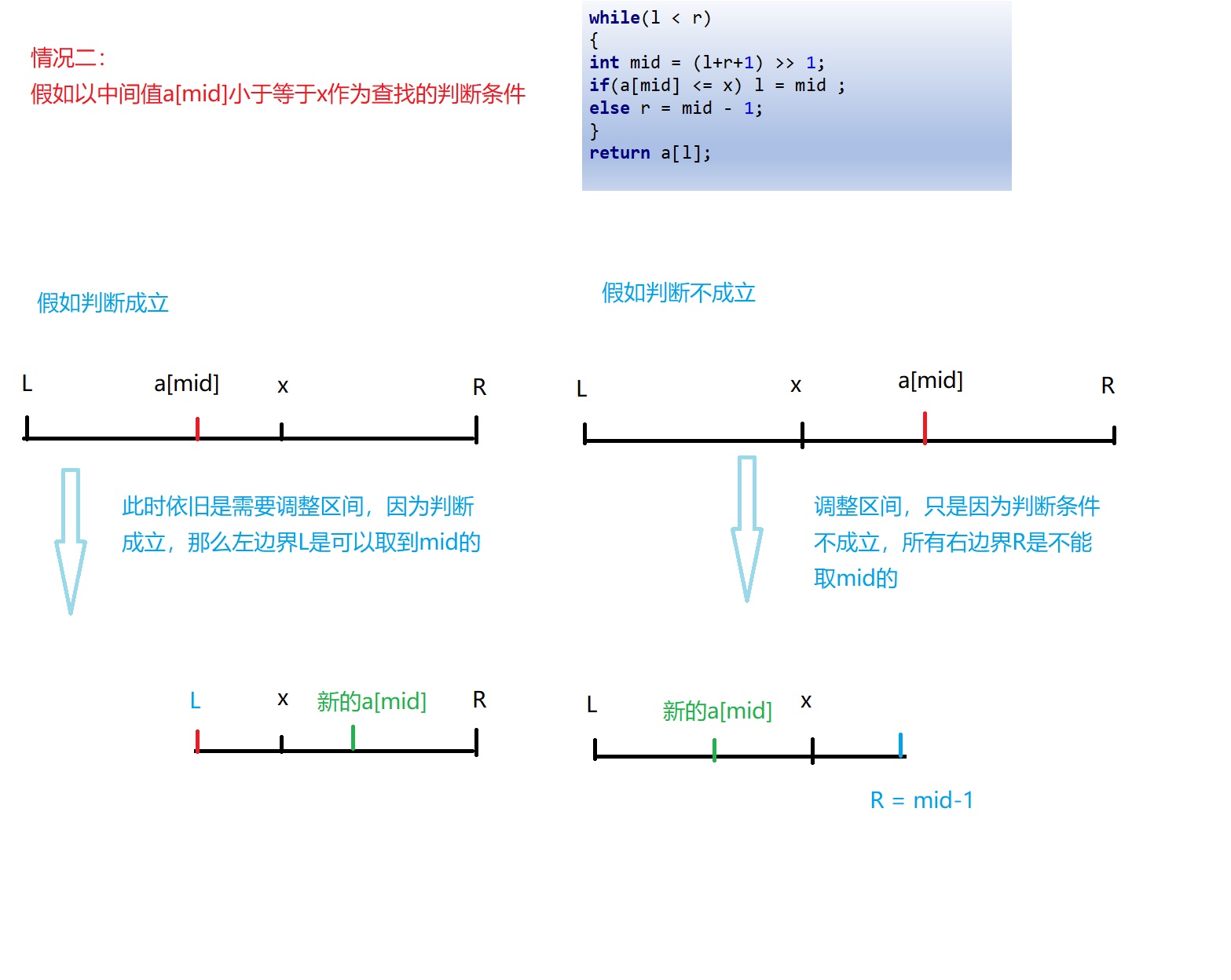
情况二:在单调递增序列a中查找小于等于x的数中最大的一个位置
while(l < r)
int mid = (l+r+1) >> 1;
if(a[mid] <= x) l = mid ;
else r = mid - 1;
return a[l];
对于情况二用图片演示效果如下:
| 如同上面两段代码所示,这种二分写法可能会有两种形式: |
1、范围缩小时, r = m i d r=mid r=mid, l = m i d + 1 l=mid+1 l=mid+1,取中间值时, m i d = ( l + r ) > > 1 mid = (l+r)>>1 mid=(l+r)>>1
2、范围缩小时, l = m i d l=mid l=mid, r = m i d − 1 r=mid-1 r=mid−1,取中间值时, m i d = ( l + r + 1 ) > > 1 mid = (l+r+1)>>1 mid=(l+r+1)>>1
注意第二段的写法,倘若第二段也是采用 m i d = ( l + r ) > > 1 mid = (l+r)>>1 mid=(l+r)>>1,那么当 r − l = 1 r-l=1 r−l=1时,即 r = l + 1 r = l+1 r=l+1,那么就会出现:
m i d = ( r + l ) > > 1 mid = (r+l)>>1 mid=(r+l)>>1 = ( l + 1 + l ) > > 1 (l+1+l)>>1 (l+1+l)>>1 = l l l。
若接下来进入 l = m i d l=mid l=mid的分支,可行的区间并没有缩小,会造成死循环。
若进入 r = m i d − 1 r = mid-1 r=mid−1的分支,会造成 l > r l>r l>r,循环结束。
因此,对两个形式采用的配套的
m
i
d
mid
mid 取法是必要也必须遵守的。

注意我们在二分中使用的是
右移运算:
>
>
1
>>1
>>1,而不是整数除法
/
2
/2
/2。两者大体是差不多的,只是有细微的区别。
| 右移运算是向下取整,而整数除法是向零取整,在二分值域包含负数时,整数除法是不能正常工作的。 |
🌟实数域上的二分
在实数域上的二分较为简单,确定好所需的精度 e p s eps eps
以 l + e p s < r l+eps<r l+eps<r 为循环条件,每次根据在 m i d mid mid 上的判断的成立与否,选择 r = m i d r=mid r=mid 或者是 l = m i d l=mid l=mid。一般需要保留 k k k 位小数的时候,则取 e p s = 1 0 − ( k + 2 ) eps = 10^-(k+2) eps=10−(k+2)
//倘若题目要求保留三位小数
while(l + 1e-5 < r)
double mid = (l+r) / 2;//在算法题里,建议多用double,float有时候会因为精度问题导致结果有细微偏差
if(判断条件) r = mid;
else l = mid;
有时候精度不容易确定或者表示,就干脆可以采用循环固定次数的二分方法,也是一种相当不错的策略,这种方式得到的结果的精度往往比设置
e
p
s
eps
eps 的更高。

for(int i = 0; i < 100;i++)
double mid = (l+r) /2;
if(判断条件) r = mid;
else l = mid;
小伙伴们现在应该有种模糊的感觉, g e t get get二分法的 精髓了,咱们着手看一点习题,切实的体会一下怎么把二分这套功法打出去吧
💓趁热打铁,开始练习
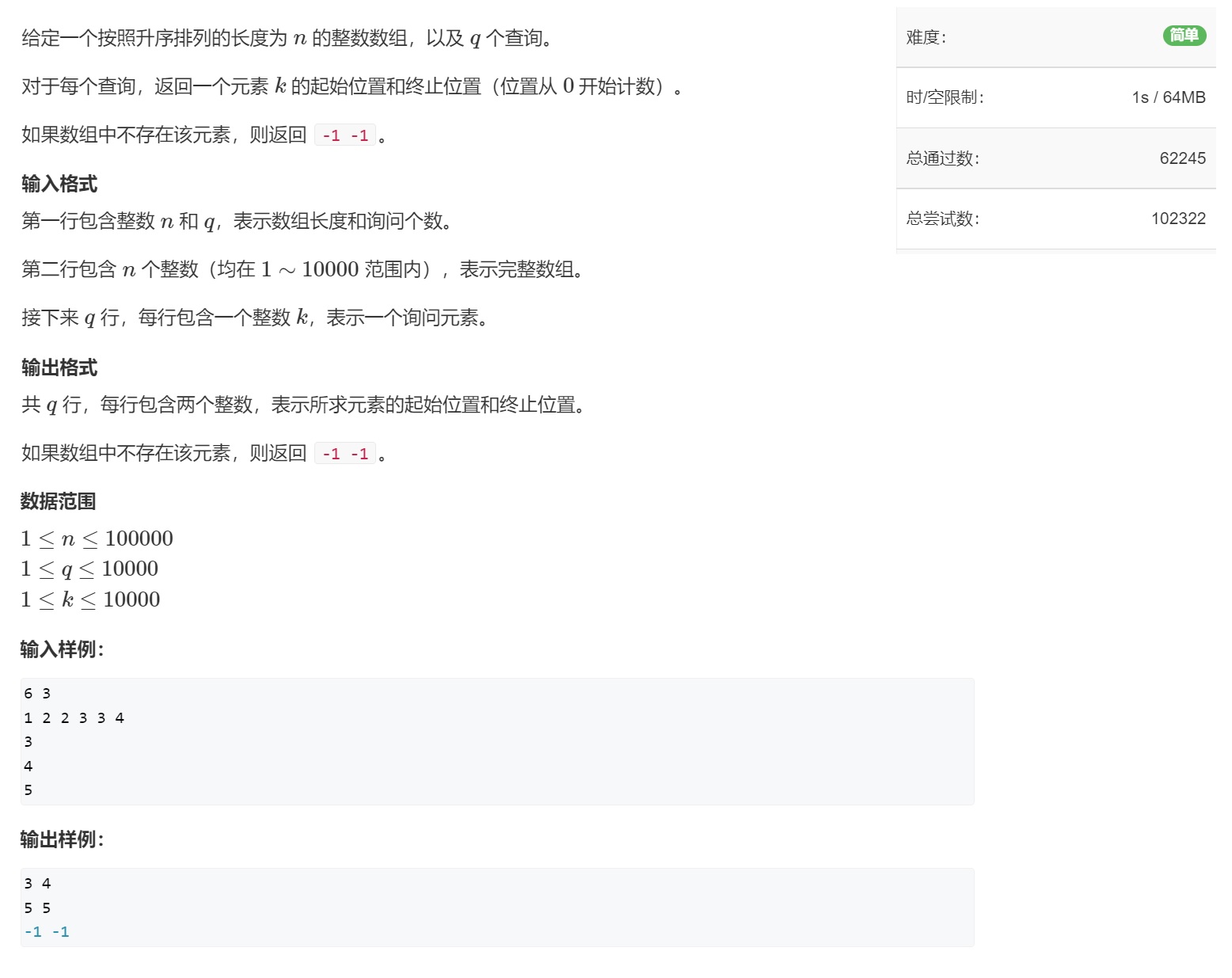
🌟例1、数的范围
🌱题目描述
🌴解题报告
| 题目想要咱们确定查找的数字的起始位置。想实现这个,就需要对二分的两种情况再理解。 |

对于情况一,在 i f ( a [ m i d ] > = x ) if(a[mid] >= x) if(a[mid]>=x)的条件下成立,那么这个查找值 x x x是在中点的左边,那就可以理解为确定当前区间的左边界
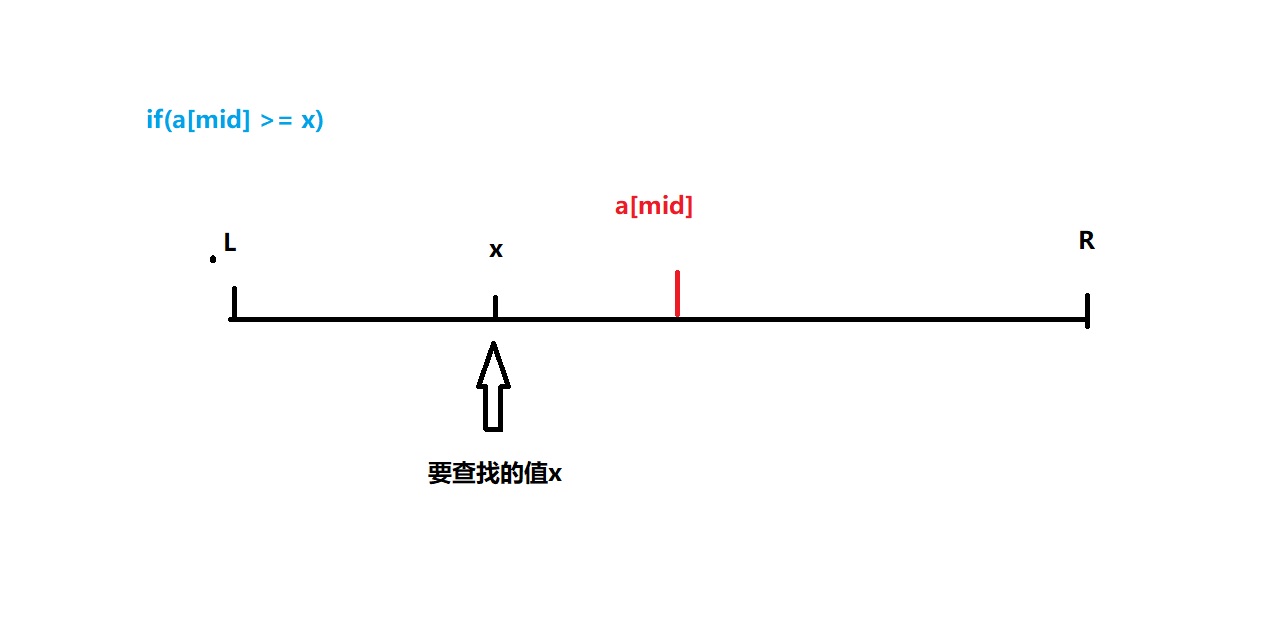
同理,对情况二进行同样的理解,情况二就可以理解为确定右边界。
那么解决这道题就很轻松啦,依次将两种情况使用上就好,注意不要将顺序弄反喔~
🌵参考代码(C++版本)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010 ;
int q[N];
int n,m;
int main()
scanf("%d %d",&n,&m);
//录入n个信息
for(int i= 0; i < n;i++) scanf("%d",&q[i]);
//m个询问
for(int i = 0; i < m;i++)
int x;
scanf("%d",&x);
//通过作图+理论分析,其实还是不恼火的
//先确定左端点
int l = 0, r = n-1;
while(l < r)
int mid = l + r >> 1;
//把这个二分出来的mid和x做比较
if(q[mid] >= x) r = mid;
else l = mid +1;
if(q[l] == x)
cout << l <<' ';
r = n-1;
//确定右端点
while(l < r)
int mid = l+r+1 >> 1;//这里按照之前的理解来分析的话,直接就裸写 l+r >> 1。再通过后面代码分析要不要补上1
if(q[mid] <= x) l = mid;
else r = mid -1;
cout << r <<endl;
else cout << "-1 -1" << endl;
return 0;
成功斩杀第一个小怪兽~,进攻下一个

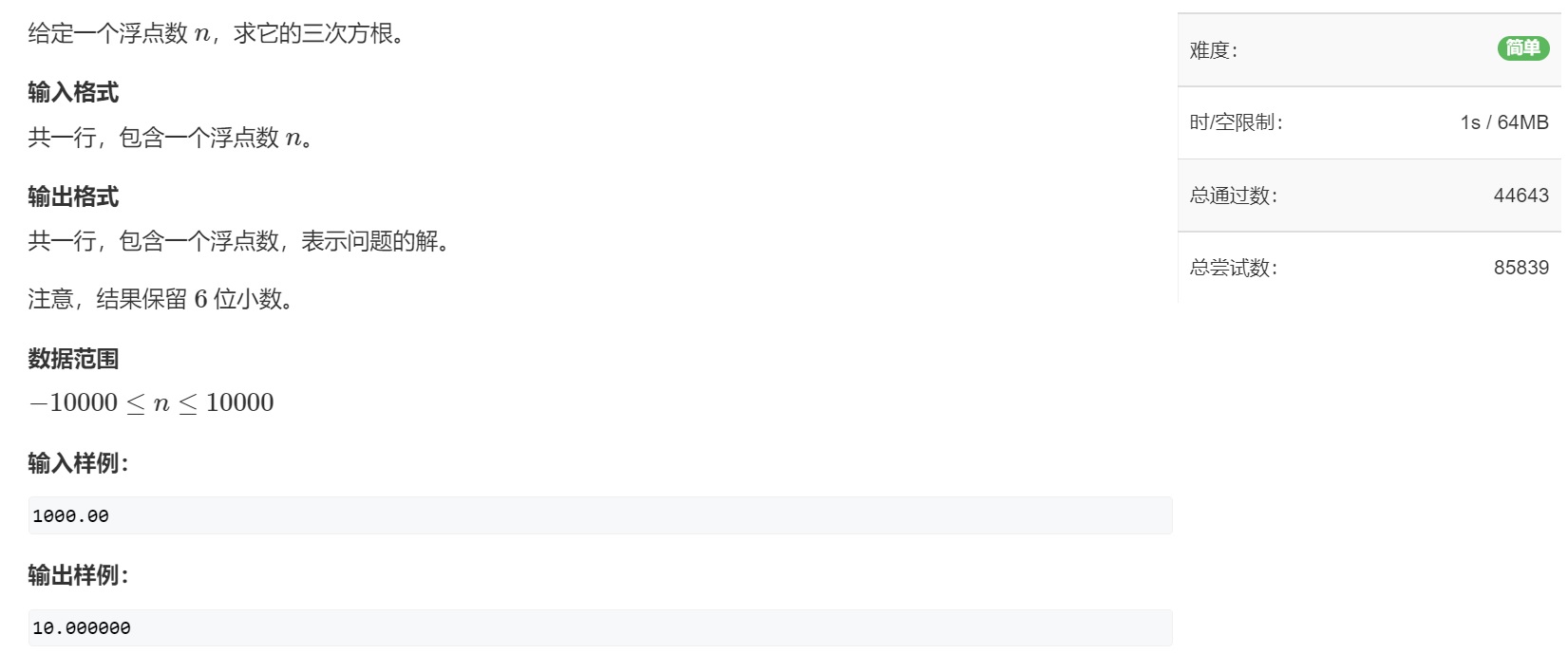
🌟例2、数的三次方根
🌱题目描述
🌴解题报告
题目给咱的的是一个浮点数,也就是属于实数域的二分。那咱们只需要指定一个判断条件,然后持续二分到精度 s p s sps sps = 10-8的程度再停止。
因为让我们求一个数的三次方根是多少,那么判断条件就可以定为:
i
f
(
m
i
d
∗
m
i
d
∗
m
i
d
>
=
x
)
if(mid * mid * mid >= x)
if(mid∗mid∗mid>=x)
🌵参考代码(C++版本)
#include <cstdio>
int main()
double x;
scanf("%lf",&x);
double l = -10000,r =10000;
while(r-l >= 1e-8)
double mid = (l+r) / 2;
if(mid*mid*mid >= x) r =mid;
else l = mid;
printf("%.6lf",l);
return 0;
完美解决

🌟例3、0到n-1中缺失的数字
🌱题目描述
🌴解题报告
这道题目给定的是递增数组,假设数组中第一个缺失的数是
x
x
x。
那么数组中下标和该下标存储的数的实际情况如下:
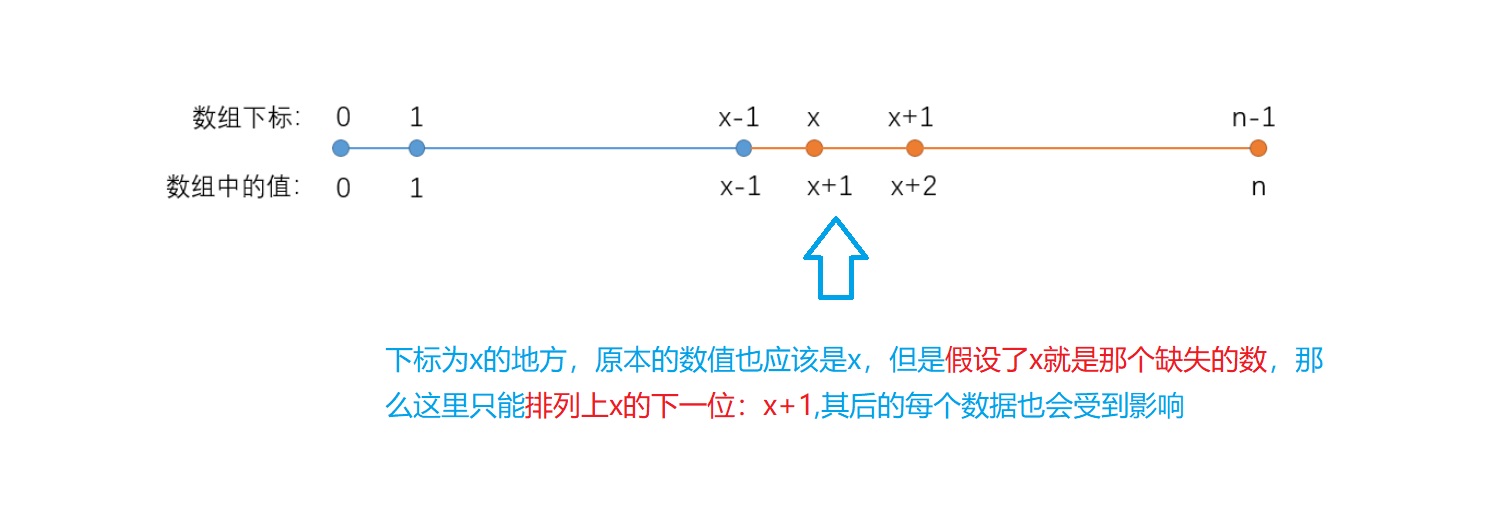
可以观察到:
可以看出,数组左边蓝色部分都满足nums[i] == i;
数组右边橙色部分都不满足nums[i] == i。
因此我们可以将是否满足nums[i] == i作为确定二分的分界点
x
x
x 的判断条件

另外要注意特殊情况:当所有数都满足nums[i] == i时,表示缺失的是
n
n
n
至于时间复杂度:
二分的迭代只会执行
O
(
l
o
g
n
)
O(logn)
O(logn) 次,那么时间复杂度
O
(
l
o
g
n
)
O(logn)
O(logn)。在时间上,完全没有问题。
🌵参考代码(C++版本)
class Solution
public:
int getMissingNumber(vector<int>& nums)
if(nums.empty()) return 0;
//二分查找
int l = 0 , r = nums.size()-1;
while(l < r)
int mid = (l+r) >> 1;
//如果二分出来的所有中点值mid,不等于对应的数据值,就继续二分查找
if(nums[mid] != mid) r = mid;
else l = mid+1;
//返回结果
if(nums[r] == r ) r++;
return r;
;
快乐Ac

🌟例4、试题 算法训练 找数2
🌱题目描述
🌴解题报告
读完题目之后,能了解到这道题是想让我们查找一个数的位置:
倘若在一串数据中查找到这个数字了,那么输出位置(注意位置是从1开始数的); 倘若没有查到这个数字,确定这个输入数据应该插入的位置。
对于查找的需求,可以使用二分来高效完成。
使用情况一和情况二都可以,注意边界。
| 对于确定插入的位置,我的思路比较暴力,是直接逐一枚举同时比较出与输入数据相差最小的数。当找到以后,这个差值最小且差值大于零的数,它后面一位就是合适的位置。 |

结合着样例,具体落实一下我刚才说的话吧,只听描述很空洞的,笔者我自己也不喜欢很空洞的东西。
样例输入
10
23 34 56 78 99 123 143 155 167 178
128
样例输出
7
比如这个样例,输入数据128和123之间的差值为5,是差值最小的正整数。123的位置是6,它后面一位就是7。
🌵参考代码(C++版本)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1010;
int q[N];
int n,mid;
int main()
int x;
int ans = 0x3f3f3f3f;
int pos = 0;
scanf("%d",&n);
//录入数据
for(int i =0; i < n;i++) scanf("%d",&q[i]);
scanf("%d",&x);
//开始二分
int l = 0, r = n-1;
while(l < r)
mid = (l + r) >> 1;
if(x <= q[mid]) r = mid;
else l = mid +1;
//二分到了,输出位置
if(x == q[l]) printf("%d",l+1);
else //没有二分到要查找的数,把插入进去
for(int i = 0; i < n;i++)
//一个小优化同时也是处理比最后一个数据还大的情况
if(x > q[n-1])
pos = n;
break;
else
if(ans > 0 && x- q[i] < ans)
ans = x-q[i];
pos = i;//记录位置
//输出位置
printf("%d",pos+1);
return 0;
从上面几个小例题中,应该逐渐体会到了,二分在查找领域里面是占了一席天地的。因为它的时间复杂度是 O ( l o g n ) O(logn) O(logn)。
就比如上海到杭州的某处电话线断了,其间有30万根电线杆,逐一枚举的话,就是30万次。
使用二分法去查找的话,大概只需用20次的样子。效率相当可观。

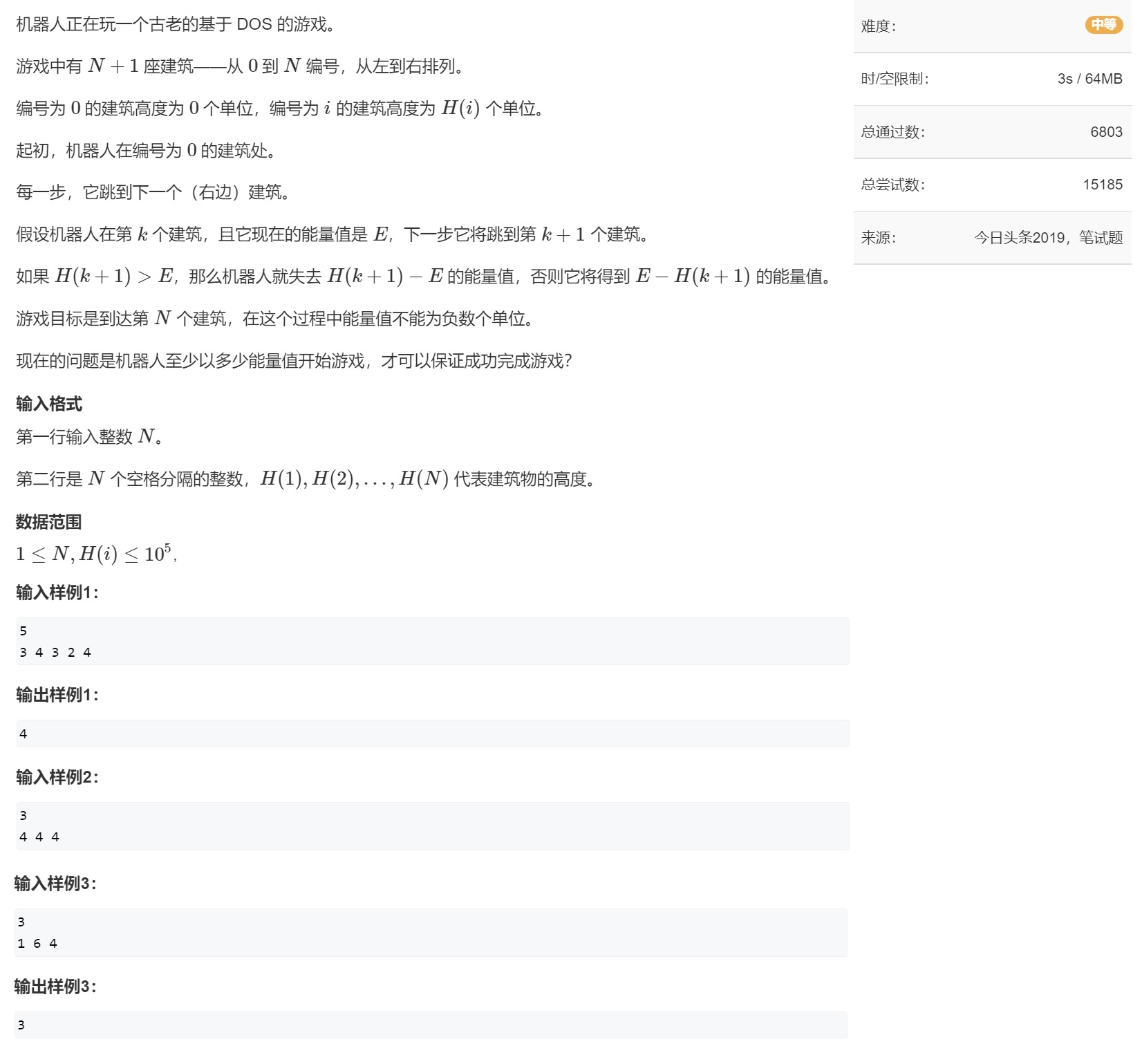
🌟例5、今日头条2019 机器人跳跃问题
🌱题目描述
🌴解题报告
一、从数据范围定算法
题目的数据范围是1到十万,根据我在水之呼吸.壹之型.递归中罗列出的表单,是可以选择二分的。比起其他算法,二分实现相对更容易,那咱们就按照二分的思路解了。

题目在输出格式中说明了要输出整数,那么这道题是隶属于整数二分

二、题目分析以上是关于蓝桥杯十大常见天阶功法——虫之呼吸.贰之型.二分的主要内容,如果未能解决你的问题,请参考以下文章