Python 大白从零开始 OpenCV 学习课-8. 频率域图像滤波（上）

Posted 2022-02-22 小白YouCans

欢迎关注 『OpenCV 例程200篇 100 篇』 系列，持续更新中
欢迎关注 『Python小白的OpenCV学习课』 系列，持续更新中

---

Python 大白从零开始 OpenCV 学习课-8. 频率域图像滤波（上）

本系列面向 Python 小白，从零开始实战解说 OpenCV 项目实战。
图像滤波是在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制，是常用的图像预处理操作。
频率域图像处理先将图像进行傅里叶变换，然后在变换域进行处理，最后进行傅里叶反变换转换回空间域。
频率域滤波是滤波器传递函数与输入图像的傅里叶变换的对应像素相乘。频率域中的滤波概念更加直观，滤波器设计也更容易。使用快速傅里叶变换算法，比空间卷积运算速度快很多。
本文提供上述各种算法的完整例程和运行结果，并通过一个应用案例示范综合使用多种图像增强方法。

---

1. 傅里叶变换

滤波通常是指对图像中特定频率的分量进行过滤或抑制。图像滤波是在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制，是常用的图像预处理操作。

图像滤波不仅可以在空间域进行还可以在频率域进行。空间滤波是图像与各种空间滤波器（模板、核）的卷积，而空间卷积的傅里叶变换是频率域中相应变换的乘积，因此频率域滤波是频率域滤波器（传递函数）与图像的傅里叶变换相乘。

频率域图像滤波，先将图像进行傅里叶变换，然后在变换域进行处理，最后进行傅里叶反变换转换回空间域。

空间域滤波器和频率域滤波器形成一个傅里叶变换对：
$$\begin{gathered} f(x,y)\otimes h(x,y)\iff F(u,v)H(u,v) \\ f(x,y)h(x,y)\iff F(u,v)\otimes H(u,v) \end{gathered}$$
也就是说，空间域滤波器和频率域滤波器实际上是相互对应的，有些空间域滤波器在频率域通过傅里叶变换实现会更方便、更快速。例如，空间域的拉普拉斯滤波器就是频率域的高通滤波器。

1.1 傅里叶级数与傅里叶变换

傅里叶级数（Fourier series）在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。

傅里叶级数公式指出，任何周期函数都可以表示为不同频率的正弦函数和/或余弦函数的加权之和：
$$\begin{array}{rl}f(t)& =A_0+\sum _{n=1}^{\infty }{A}_{n}sin(n\omega t+{\psi }_n)\\ & =A_0+\sum _{n=1}^{\infty }[a_{n}cos(n\omega t)+b_{n}sin(n\omega t)]\end{array}$$
这个和就是傅里叶级数。

进一步地，任何非周期函数也可以表示为不同频率的正弦函数和/或余弦函数乘以加权函数的积分：
$$\begin{array}{rl}F(\omega )& ={\int }_{-\infty }^{+\infty }f(t)e^{-j\omega t}dt\\ f(t)& =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(\omega )e^{j\omega t}d\omega \end{array}$$
这个公式就是傅里叶变换（Fourier transform ）和逆变换。

*傅里叶变换存在的充分条件是：f(t) 的绝对值的积分是有限的，在信号处理、图像处理领域这一条件都能满足。

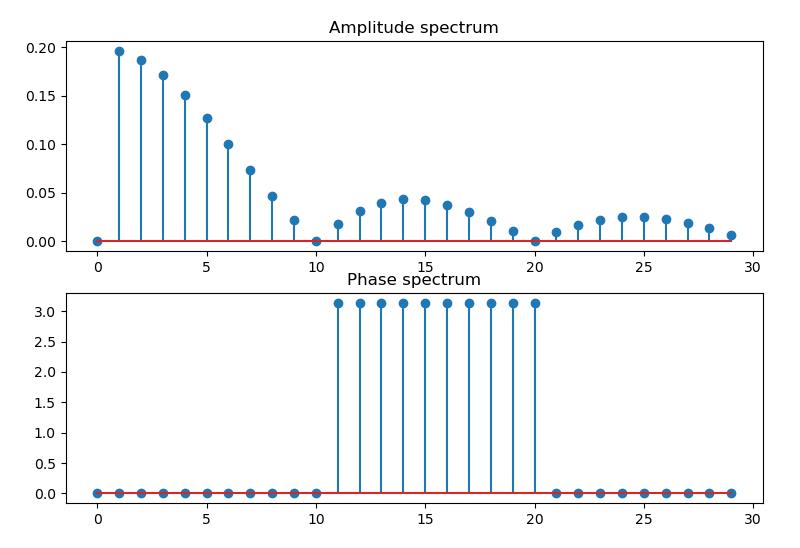
例程 8.1：连续周期信号的傅立叶级数

    # 8.1：连续周期信号的傅立叶级数
    from scipy import integrate

    nf = 30
    T = 10
    tao = 1.0
    y = 1

    k = np.arange(0, nf)
    an = np.zeros(nf)
    bn = np.zeros(nf)
    amp = np.zeros(nf)
    pha = np.zeros(nf)

    half0, err0 = integrate.quad(lambda t: y, -tao/2, tao/2)
    an[0] = 2 * half0 / T
    for n in range(1, nf):
        half1, err1 = integrate.quad(lambda t: 2*y * np.cos(2.0/T * np.pi * n * t), -tao/2, tao/2)
        an[n] = half1 / 10
        half2, err2 = integrate.quad(lambda t: 2*y * np.sin(2.0/T * np.pi * n * t), -tao/2, tao/2)
        bn[n] = half2 / 10
        amp[n] = np.sqrt(an[n]**2 + bn[n]**2)

    for i in range(0, nf):
        pha[i] = 0.0 if an[i]>=0 else np.pi

    plt.figure(figsize=(9, 6))
    plt.subplot(211), plt.title("Amplitude spectrum"), plt.stem(k, amp)
    plt.subplot(212), plt.title("Phase spectrum"), plt.stem(k, pha)
    plt.show()

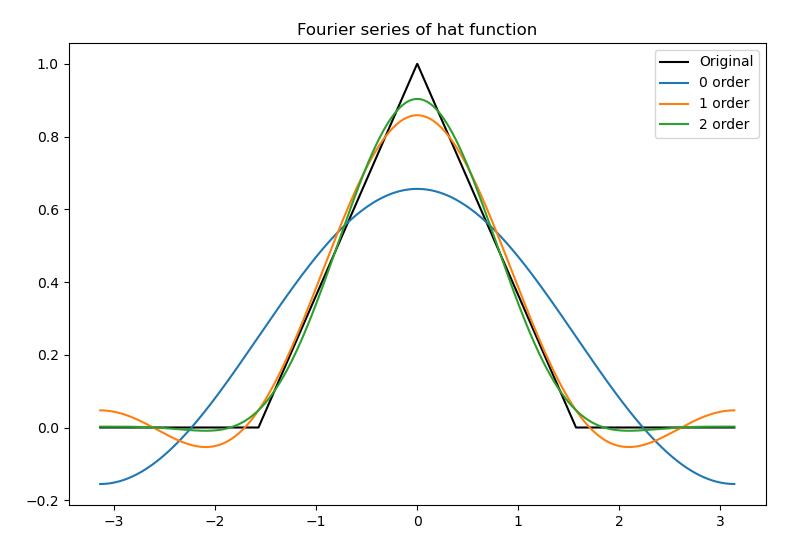
例程 8.2：连续非周期信号的傅立叶系数

    # 8.2：连续非周期信号的傅立叶系数
    dx = 0.001
    x = np.pi * np.arange(-1+dx, 1+dx, dx)
    n = len(x)
    nquart = int(np.floor(n/4))

    f = np.zeros_like(x)
    f[nquart: 2*nquart] = (4/n) * np.arange(1, nquart+1)
    f[2*nquart: 3*nquart] = np.ones(nquart) - (4/n) * np.arange(0, nquart)

    plt.figure(figsize=(9, 6))
    plt.title("Fourier series of hat function")
    plt.plot(x, f, '-', color='k',label="Original")

    # Compute Fourier series
    A0 = np.sum(f * np.ones_like(x)) * dx
    fFS = A0 / 2

    orders = 3
    A = np.zeros(orders)
    B = np.zeros(orders)
    for k in range(orders):
        A[k] = np.sum(f * np.cos(np.pi * (k+1) * x / np.pi)) * dx  # Inner product
        B[k] = np.sum(f * np.sin(np.pi * (k+1) * x / np.pi)) * dx
        fFS = fFS + A[k] * np.cos((k + 1) * np.pi * x / np.pi) + B[k] * np.sin((k + 1) * np.pi * x / np.pi)

        plt.plot(x, fFS, '-', label=" order".format(k))
        print('Line ', k, ': A = ', A[k], ' B = ', B[k], fFS.shape)

    plt.legend(loc="upper right")
    plt.show()

例程 8.3：一维连续函数的傅里叶变换（盒式函数）

以一维盒式函数为例，其傅里叶变换为：

$$\begin{array}{rl}F(\omega )& ={\int }_{-\infty }^{+\infty }f(t)e^{-j\omega t}dt\\ & ={\int }_{-\pi }^{\pi }f(t)e^{-j\omega t}dt\\ & =\frac{sin(\omega )}{\omega }\end{array}$$

    # 8.3：一维连续函数的傅里叶变换（盒式函数）
    # 盒式函数 (Box_function)
    x = np.arange(-5, 5, 0.1)
    w = 2 * np.pi
    halfW = w / 2
    y = np.where(x, x > -halfW, 0)
    y = np.where(x < halfW, y, 0)

    plt.figure(figsize=(9, 4))
    plt.subplot(131), plt.title("Box_function")
    plt.plot(x, y, '-b')

    plt.subplot(132), plt.title("Fourier transform")
    fu = np.sinc(x)
    plt.plot(x, fu, '-b')

    plt.subplot以上是关于Python 大白从零开始 OpenCV 学习课-8. 频率域图像滤波（上）的主要内容，如果未能解决你的问题，请参考以下文章
 
 Python 大白从零开始 OpenCV 学习课-1.安装与环境配置
 Python 大白从零开始 OpenCV 学习课-5. 图像的几何变换
 Python 大白从零开始 OpenCV 学习课-3.图像的创建与修改
 Python 大白从零开始 OpenCV 学习课-4.图像的叠加与混合
 Python 大白从零开始 OpenCV 学习课-6. 灰度变换与直方图处理
 Python 大白从零开始 OpenCV 项目实战 图像读取与显示