谁来解释一下用辗转相除法求最两个数的最大公约数原理

Posted 2023-05-11

辗转相除法求最大公约数原理：
设两数为a、b(a>b)，用gcd(a,b)表示a，b的最大公约数，r=a (mod b) 为a除以b的余数，k为a除以b的商，即a÷b=k.......r。辗转相除法即是要证明gcd(a,b)=gcd(b,r)。
第一步：令c=gcd(a,b)，则设a=mc，b=nc
第二步：根据前提可知r =a-kb=mc-knc=(m-kn)c
第三步：根据第二步结果可知c也是r的因数
第四步：可以断定m-kn与n互质(假设m-kn=xd，n=yd (d>1)，则m=kn+xd=kyd+xd=(ky+x)d，则a=mc=(ky+x)cd，b=nc=ycd，则a与b的一个公约数cd>c，故c非a与b的最大公约数，与前面结论矛盾)，因此c也是b与r的最大公约数。
从而可知gcd(b,r)=c，继而gcd(a,b)=gcd(b,r)。
证毕。
以上步骤的操作是建立在刚开始时r≠0的基础之上的。即m与n亦互质。 参考技术A m=7560
n=2700
r=2160
m=2700
n=2160
r=540
m=2160 n=540
r=0
所以2700和7560最大公约数是540
然后在还用540和3960求最大公约数
m=3960
n=540
r=180
m=540
n=180
r=0
所以3个数最大公约数是180

用python语言求两个数的最大公约数和最小公倍数

答：可使用辗转相除法来求最大公约数和最小公倍数，总结一句话就是除数变被除数,余数变除数,当余数为零时取对应算式的除数为最大公约数。这是实现思路，对于具体的Python代码如下所示。

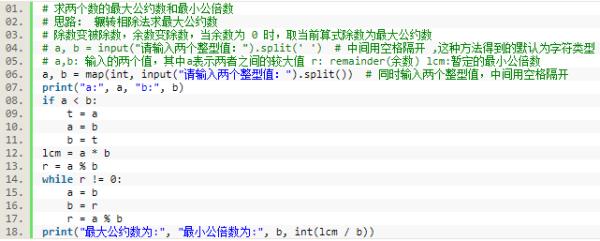
代码的具体实现中的疑难点及与注释的方式给出。

其中两次运行结果如下所示,可以求得对应的结果。

参考技术A def gcd(a,b):
if a == 0:
return b
return gcd( b%a ,a)
a = 24
b = 36
print('最大公约数是:，最小公倍数是:。'.format(gcd(a,b),a*b/gcd(a,b))) 参考技术B # 2021-05-11 Luke
while True:
try:
num1 = int(input("请输入第一个数:"))
num2 = int(input("请输入第二个数:"))

i = 2
a = []
b = []
d = []
num = [num1, num2]
num.sort()
while i <= num1:
if num1 % i == 0:
a.append(i)
i += 1
j = 2
while j <= num2:
if num2 % j == 0:
b.append(j)
j += 1
for c in a:
if c in b:
d.append(c)
d.sort(reverse=True)

if num[1] % num[0] == 0:
print(str(num1) + "和" + str(num2) + "的最小公倍数是:" + str(num[1]))
print(str(num1) + "和" + str(num2) + "的最大公约数是:" + str(d[0]))
else:
e = num1 * num2
print(str(num1) + "和" + str(num2) + "的最小公倍数是:" + str(e))
print(str(num1) + "和" + str(num2) + "的最大公约数是:" + str(d[0]))
except IndexError:
print(str(num1) + "和" + str(num2) + "没有公约数")