2020 时序分析(19) AR 模型
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2020 时序分析(19) AR 模型相关的知识,希望对你有一定的参考价值。
参考技术A 对于平稳时间的序列,可以采用 AR 和 MA 模型进行预测,他们组合起来就是 ARMA 模型。先说 AR 模型吧,所谓 AR(Autoregressive) ,翻译过来是自回归模型。下面自回归标准公式,大家只要读懂这个公式,那么应该对 AR 模型问题不大。来解释一下这个公式,这个公式如何表示自回归。首先 t 时刻 y 随机变量表示当前时刻要计算(预测)的随机变量,这里 y 是随机变量而不是值,而是一个随机变量。
首先之前一直在说平稳的时间序列,AR 模型前提条件就是要研究时间序列应该是平稳的。那么复习一下满足什么条件时间序列是平稳时间序列
前两个条件比较容易理解,而不同时刻只要间隔相同,他们的协方差值是时间间隔 k 相关,这样也就是说明时间间隔有一定关系所以才有研究价值,如果不同时刻的两两协方差是 0 也就是每一个时刻都是两两独立,也就是纯随机平稳时间序列。
c 表示一个常数,然后从 t-1 到 t-p 的过去时刻观察值,其实就是在这些时刻随机函数的一个观察值,前面系数表示该时刻值对当前 t 时刻 y 最后 epsilon 扰动项,随意是一个随机函数。无论是 AR 模型还是 MA 都有一个扰动项,
这里的 是均值为 0 方差为 1 的正态分布
我们都已经熟悉了什么是线性回归,这里以简单线性回归可以表示
其中 y hat 是预测值,x 是样本,而 b 表示截距,那么接下来扩展到多元线性回归,其中第 i 个样本 x,用上标表示 i 个样本,下标表示 i 个样本第 i 个特性。也就是样本 x 有 n 特征,也就是 tensor 维度,然后通过将这些样本特征线性组合加上一个常数项对的 y hat。这个看起来和我们时间序列是不是有点像是
所谓自回归我们认为当前时刻的随机变量和过去一段时间内每一个时刻值存在一定关系,所以将过去时刻看成自变量,当前时刻看成因变量。这里 x 的 i 特征变为了 t-1 或者 t-2 时刻的随机变量 y 的线性组合 c 有点类似截距 b。不过这里多了一个扰动项。
解 1 阶线性差分方差
其中
对差分方程进行求解,1 阶自回归模型
特征根法
有了线性差分方程可以推导序列的特征,现在时间序列建模过程就是上面过程相反过程,推导出现象差分方程。这是从差分方程用途,从数学角度解释了时间序列。这也就是给时间序列找到数学来源
TimeQuest 静态时序分析 基本概论
1. 背景
静态时序分析的前提就是设计者先提出要求,然后时序分析工具才会根据特定的时序模型进行分析,给出正确是时序报告。
进行静态时序分析,主要目的就是为了提高系统工作主频以及增加系统的稳定性。对很多数字电路设计来说,提高工作频率非常重要,因为高工作频率意味着高处理能力。通过附加约束可以控制逻辑的综合、映射、布局和布线,以减小逻辑和布线延时,从而提高工作频率。
2. 理论分析
2.1 固定参数launch edge、latch edge、Tsu、Th、Tco概念
2.1.1 launch edge
时序分析起点(launch edge):第一级寄存器数据变化的时钟边沿,也是静态时序分析的起点。
2.1.2 latch edge
时序分析终点(latch edge):数据锁存的时钟边沿,也是静态时序分析的终点。
2.1.3 Clock Setup Time (Tsu)
建立时间(Tsu):是指在时钟沿到来之前数据从不稳定到稳定所需的时间,如果建立的时间不满足要求那么数据将不能在这个时钟上升沿被稳定的打入触发器。如图3.2所示:

图3.2 建立时间图解
2.1.4 Clock Hold Time (Th)
保持时间(Th):是指数据稳定后保持的时间,如果保持时间不满足要求那么数据同样也不能被稳定的打入触发器。保持时间示意图如图3.3所示:
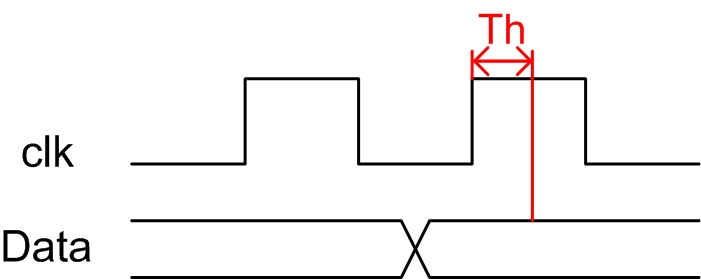
图3.3 保持时间图解
2.1.5 Clock-to-Output Delay(tco)
数据输出延时(Tco):这个时间指的是当时钟有效沿变化后,数据从输入端到输出端的最小时间间隔。
2.2 Clock skew
时钟偏斜(clock skew):是指一个时钟源到达两个不同寄存器时钟端的时间偏移,如图3.4所示:
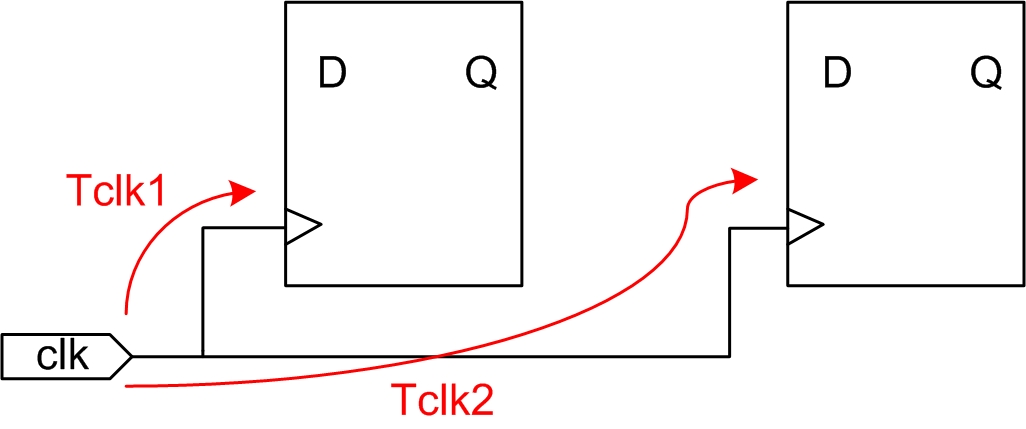
图3.4 时钟偏斜
时钟偏斜计算公式如下:
Tskew = Tclk2 - Tclk1 (公式2-1)
2.2 Data Arrival Time
数据到达时间(Data Arrival Time):输入数据在有效时钟沿后到达所需要的时间。主要分为三部分:时钟到达寄存器时间(Tclk1),寄存器输出延时(Tco)和数据传输延时(Tdata),如图3.5所示
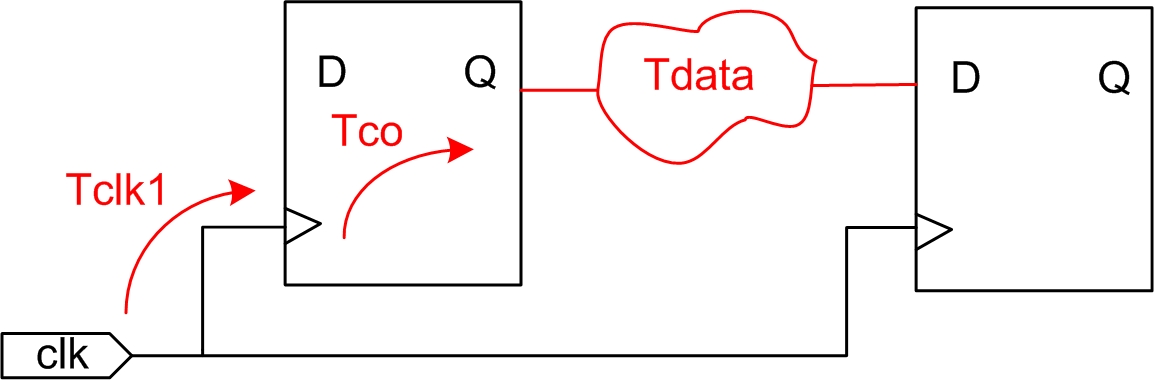
图3.5 数据到达时间
数据到达时间计算公式如下:
Data Arrival Time = Launch edge + Tclk1 +Tco + Tdata (公式2-2)
2.3 Clock Arrival Time
时钟到达时间(Clock Arrival Time):时钟从latch边沿到达锁存寄存器时钟输入端所消耗的时间为时钟到达时间,如图3.6所示
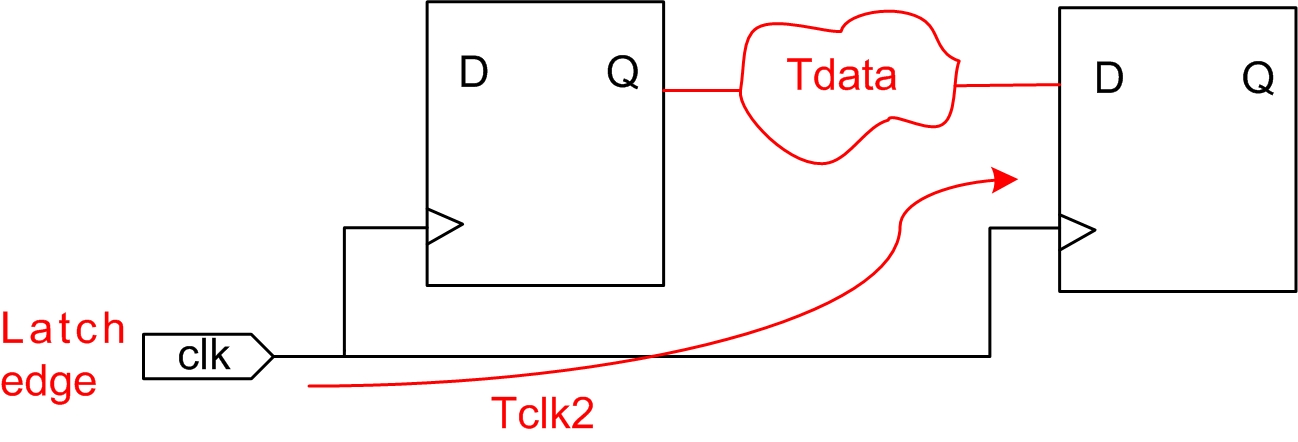
图3.6 时钟到达时间
时钟到达时间计算公式如下:
Clock Arrival Time = Lacth edge + Tclk2 (公式2-3)
2.4 Data Required Time(setup/hold)
数据需求时间(Data Required Time):在时钟锁存的建立时间和保持时间之间数据必须稳定,从源时钟起点达到这种稳定状态需要的时间即为数据需求时间。如图3.7所示:
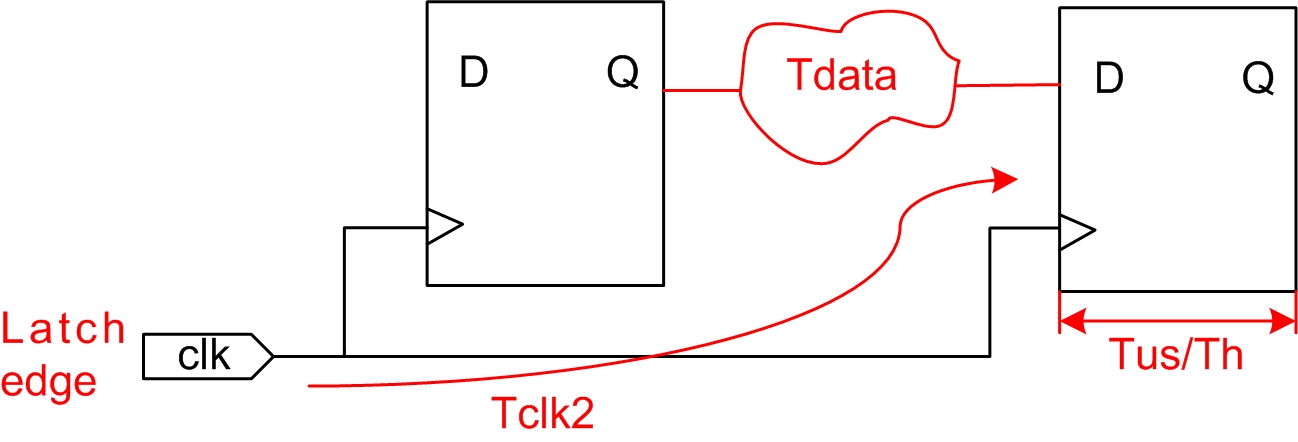
图3.7 数据需求时间
(建立)数据需求时间计算公式如下:
Data Required Time = Clock Arrival Time - Tsu (公式2-4)
(保持)数据需求时间计算公式如下:
Data Required Time = Clock Arrival Time + Th (公式2-5)
2.5 Setup slack
建立时间余量(setup slack):当数据需求时间大于数据到达时间时,就说时间有余量,Slack是表示设计是否满足时序的一个称谓。
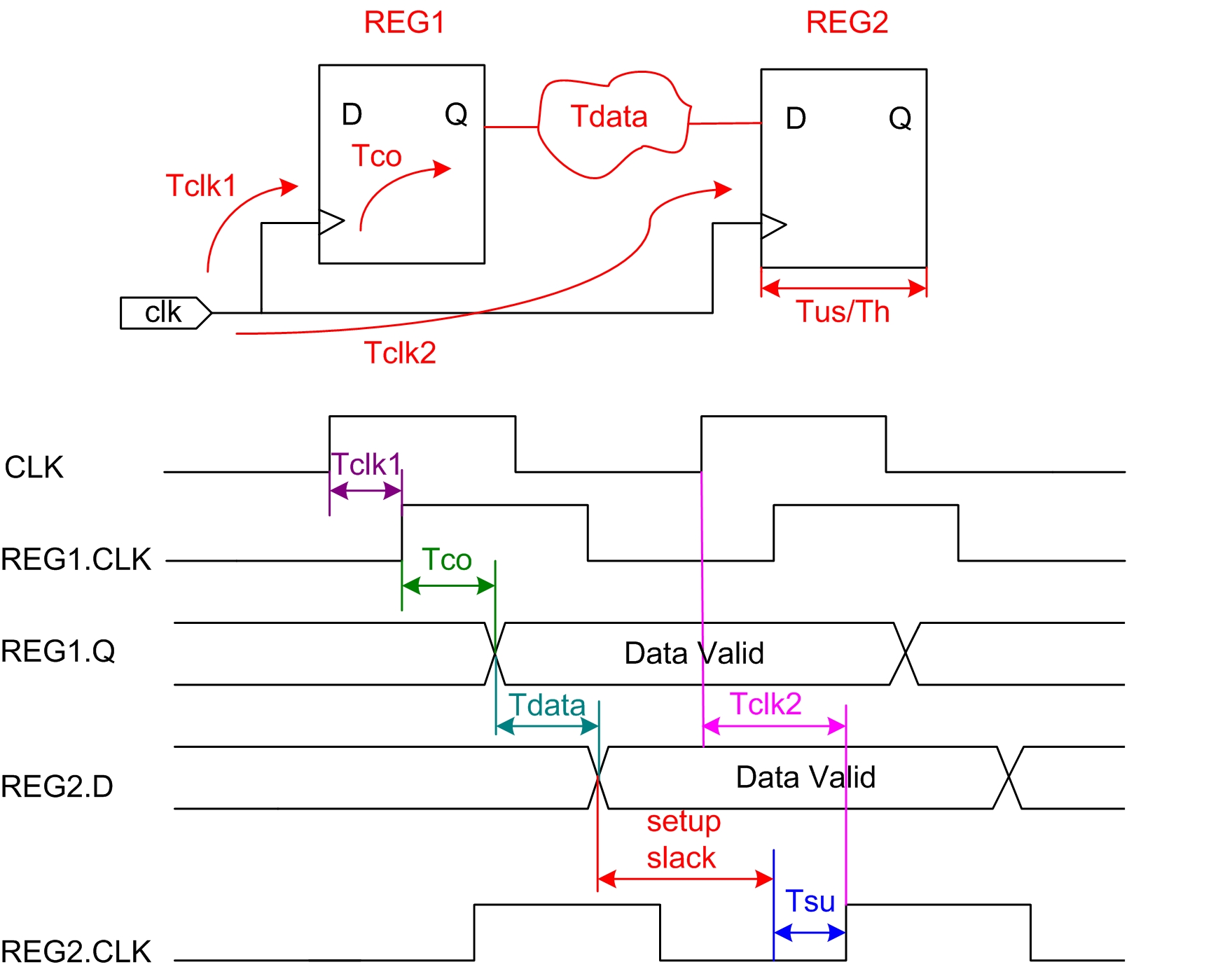
图3.8 建立时间余量
如图3.8所示,建立时间余量的计算公式如下:
Setup slack = Data Required Time - Data Arrival Time (公式2-6)
由公式可知,正的slack表示数据需求时间大于数据到达时间,满足时序(时序的余量),负的slack表示数据需求时间小于数据到达时间,不满足时序(时序的欠缺量)。
3.1.7 时钟最小周期
时钟最小周期:系统时钟能运行的最高频率。
1. 当数据需求时间大于数据到达时间时,时钟具有余量;
2. 当数据需求时间小于数据到达时间时,不满足时序要求,寄存器经历亚稳态或者不能正确获得数据;
3. 当数据需求时间等于数据到达时间时,这是最小时钟运行频率,刚好满足时序。
从以上三点可以得出最小时钟周期为数据到达时间等于数据需求时间,的运算公式如下:
Data Required Time = Data Arrival Time
图解Setup 与 Hold Slack
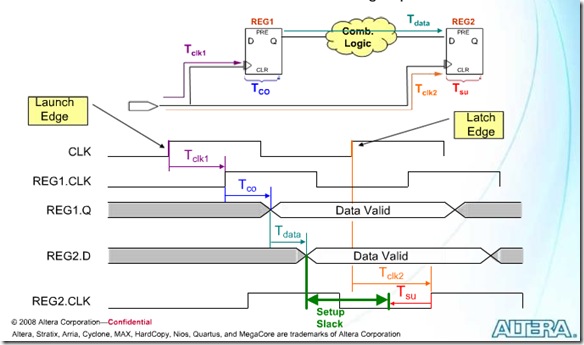
从上面两个图中可以清晰的看出Setup与Hold Slack的定义与计算方法:
Setup slack=latch edge+Tclk2-Tsu-(launch edge+Tclk1+Tco+Tdata)
=(latch edge-lanuch edge)+(Tclk2-Tclk1)-(Tsu+Tco+Tdata)
对于工具默认的单周期来说,latch edge-lanuch edge=T,如果不考虑时钟的skew,Tclk2-Tclk1=0,上式可以表达成:
Setup slack=T-(Tsu+Tco+Tdata),这就是为什么说源寄存器与目的寄存器之间延迟不能太长的原因,延迟越长,slack越小。
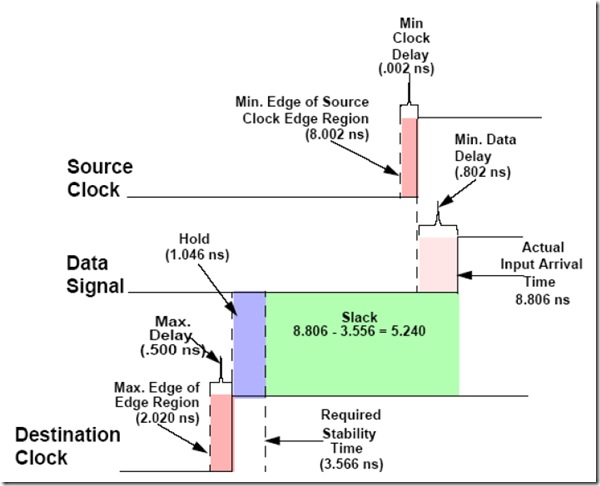
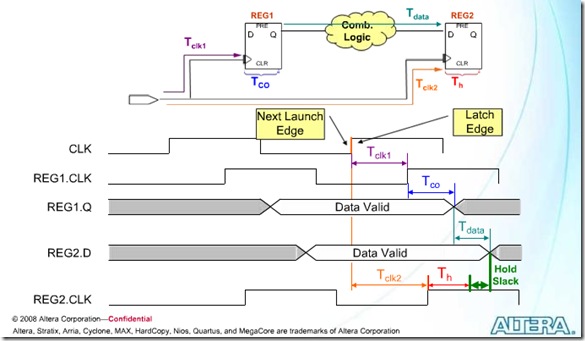
Hold slack=data arrival time – data required time
=(launch edge + Tclk1 + Tco + Tdata) – (latch edge + Tclk2 + Th)
=(launch edge – latch edge) – (Tclk2 – Tclk1) + (Tco + Tdata + Th)
注意,上式中的launch edge为next launch edge,即为latch edge,所以launch edge – latch edge=0,如果不考虑时钟的skew,Tclk2-Tclk1=0,上式可以表达成:
Hold slack=Tco + Tdata – Th,这就是为什么说源寄存器与目的寄存器之间延迟不能太短的原因,时间太短,slack越小。
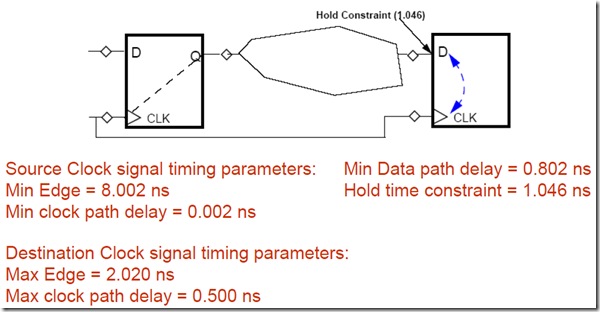
setup slack 计算

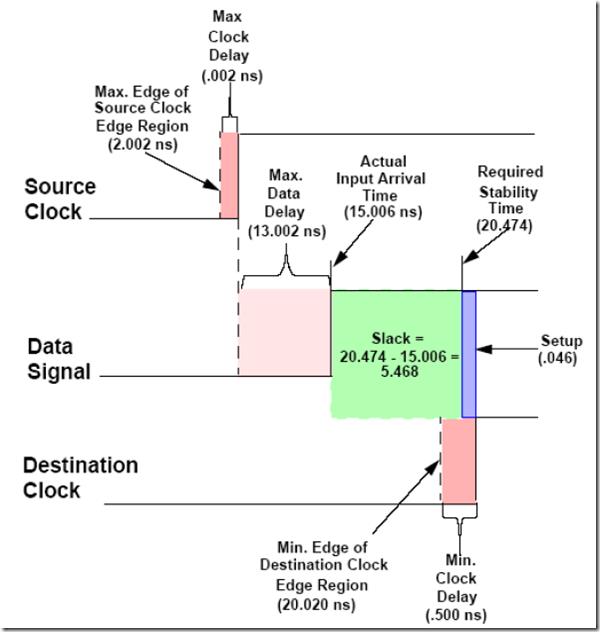
hold slack 计算