从零实现一个简单神经网络（全连接层）

Posted 2022-02-17 IsQtion

前向传播

首先我们需要先确定一个公式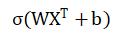

其中W是我们的权重，X是我们的输入，b是偏置, σ是激活函数
就拿最简单的两层神经网络来举例子，也就是由一个输入层，一个隐藏层，和一个输出层所组成的神经网络。在这个神经网络里，W也就是我们的隐藏层，X也就是输入层

假设现在我们的输入X是一个1xN的一维矩阵

假如我们需要实现0-9的手写数字识别功能，那么我们最后的输出就是0-9这十个数字的概率矩阵，也就是1x10的一个一维矩阵

那么应该如何将一个1xN的矩阵变成1x10的矩阵呢。
我们可以用一个10xN的矩阵，也就是隐藏层的W与X的转置矩阵做矩阵乘法，这样得出来的就是一个10x1的矩阵了，把结果再转置一下，就是我们所需要的最后结果了（实际情况中其实不需要再转置一下），最后再加上一个10x1维的偏置矩阵，这个线性变化就完成了。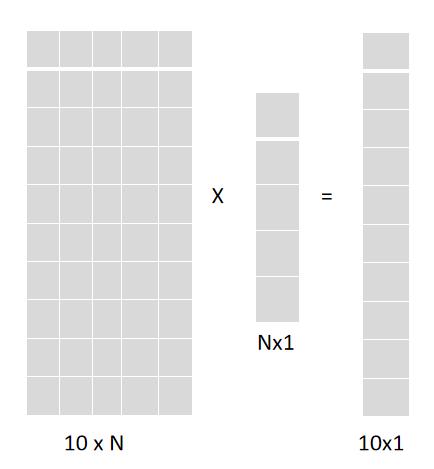

通常在线性变化之后，还会对输出的结果进行一次激活函数的运算，常用的激活函数有很多，比如：Sigmoid,Tanh,Relu,LeakRelu 等等。
线性变化+激活函数就完成了隐藏层的输出。最后，隐藏层的输出结果再与输出层的权重矩阵进行相同的操作，一个简单的2层神经网络的前向传播也就完成了

反向传播

将网络最后的输出结果，与我们的真值做运算就可以得到我们的这次训练的损失是多少了，常用的损失计算的方法也有很多，比如：平方损失，绝对值损失，交叉熵损失等等。
得到了损失值，我们就知道了这次网络的输出跟真实情况的差距有多大了，损失值越小代表我们的网络输出的结果越准确，为了能够实现这一目标，我们就需要根据损失，去更新每个隐藏层的权重矩阵和偏置矩阵，因为最后的输出结果就是输入的数据跟一层一层的隐藏层中的权重矩阵相运算所得到的，因此，隐藏层中的矩阵与最后输出结果的准确性有直接关系

这里假设我们的整个网络中所用到的激活函数是sigmoid，损失函数使用的是平方损失。那么现在我们来梳理一下这整个2层神经网络前向传播的过程。
首先，我们定义我们最开始的输入是X，隐藏层的权重矩阵是W，偏置是A，输出层的权重矩阵是V,偏置是B
那么整体的前向传播的数学表达式就应该是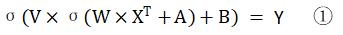

损失函数的表达式则是

其中y代表真值，也就是真值矩阵T中的每一项；y尖代表网络的输出，也就是①式Y矩阵中的每一项
而对于权重矩阵的更新用的则是梯度下降法，也就是利用链式求导法则，分别求出，L对W,V,A,B的导数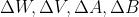,乘上学习率再加回原来的就完成了这次的更新。
首先让我们画张图来梳理一下，也方便后面的求导

我们可一先不把这些X,W,P,Q什么的当成矩阵，因为如果是矩阵的话，在运算过程中还要把这些矩阵转置过来转置过去的，可以把他们当成一个实数，这样对反向求导会更好理解一些。

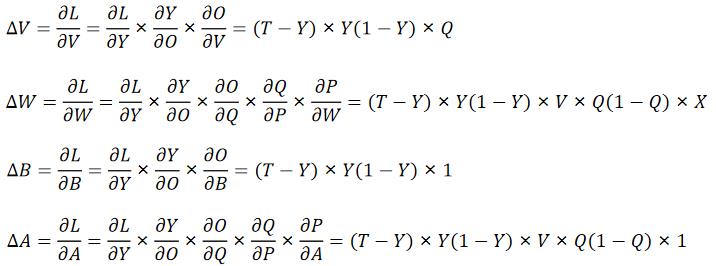
 其中σ(x)是sigmoid函数，σ(x)的导数 = σ(x)·[1-σ(x)]

代码实现

import numpy as np

class net:
    def __init__(self,input_nodes,hidden_nodes,output_nodes,learning_rate):
        self.input_nodes = input_nodes        #输入的节点数
        self.hidden_nodes = hidden_nodes      #隐藏层的节点数
        self.output_nodes = output_nodes      #输出的节点数
        self.learning_rate = learning_rate    #学习率

        self.activation_function = lambda x:1/(1+np.exp(-x))        #sigmoid激活函数

        self.w = np.random.randn(hidden_nodes,input_nodes)*0.01     #隐藏层的权重矩阵
        self.v = np.random.randn(output_nodes,hidden_nodes)*0.01    #输出层的权重矩阵
        self.b1 = np.array(np.zeros(hidden_nodes),ndmin=2).T        #隐藏层的偏置
        self.b2 = np.array(np.zeros(output_nodes),ndmin=2).T        #输出层的偏置
    def train(self,inputs,targets):
        inputs = np.asfarray(np.array(inputs,ndmin=2).T)            #将输入和真值矩阵转置一下
        targets = np.asfarray(np.array(targets,ndmin=2).T)

        hidden_level_input = np.dot(self.w,inputs)+self.b1          #WX+A = P
        hidden_level_output = self.activation_function(hidden_level_input)   #σ(P) = Q

        output_level_input = np.dot(self.v,hidden_level_output)+self.b2     #VQ+B = O
        output_level_output = self.activation_function(output_level_input)  #σ(O) = Y

        loss = 1/2*(np.sum(np.square(targets-output_level_output)))         #平方损失

        # 计算梯度
        G = (targets-output_level_output)*output_level_output*(1-output_level_output) #(T-Y)xY(1-Y) = G
        E = hidden_level_output*(1-hidden_level_output)*np.dot(self.v.T,G)            #GxVxQ(1-Q)
        self.v+=self.learning_rate*np.dot(G,hidden_level_output.T)
        self.w+=self.learning_rate*np.dot(E,inputs.T)
        self.b1+=self.learning_rate*E
        self.b2+=self.learning_rate*G