CSDN 年度征文｜回顾 2021，展望 2022Java版高级数据结构图论基础（DFS&BFS）

Posted 2022-02-14 chenry777

本文涉及代码见：https://github.com/chenruoyu0319/data-structure-for-java/tree/main/%E5%9B%BE%E8%AE%BA%E5%9F%BA%E7%A1%80%EF%BC%88DFS%26BFS%EF%BC%89

一、什么是图？

图（Graph）是一种非线性数据结构。可以说它是一种比较复杂的数据结构，它比树还要复杂。因为图没有层的概念，它们之间的任意元素都可能产生关系。

图的基本知识：

（1）顶点：图中的节点

（2）边：节点与节点之间的关系

（3）顶点的度：从该顶点出发，可以到达其他相邻节点的数量

（4）出度、入度：带方向的度

（5）有向图：有方向的图

（6）无向图：无方向的图

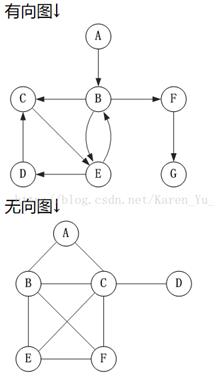
图的存储方式：

存储：可以用邻接矩阵或邻接表来存储

（1）邻接矩阵：

图里有x个点就是 x*x的矩阵。

比如A[1][1]：表示从1到1的情况，A[1][2]就表示1到2的情况，如果可达就存1，不可达就存0，最后表示成一个矩阵的情况，这个矩阵就是邻接矩阵，也是一个稀疏矩阵：

比如，

0 |0| 0

1 |1 |1

0 |1| 0

就是一个3*3的矩阵

（2）邻接表：数组+链表

这是一种数组+链表的形式，在一维数组中存储一个个链表来表示其与相邻节点的关系

A -> B

B -> C -> E -> F

C -> E

（3）以上两种对比：不同的情况要不同的解决

数组：浪费空间，但是速度块。数据不大，优先选用数组。

链表：节省空间，但是速度慢。

二、图遍历算法

我们要掌握的是最基础的2种遍历算法：

1.深度优先遍历（DFS）：大家可以想象玩迷宫，是不是选择一个方向走到底，直到不能走了你在返回一步继续试其他的方向，没错这其实就是深度优先遍历。一条路走到底，递归，有回溯。也要标记走过的点。

关键的优化:剪枝

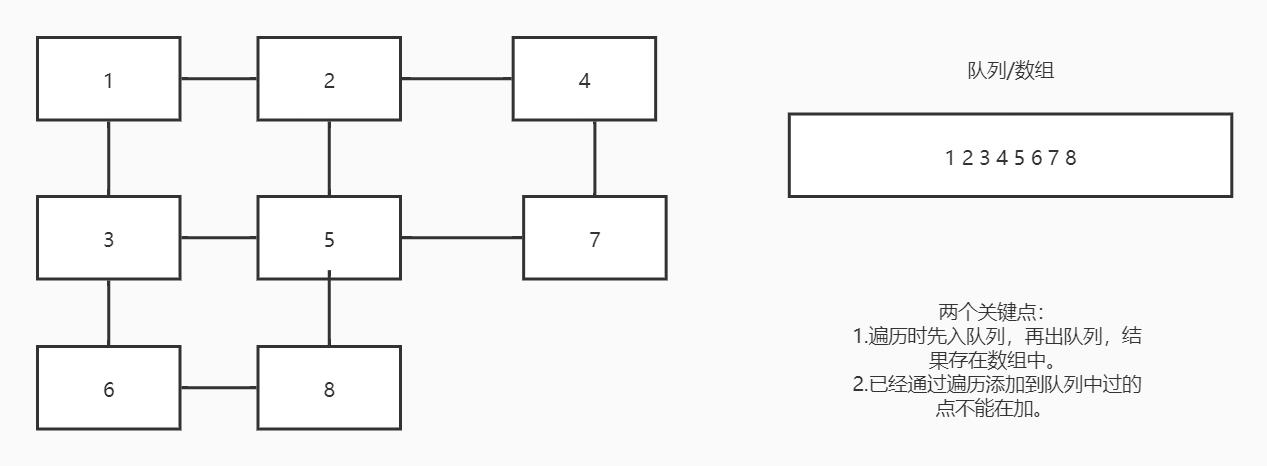
2.广度优先遍历（BFS）：类似于树结构的层次遍历，先找到一个点，然后把该点加入队列，依次找出该点的关联边加入队列，循环操作，一直到队列为空。

两个关键点：队列，标记数组，加过的点不能在加。

三、实例

解救美女1：有一天，小美和你去玩迷宫。但是方向感不好的小美很快就迷路了，你得知后便去

解救无助的小美，你已经弄清楚了迷宫的地图，现在你要知道从你当前位置出发你是否能够达到

小美的位置？

1:表示地图上的障碍物，0表示有路可走。我们可以构造一个映射这个图的邻接矩阵。

0(你) 0 1 0

0 0 0 0

0 0 1 0

0 1 0(小美) 0

0 0 0 1

可以用BFS算法解决。

参考代码：

class Point 

	int x;
	int y;

	public Point() 
	

	public Point(int x, int y) 
		this.x = x;
		this.y = y;
	

	@Override
	public String toString() 
		return "Point" +
				"x=" + x +
				", y=" + y +
				'';
	


public class BFS 

	int n; // 地图的行
	int m; // 地图的列
	int dx; // 安琪的位置x
	int dy; // 安琪的位置y
	int data[][]; // 邻接矩阵
	boolean mark[][]; // 标记数据 走过的位置

	public void bfs(int x, int y)  // x he y表示你当前的位置,就是求（x，y）->(dx,dy)能不能到
		if(x < 1 || x > n || y < 1 || y > m) return ;
		if(x == dx && y == dy) 
			System.out.println("true");
			return ;
		
		mark[x][y] = true;

		Queue<Point> queue = new ArrayBlockingQueue<Point>(n * m); // 因为最多也就是n*m个点
		Point start = new Point();
		start.x = x;
		start.y = y;
		queue.add(start);
		// 上 => 右 => 下 => 左, 顺时针遍历
		int next[][] =   0, 1 ,  1, 0 ,  0, -1 ,  -1, 0  ;	//ACM想到的

		while (!queue.isEmpty()) 		//O(n)
			Point point = queue.poll(); // 拿出队列的第一个点
			for(int i = 0 ; i < 4; i++) 
				int nextx = point.x + next[i][0];
				int nexty = point.y + next[i][1];
				if(nextx < 1 || nextx > n || nexty < 1 || nexty > m) continue;
				if(data[nextx][nexty] == 0 && !mark[nextx][nexty]) 		//表示可以走
					if(nextx == dx && nexty == dy) 		//表示可以到了 就不走了
						System.out.println("true");
						return ;
					
					Point newPoint = new Point();
					newPoint.x = nextx;
					newPoint.y = nexty;
					mark[nextx][nexty] = true;
					queue.add(newPoint);
				
			
			
		
		System.out.println("false");
		return ;

	

解救美女2：有一天，小美去玩迷宫。但是方向感不好的小美很快就迷路了，你得知后便去

解救无助的小美，你已经弄清楚了迷宫的地图，现在要你以最快的速度去解救小美，你能计算出

最快需要几步吗？最快的路径。

如果把题目换成求最快的路径，那么用BFS算法就会显得非常吃力，可以用DFS算法解决。

参考代码：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import java.util.Stack;

public class DFS 

    int n; // 地图的行
    int m; // 地图的列
    int dx; // 安琪的位置x
    int dy; // 安琪的位置y
    int data[][]; // 邻接矩阵
    int route[][]; // 路径矩阵

    int minStep = Integer.MAX_VALUE; // 要走的最小步数,求最小的数 你最开始是不是要赋值一个最大的数

    boolean mark[][]; // 标记数据 走过的位置
    int next[][] = 0, 1, 1, 0, 0, -1, -1, 0;

    // 使用栈保存最佳的路径
    Stack<Point> bestRoute = new Stack<>();
    // 保存所有的最短路径的集合
    List<Stack<Point>> routeList = new ArrayList<>();

    public DFS(int n, int m, int dx, int dy, int[][] data, boolean[][] mark) 
        this.n = n;
        this.m = m;
        this.dx = dx;
        this.dy = dy;
        this.data = data;
        this.mark = mark;
    

    public void dfs(int x, int y, int step)  // x,y表示我的位置，step,当前走过的路径长度

        if (x == dx && y == dy)         //枚举了所有的路径
            if (step < minStep) 
                minStep = step;
				routeList.clear();
                routeList.add((Stack<Point>) bestRoute.clone());
            
            return;
        
        for (int i = 0; i < 4; i++) 
			// 如果当前步数大于最小步数, 就没必要进行后面的判断了
			if (step +1 >minStep)
				break;
			
            int nextx = x + next[i][0];
            int nexty = y + next[i][1];
            if (nextx < 1 || nextx > n || nexty < 1 || nexty > m)
                continue;
            if (data[nextx][nexty] == 0 && !mark[nextx][nexty])  // 表示可以走 每个点都有4个方向，
                // 这里有三行代码
                mark[nextx][nexty] = true;
                bestRoute.push(new Point(nextx, nexty));
                dfs(nextx, nexty, step + 1);
                bestRoute.pop();
                // 回溯
                mark[nextx][nexty] = false;
            
        
    

    public static void main(String[] args) 
        Scanner cin = new Scanner(System.in);
        int n = 5;
		int m = 4;

        int data[][] = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) 
            for (int j = 1; j <= m; j++) 
                data[i][j] = cin.nextInt();
            
        
        int dx = cin.nextInt();
        int dy = cin.nextInt();

        boolean mark[][] = new boolean[n + 1][m + 1];
        int x = cin.nextInt();
        int y = cin.nextInt();

        mark[x][y] = true;        //我的起始位置
        DFS dfs = new DFS(n, m, dx, dy, data, mark);
        dfs.dfs(x, y, 0);
        System.out.println(dfs.minStep);
        System.out.println("==========找到的最短路径===========");
        for (Stack<Point> stack : dfs.routeList) 
            for (Point point : stack) 
				System.out.println(point);
			
			System.out.println("第二种情况: ");
        
    

/*
0 0 1 0
0 0 0 0
0 0 0 0
0 1 0 0
0 0 0 1
4 3
1 1
 * 
 */

四、图的应用

社交网络: QQ推荐

知图谱: 推荐算法，数据挖掘

图数据库: Neo4j

路径。

如果把题目换成求最快的路径，那么用BFS算法就会显得非常吃力，可以用DFS算法解决。