牛牛做数论（素数+思维）

Posted 2022-02-12 MangataTS

题目链接

https://ac.nowcoder.com/acm/contest/23106/D

题面

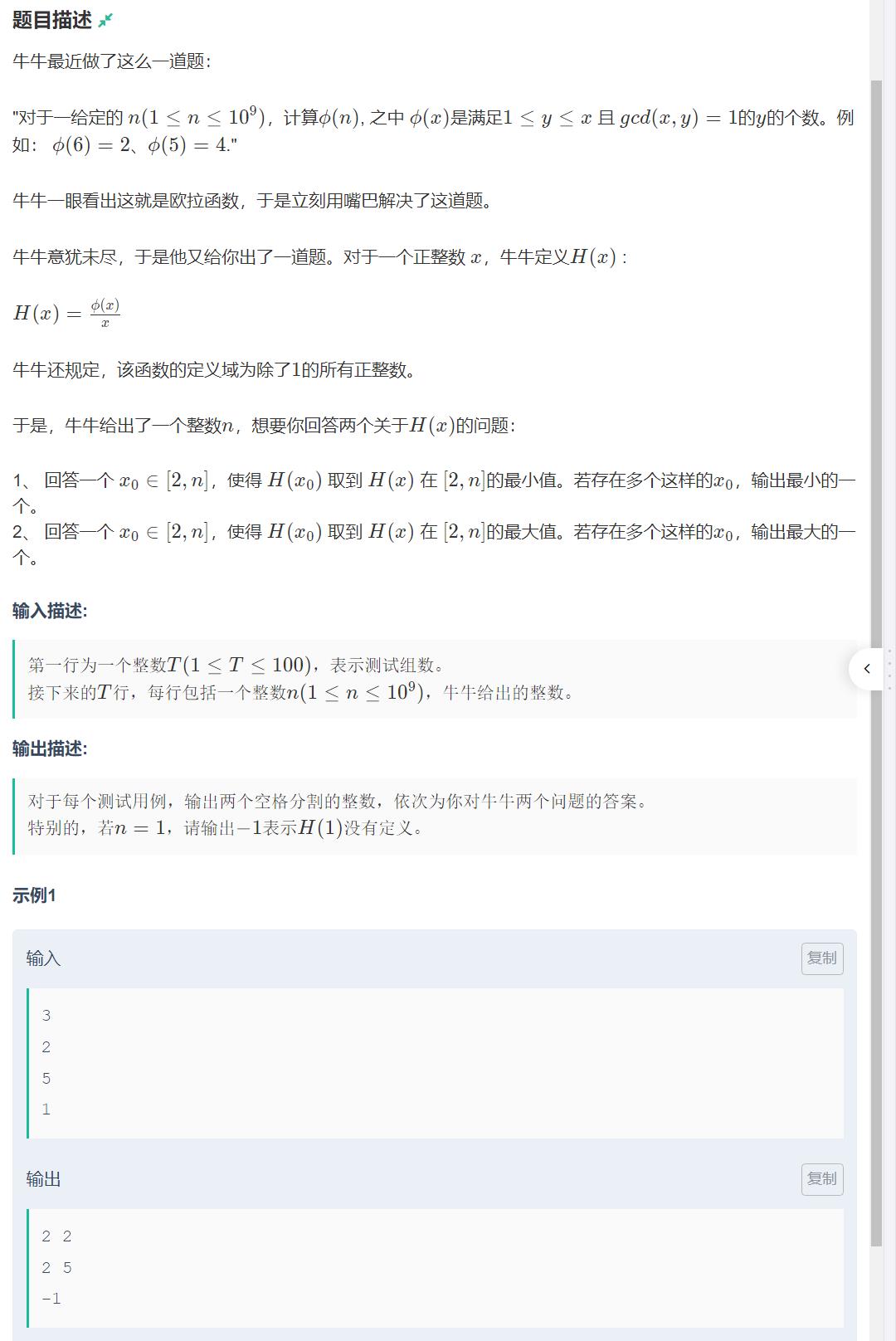
思路

结论

对于问题一：为2、2×3、2×3×5、2×3×5×7…这些前若干个素 数的积中，最大的且不超过n的那一个，如n=233，则答案为 2×3×5×7=210

对于问题二：为[2,n]中最大的素数

如果n为1，直接输出-1

想法

对于问题一，我们要求一个使得$H(x)$最小的x，那么我们希望Font metrics not found for font: .尽可能地小，x尽可能的大，那么x一定不能是素数，因为这样的话就是最大情况了，那么我们通过前缀素数积其实就能实现我们的想法，因为互质的个数就是其因子数，所以我们就得到了问题一的思路

对于问题二，我们要求一个使得H(x)最小的x，不难发现其实就是找小于等于n的最大的质数就好了，因为H(x)∈(0,1)的，当我们选取的x是一个质素的时候就找到了$\frac{x-1}{x}=1-\frac{1}{x}$，那么我们想让这个值最大化，也就是x要选大点，所以就是小于n的素数咯，关于[0,1e9]的素数判定，其实这里有个小知识，$10^9$以内的素数最大间隔是282，所以我们最多只需要判定282次数就好啦

详情请看代码

代码

#include<bits/stdc++.h>
using namespace std;
//----------------自定义部分----------------
#define ll long long
#define mod 1000000007
#define endl "\\n"
#define PII pair<int,int>

int dx[4]=0,-1,0,1,dy[4]=-1,0,1,0;

ll ksm(ll a,ll b) 
	ll ans = 1;
	for(;b;b>>=1LL) 
		if(b & 1) ans = ans * a % mod;
		a = a * a % mod;
	
	return ans;


ll lowbit(ll x)return -x & x;

const int N = 2e6+10;
//----------------自定义部分----------------
ll n,m,q,a[N];
ll b[20]=2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71;
bool is_prime(ll x)
	for(ll i  = 2LL;i * i <= x; ++i) 
		if(x % i == 0) return false;
	
	return true;


int main()

//	std::ios::sync_with_stdio(false);
//	std::cin.tie(nullptr);
//	std::cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--) 
		cin>>n;
		if(n == 1)
			cout<<-1<<endl;
			continue;
		
		ll res = 1;
		for(int i = 0;i < 20 && res * b[i] <= n; ++i) 
			res *= b[i];
		
		ll ans = n;
		for(;ans >= 0; --ans) 
			if(is_prime(ans)) break;
		
		cout<<res<<" "<<ans<<endl;
	
	
	return 0;