.设一棵二叉树的深度为k,则该二叉树中最多有( )个结点.

Posted 2023-05-10

一颗深度为k的二叉树，最多有(2^k)-1个节点，第k层最大节点数为2^（k-1）次方。

性质1：二叉树的第i层上至多有2i-1（i≥1）个节点。

性质2：深度为h的二叉树中至多含有2h-1个节点。

性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1。

性质4：具有n个节点的完全二叉树深为log2x+1（其中x表示不大于n的最大整数）。

扩展资料：

线索二叉树

按照某种遍历方式对二叉树进行遍历，可以把二叉树中所有结点排列为一个线性序列。在该序列中，除第一个结点外，每个结点有且仅有一个直接前驱结点；除最后一个结点外，每个结点有且仅有一个直接后继结点。

但是，二叉树中每个结点在这个序列中的直接前驱结点和直接后继结点是什么，二叉树的存储结构中并没有反映出来，只能在对二叉树遍历的动态过程中得到这些信息。

为了保留结点在某种遍历序列中直接前驱和直接后继的位置信息，可以利用二叉树的二叉链表存储结构中的那些空指针域来指示。这些指向直接前驱结点和指向直接后继结点的指针被称为线索（thread），加了线索的叉树称为线索二叉树。

参考技术A 一颗深度为k的二叉树,最多有(2^k)-1个节点,第k层最大节点数为2^（k-1）次方

数据结构－二叉树

二叉树

在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至多有2k-1个叶子节点，至多有2k-1个节点。

 

类型

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

                   
 

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

                   

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 

 

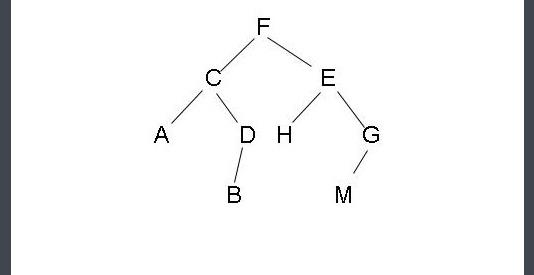
二叉树的遍历和创建

 

from collections import deque


class BitTreeNode:
    def __init__(self,data):
        self.data=data
        self.lchild = None #左孩子
        self.rchild = None #右孩子


a = BitTreeNode(‘A‘)
b = BitTreeNode(‘B‘)
c = BitTreeNode(‘C‘)
d = BitTreeNode(‘D‘)
e = BitTreeNode(‘E‘)
f = BitTreeNode(‘F‘)
g = BitTreeNode(‘G‘)

e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f


root = e  #根节点
# print(root.lchild.rchild.data)

#前序遍历
def pre_order(root):
    if root :     #——访问根结点的操作发生在遍历其左右子树之前。
        print(root.data,end=‘,‘)
        pre_order(root.lchild)
        pre_order(root.rchild)

# pre_order(root)


# 中序遍历
def in_order(root):
    if root :
        in_order(root.lchild)   #root左孩子
        print(root.data,end=‘,‘)#root本身
        in_order(root.rchild)   #root右孩子

# in_order(root)

# 后序遍历

def post_order(root):
    if root:
        post_order(root.lchild)
        post_order(root.rchild)
        print(root.data,end=‘,‘)

# post_order(root)

#层序遍历
def level_order(root):
    queue = deque()
    queue.append(root)
    while len(queue)>0:
        node = queue.popleft()
        print(node.data,end=‘,‘)
        if node.lchild:
            queue.append(node.lchild)
        if node.rchild:
            queue.append(node.rchild)


level_order(root)

 二叉树的插入.查询.和删除

 

‘‘‘插入数据到树‘‘‘
class BiTreeNode:
    def __init__(self,data):  #这样传参也可以?
        self.data=data
        self.lchild = None
        self.rchild = None
        self.parent = None

class BST :
    def __init__(self,li=None):
        self.root = None
        if li :
            for val in li:
                self.insert_no_rec(val)



    def insert(self,node,val):
        if not node:
            node = BiTreeNode(val)   #不存在创建树和赋值node
        elif val<node.data:    # 查找的数val小于选择的树node
            node.lchild = self.insert(node.lchlid,val)#左子树插入val
            node.lchild.parent = node   #链接为node子树

        elif val>node.data :
            node.rchild = self.insert(node.lchlid,val)
            node.rchild.paret = node

        return node


    def insert_no_rec(self,val):  #循环
        p = self.root
        if not p:
            self.root = BiTreeNode(val)   #根节点
            return
        while True:
            if val < p.data :               #比根小左根的左子节点
                if p.lchild:
                    p = p.lchild
                else:                        #左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p= p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return


    def query(self,node,val):
        if not node:
            return None
        if node.data<val:
            return self.query(node.rchile,val)
        elif node.data>val:
            return self.query(node.lchild,val)
        else:
            return node

    def query_no_rec(self,val):
        p = self.root
        while p:
            if p.data < val:
                p=p.rchild
            elif p.data > val :
                p = p.lchild
            else:
                return p
        return None


    def pre_order(self,root):
        if root:  # ——访问根结点的操作发生在遍历其左右子树之前。
            print(root.data, end=‘,‘)
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)


    def in_order(self,root):
        if root:
            self.in_order(root.lchild)  # root左孩子
            print(root.data, end=‘,‘)  # root本身
            self.in_order(root.rchild)  # root右孩子


    def post_order(self,root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=‘,‘)


    def __remove_node_1(self,node):
        #情况一：node是叶子节点
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  #node是他父亲的左孩子
            node.parent.lchild = None    #将node父亲的左孩子也就是node滞空
        else:
            node.parent.rchild = None

    def __remove_node_21(self, node):
        #情况2.1:node只有一个左孩子
        if not node.parent:             #node没有父亲也就是根节点
            self.root = node.lchild     #node被删除node的左儿子上位
            node.lchild.parent = None   #原node位置滞空
        elif node == node.parent.lchild :
            node.parent.lchild = node.lchild   #node父亲的左孩子＝node的左孩子
            node.lchild.parent = node.parent
        else:
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        #情况2.1:node只有一个右孩子
        if not node.parent:
             self.root = node.rchild
        elif node == node.parent.lchild :
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent


    def delete(self,val):
        if self.root: #不是空树
            node = self.query_no_rec(val)
            if not node:
                return False
            if not node.lchild and not node.rchild : #叶子节点
                self.__remove_node_1(node)
            elif not node.rchild :                  #只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild :                  #只有一个右孩子
                self.__remove_node_22(node)
            else:                                   #两个孩子都有
                min_node = node.rchild
                while min_node.lchild :
                    min_node = min_node.lchild
                node.data = min_node.data
                                                    #删除min_node
                if min_node.rchild :
                    self.__remove_node_22(min_node)
                else:
                    self.__remove_node_1(min_node)







tree = BST([2,3,4,1,6,7,9,5,8]) #建树
# tree.post_order(tree.root)
# print(‘‘)
tree.in_order(tree.root)
print(‘‘)
# tree.post_order(tree.root)


# print(tree.query_no_rec(3).data)  #查找

tree.delete(4)
tree.in_order(tree.root)