ABC235 F Variety of Digits

Posted 2022-02-06 solemntee

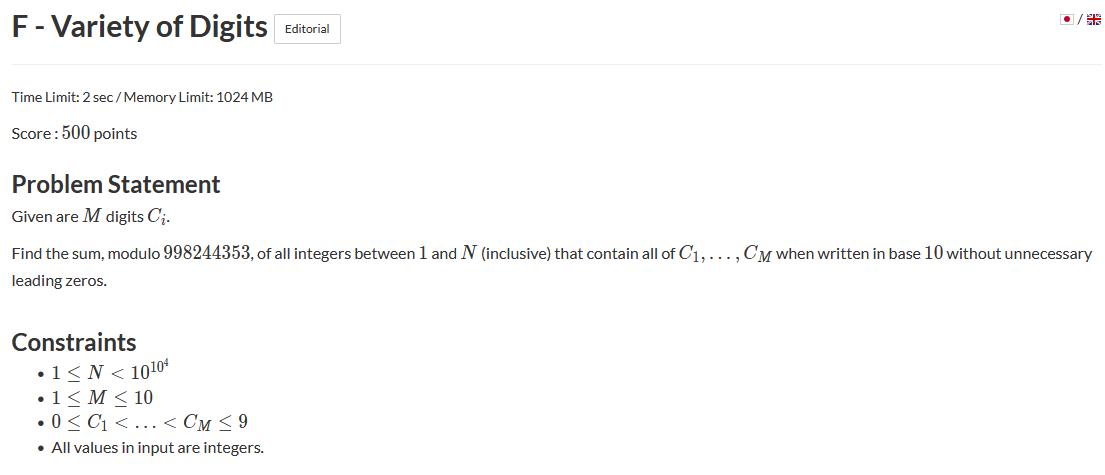
题意：给一个小于$10^{10^4}$的整数$N$找不大于$N$的满足数位中有$c_1...c_n$的数字。
考虑数位$dp$，$dp[pos][sta]$表示第$pos$位，数位中已经出现的数字种类情况是$sta$的方案数，$dp2[pos][sta]$表示第$pos$位，数位中已经出现的数字种类情况是$sta$的贡献和，总体来讲是非常经典的题目。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int limit[10005];
ll dp[10005][3005];
ll dp2[10005][3005];
int M,c[14];
int mp[10];
char s[10005];
const int mod=998244353;
ll P[10005];
void init()

    P[0]=1;
    for(int i=1;i<=10000;i++)P[i]=P[i-1]*10%mod;

pair<ll,ll> dfs(int pos,int sta,bool lead,bool flag)

    if(pos==-1)
        return sta==((1<<M)-1),0;
    
    if(!flag&&!lead&&dp[pos][sta]!=-1)return dp[pos][sta],dp2[pos][sta];

    ll sum1=0,sum2=0,up=flag?limit[pos]:9;

    for(ll i=0;i<=up;i++)
    
        if(lead&&i==0)
        
            pair<ll,ll>p=dfs(pos-1,sta,true,flag&&i==limit[pos]);
            sum1=(sum1+p.first)%mod;
            sum2=(sum2+P[pos]*i%mod*p.first%mod+p.second)%mod;
        
        else if(mp[i]!=0)
        
            pair<ll,ll>p=dfs(pos-1,sta|(1<<(mp[i]-1)),false,flag&&i==limit[pos]);
            sum1=(sum1+p.first)%mod;
            sum2=(sum2+P[pos]*i%mod*p.first%mod+p.second)%mod;
        
        else
        
            pair<ll,ll>p=dfs(pos-1,sta,false,flag&&i==limit[pos]);
            sum1=(sum1+p.first)%mod;
            sum2=(sum2+P[pos]*i%mod*p.first%mod+p.second)%mod;
        
    
    if(!flag&&!lead)
    
        dp[pos][sta]=sum1;
        dp2[pos][sta]=sum2;
    

    return sum1,sum2;

int main()

    init();
    memset(dp,-1,sizeof(dp));
    memset(dp2,-1,sizeof(dp2));
    scanf("%s",s);
    int len=strlen(s);
    for(int i=0;i<len;i++)limit[i]=s[len-i-1]-'0';
    scanf("%d",&M);
    int asdf=0;
    for(int i=1;i<=M;i++)
    
        scanf("%d",&c[i]);
        mp[c[i]]=++asdf;
    

    printf("%lld\\n",dfs(len-1,0,true,true).second);
    return 0;

/*
104
2
0 1

301
301
2
0 1

300
300
2
0 1

299
299
2
0 1
*/