「二分类算法」提供银行精准营销解决方案

Posted 2023-05-08

参考技术A 本练习赛的数据，选自UCI机器学习库中的「银行营销数据集(Bank Marketing Data Set)」
这些数据与葡萄牙银行机构的营销活动相关。这些营销活动以电话为基础，一般，银行的客服人员需要联系客户至少一次，以此确认客户是否将认购该银行的产品（定期存款）。
因此，与该数据集对应的任务是「分类任务」，「分类目标」是预测客户是(' 1 ')或者否(' 0 ')购买该银行的产品。

plot_depth_score(np.arange(10, 24))

plot_rs_score(np.arange(70, 90, 1))

Make a scorer from a performance metric or loss function.

This factory function wraps scoring functions for use in GridSearchCV
and cross_val_score. It takes a score function, such as accuracy_score ,
mean_squared_error , adjusted_rand_index or average_precision
and returns a callable that scores an estimator's output.
从性能指标或损失函数中进行记分。
此工厂函数包装用于GridSearchCV的评分函数
并交叉得分。它有一个记分函数，比如“精确记分”，
均方误差````调整后的 兰德 指数``或``平均 精度``
并返回一个可调用的值，该值对估计器的输出进行评分。

基于Multiple treatment的营销评估算法

营销是发现或挖掘准消费者和众多商家需求，通过对自身商品和服务的优化和定制，进而推广、传播和销售产品，实现最大化利益的过程。例如，银行可通过免息卡或降价对处在分期意愿边缘的用户进行营销，促使其分期进而提升整体利润；选择最优时机和地点对用户进行广告投放提升转化。

在大数据和“千人千面”的背景下，营销升级为“精准营销”，对每个用户的需求进行更加精细的个性化分析与投放，进而实现用户满意，广告主和平台获益的多赢局面。营销算法的步骤一般为：1) 圈人，2) 召回和排序 3) 在预算约束下，通过最大化ROI或利润uplift确定最终策略。

营销算法与传统的推荐召回的评估方法不尽相同，推荐召回等可通过CTR，准确率，AUC等方式进行评估。但营销的评估会更复杂，有以下四方面的难题：

1. 要以提升整体利润和用户满意度为目标，甚至还要考虑长远收益，不是简单的二分类或回归问题
2. 营销通常包含有多种决策，且比推荐更复杂的策略流程，其最终效果取决于策略和整体流程的最优化
3. 营销一般有预算限制，并要考虑投入产出比
4. 根本原因是：相比于分类等问题，知道当前决策对于任何个体是否是最优的几乎是不可能的，因为其响应在特定决策下是不可观测的。例如发放免息券，我们只能对某个个体在单一时间发放某一类特定的免息券，但无法在事先就知道这种决策就是最优的。重复实验在个体上是不可能实现的。因此，即使是从随机试验中获取的数据，在概率视角上也是unlabeled，因为即使在训练集上，在最优决策下试图预测的真实值（如响应率等）都是未知的。

由于成本原因，不可能做大量的随机实验。然而在做A/B test时，依然需要类似AUC等明确且容易解释的业务指标来评估营销算法模型好坏。但是，是否有较准确的评估营销算法性能的方法？

在此背景下，我们实现了multiple treatment（多决策评估）算法，其思路来自于论文《Uplift Modeling with Multiple Treatments and General Response Types》，该算法实现简单，理论完备，具有类似AUC一样优良的直观和可对比性。同时model-free，与具体所用的算法和策略无关。

我们会给出其容易理解的业务解释，补充其使用必要条件，完善理论推导。

多treatment的简单图例说明

我们先给出最简单的一个营销方案，来图示讲解该算法的原理。

对所有用户，有两种策略：原价/降价，在进行算法实验前，先进行了一轮小流量随机投放实验，两种策略投放比例各占50%。我们提出一种最简单的阈值策略：“低响应用户降价，高响应用户原价”，之后需要评估该策略的线上利润率。

如上图所示，纵轴为响应率轴，横轴为随机轴。随机实验与策略有两块重叠部分，即图3。由于重叠部分是历史已知可观测的，因此评估其重叠部分的利润率，即可代表整体策略的利润率。

仔细思考整个方法，思路非常简单，即使用无偏的部分样本的特性和统计量去代表整体，这几乎是初中数学的知识。只要样本足够多，其历史回测完全可以接近真实线上的效果。

该方法虽然想法很朴素，但必须注意一些很容易被忽略的条件：

1. 随机样本的数量即各块的面积要足够大，从而避免异常或特殊样本对整体评估效果的影响。
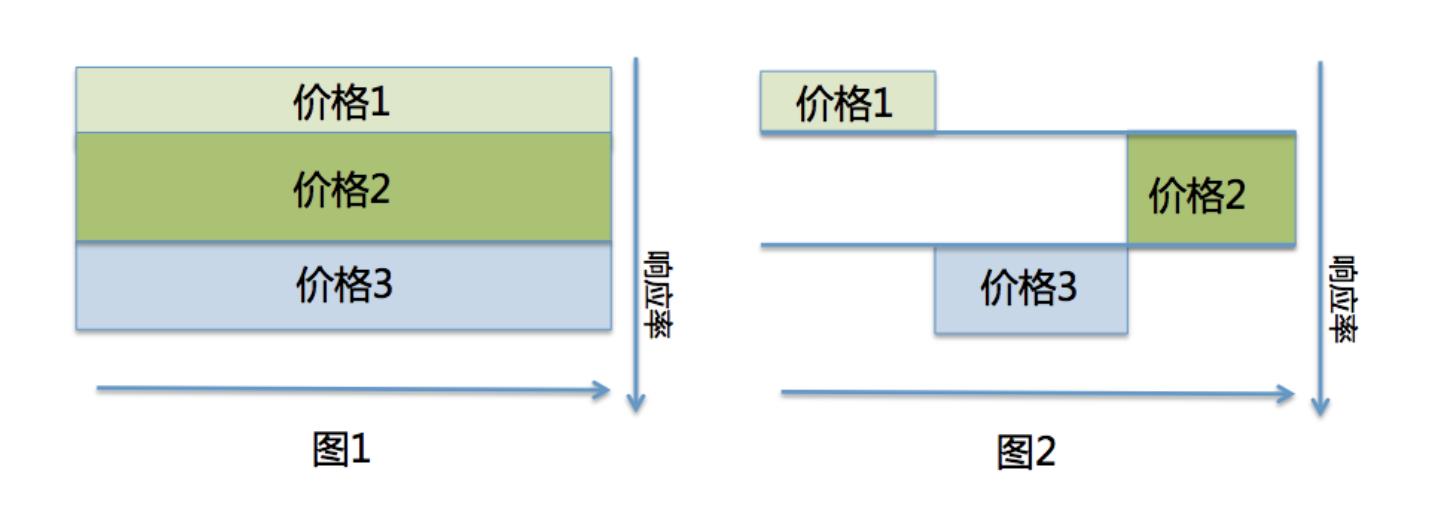
2. 随机实验必须随机且不同treatment的投放比例需一致，但真实投放时各treatment不需平均分配。下图解释了其原因：
   
3. 各treatment需要离散且数量远小于样本数，且各自独立（不过很难想象各treatment之间不独立的情形）
4. 需要使用最近的历史数据才能相对准确，要求环境必须有一定的平稳性，否则基于历史数据的回测就没有了意义。

再将其扩展为的多种treatment的复杂情形。若针对响应率进行多分段决策，则不需证明就能保证各决策在图中一定是直线且互相平行，与随机轴正交（否则策略就有猜测随机的能力），如下图所示：

若策略不仅需要考虑响应率，还需考虑其他指标如职业，则可以增加一条坐标轴代表职业，也一定与随机轴正交，构成高维线性空间，命中部分变为空间中的小区块，对区块的汇总依然能代表整体策略的利润率。值得注意的是，职业不一定需要需要响应率正交。

理论推导

一个uplift模型将整个特征空间分割为多个子空间，每个空间代表一种策略。在随机试验中，是能够获取一个样本随机落入某个子空间（即命中）的概率和其对应的响应的。因此通过计算整体命中子空间的响应，就能获取整体特征空间的真实响应。

在随机实验中，令K为所有可能的treatment数量，令\\(p_t\\)代表一个treatment等于t的概率，在任何有意义的场合，都能保证\\(p_t>0 \\ for \\ t=0,...K\\)

下面的论文截图给出了一个引理：

对一组随机实验数据\\(s_N = {(x^{(i)}, t^{(i)}, y^{(i)}, i = 1,2,..., N )}\\)， 计算\\(z{(i)}\\)是很容易的。如果\\(ith\\)个样本正好匹配了真实的treatment，则\\(z{(i)}= y^{(i)}/p_{t}\\), 即真实响应会被该treatment的概率所缩放，否则\\(z{(i)}\\)总为0。 由于对样本的平均就是对期望值的无偏估计，因此我们有如下的概念：

进一步地，可以计算z均值的置信区间，来帮助我们估计\\(E[Y|T=h(X)]\\)的置信度。 此处可以参考显著性检验的相关文章（如这篇）

如何对长期收益进行计算和建模？

虽然思路简单，易于实现，多treatment评估也只能解决短期决策评估，但用户和环境是时变的，当用户接受多个treatment(如降价奖励，红包或提价)之后，心智会发生改变，短期最大化收益不代表长期收益。

假设某一种策略被实施多次，我们已经能够观察到单个用户/群体的长程treatment和response，如何使用强化学习对时序信息进行建模？如何准确有效地对长程收益进行评估？这些都是非常有趣的问题。

有任何问题，欢迎讨论。