matlab遗传算法的程序中SOL是啥意思?

Posted 2023-05-08

【问题】在－5<=Xi<=5,i=1,2区间内，求解
f(x1,x2)=-20*exp(-0.2*sqrt(0.5*(x1.^2+x2.^2)))-exp(0.5*(cos(2*pi*x1)+cos(2*pi*x2)))+22.71282的最小值。
【分析】种群大小10，最大代数1000，变异率0.1,交叉率0.3
【程序清单】
％源函数的matlab代码
function [eval]=f(sol)
numv=size(sol,2);
x=sol(1:numv);
eval=-20*exp(-0.2*sqrt(sum(x.^2)/numv)))-exp(sum(cos(2*pi*x))/numv)+22.71282;
%适应度函数的matlab代码
function [sol,eval]=fitness(sol,options)
numv=size(sol,2)-1;
x=sol(1:numv);
eval=f(x);
eval=-eval;
%遗传算法的matlab代码
bounds=ones(2,1)*[-5 5];
[p,endPop,bestSols,trace]=ga(bounds,'fitness')

注：前两个文件存储为m文件并放在工作目录下，运行结果为
p =
0.0000 -0.0000 0.0055

这个程序里SOL代表什么意思?

是把一个矩阵编程一行，然后再把一行变成一个矩阵，是编码和解编码的过程。
指的种群中的一个个体的数值，相当于把初始种群中一个个体的变量拿出来，赋值给x。然后再用x去求适应度函数fitness。 参考技术A SOL，估计是阵列吧。本回答被提问者采纳

matlab基于多层编码遗传算法的车间调度算法matlab优化算法十九

基于多层编码遗传算法的车间调度算法

理论基础

遗传算法具有较强的问题求解能力，能够解决非线性优化问题。遗传算法中的每个染色体表示问题中的一个潜在最优解，对于简单的问题来说，染色体可以方便地表达问题的潜在解，然而，对于较为复杂的优化问题，一个染色体难以准确表达问题的解。多层编码遗传算法把个体编码分为多层，每层编码均表示不同的含义，多层编码共同完整表达了问题的解，从而用一个染色体准确表达出了复杂问题的解。多层编码遗传算法扩展了遗传算法的使用领域，使得遗传算法可以方便用于复杂问题的求解。

问题描述

车间调度是指根据产品制造的合理需求分配加工车间顺序，从而达到合理利用产品制造资源、提高企业经济效益的目的。车间调度问题从数学上可以描述为有n个待加工的零件要在m台机器上加工，车间调度的数学模型如下：
（1）机器集M={m1，m2，…，mm}，m，表示第j台机器，j=1,2，…，m。
（2）零件集P={p1，p2，…，pn}，p；表示第i个零件，i=1,2，…，n
（3）工序序列集OP={op1，op2，…，opn}，op，={opa,op2，…，opk}表示零件p的工序序列。
（4）可选机器集OPM={op1，opa，…，op4}），op，={op21，op2，…，opa}表示零件p的工序j可以选择的加工机器。
（5）使用机器加工零件的时间矩阵T,t∈T，表示第i个零件p，使用第j个机器的时间。
（6）使用机器加工零件的费用矩阵C,c∈C表示第i个零件p使用第j个机器的加工费用。
另外，问题需要满足的条件包括每个零件的各道工序使用每台机器不多于1次，每个零件都按照一定的顺序进行加工车间调度问题具有普遍性、复杂性、动态模糊性、多约束性等难点，一般可用优化调度算法和启发式求解，本案例采用多层编码遗传算法求解车间调度问题。

模型建立

基于多层编码遗传算法的车间调度算法流程所示。其中，种群初始化模块初始化种群构成问题的初始解集；适应度值计算模块计算染色体的适应度值；选择操作采用轮盘赌法选择优秀个体；交叉操作采用整数交叉法得到优秀个体；变异操作采用整数变异法得到优个体

算法实现

1.个体编码染色体编码方式为整数编码，每个染色体表示全部工件的加工顺序，当待加工的工件总数为n，工件n的加工工序共为m，时，则个体表示为长度为2∑n,m，的整数串。其中，染色体的前半部分表示所有工件在机器上的加工顺序，后半部分表示工件每道工序的加工机器序号。
如个体
【2431123421332213】
该个体表达了4个加工工序都是2次的工件在3台机器上的加工顺序。其中，前8位表示工件的加工顺序，为工件2→工件4→工件3→工件1→工件1→工件2→工件3→工件4；9到16位表示加工机器，依次为机器2→机器1→机器3→机器3→机器2→机器2→机器1→机器3。
2.适应度值染色体的适应度值为全部工件的完成时间，适应度值计算公式为fitness（i）= time其中，time指全部任务完成时间，全部工件完成时间越短，该染色体越好
3.选择操作选择操作采用轮盘赌法选择适应度较好的染色体，个体选择概率为pi（i）= Fitness（i）/>Fitness（i）
Fitness（i）=1/fitness（i）
其中，pi（i）表示染色体i在每次选择中被选中的概率
4.交叉操作种群通过交叉操作获得新染色体，从而推动整个种群向前进化，交叉操作采用整数交叉法。交叉操作首先从种群中随机选取两个染色体并取出每个染色体的前∑nm，位然后随i=1机选择交叉位置进行交叉。操作方法如下：交又位置为5，只对个体前∑nm，位进行交叉。
个体-【112322331112121222】交叉【22132231112121222】
极值-【221331213112212111】
【11233121312212111】
交叉后某些工件的工序多余（如个体中的工件2），某些工件的工序缺失（如个体中的工件1），因此，把工件工序多余的操作变为工件工序缺失的操作，并按交叉前个体的操作机器来调整个体（∑nm，+1）位到2∑nm，位的加工机器，如下所示：
交叉后个体-【221322331112121222】-【2213123311122222】

代码展示

%% 清空环境
clc;clear

%% 下载数据
load scheduleData Jm T JmNumber
%工序 时间

%% 基本参数
NIND=40;        %个体数目
MAXGEN=500;      %最大遗传代数
GGAP=0.9;       %代沟
XOVR=0.8;       %交叉率
MUTR=0.6;       %变异率
gen=0;          %代计数器
%PNumber 工件个数 MNumber  工序个数
[PNumber MNumber]=size(Jm);  
trace=zeros(2, MAXGEN);      %寻优结果的初始值
WNumber=PNumber*MNumber;     %工序总个数

%% 初始化
Number=zeros(1,PNumber);     % PNumber 工件个数
for i=1:PNumber
    Number(i)=MNumber;         %MNumber工序个数
end

% 代码2层，第一层工序，第二层机器
Chrom=zeros(NIND,2*WNumber);
for j=1:NIND
    WPNumberTemp=Number;
    for i=1:WNumber
        
        %随机产成工序
        val=unidrnd(PNumber);
        while WPNumberTemp(val)==0
            val=unidrnd(PNumber);
        end
        
        %第一层代码表示工序
        Chrom(j,i)= val;
        WPNumberTemp(val)=WPNumberTemp(val)-1;
        
        %第2层代码表示机器
        Temp=Jm{val,MNumber-WPNumberTemp(val)};
        SizeTemp=length(Temp);
        %随机产成工序机器
        Chrom(j,i+WNumber)= unidrnd(SizeTemp);
        
    end
end
 
%计算目标函数值
[PVal ObjV P S]=cal(Chrom,JmNumber,T,Jm);  

%% 循环寻找
while gen<MAXGEN
    
    %分配适应度值
    FitnV=ranking(ObjV);  
    %选择操作
    SelCh=select('rws', Chrom, FitnV, GGAP);       
    %交叉操作
    SelCh=across(SelCh,XOVR,Jm,T);          
    %变异操作
    SelCh=aberranceJm(SelCh,MUTR,Jm,T);            
    
    %计算目标适应度值
    [PVal ObjVSel P S]=cal(SelCh,JmNumber,T,Jm);   
    %重新插入新种群
    [Chrom ObjV] =reins(Chrom, SelCh,1, 1, ObjV, ObjVSel);       
    %代计数器增加
    gen=gen+1;       
    
    %保存最优值
    trace(1, gen)=min(ObjV);       
    trace(2, gen)=mean(ObjV);  
    
    % 记录最佳值
    if gen==1
        Val1=PVal;
        Val2=P;
        MinVal=min(ObjV);%最小时间
        STemp=S;
    end
    %记录 最小的工序
    if MinVal> trace(1,gen)
        Val1=PVal;
        Val2=P;
        MinVal=trace(1,gen);
        STemp=S;
    end
    
end

% 当前最佳值
PVal=Val1; %工序时间
P=Val2;  %工序 
S=STemp; %调度基因含机器基因

%% 描绘解的变化
figure(1)
plot(trace(1,:));
hold on;
plot(trace(2,:),'-.');grid;
legend('解的变化','种群均值的变化');

%% 显示最优解
figure(2);
MP=S(1,PNumber*MNumber+1:PNumber*MNumber*2);
for i=1:WNumber  
    val= P(1,i);
    a=(mod(val,100)); %工序
    b=((val-a)/100); %工件
    Temp=Jm{b,a};
    mText=Temp(MP(1,i));
    
    x1=PVal(1,i);
    x2=PVal(2,i);
    
    y1=mText-1;
    y2=mText;
    plotRec(x1,x2,mText);
    
    plotRec(PVal(1,i),PVal(2,i),mText);
    hold on;
    
    fill([x1,x2,x2,x1],[y1,y1,y2,y2],[1-1/b,1/b,b/PNumber]);
    text((x1+x2)/2,mText-0.25,num2str(P(i)));
end

仿真结果

采用多层编码遗传算法求解车间调度问题，共有6个工件，在10台机器上加工，每个工件都要经过6道加工工序，每个工序可选择机器序号所列。
工具可选机器列表

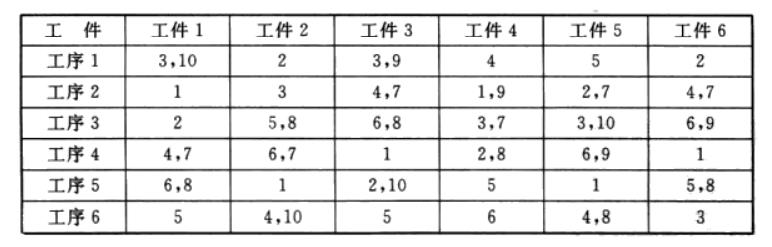
工序加工时间

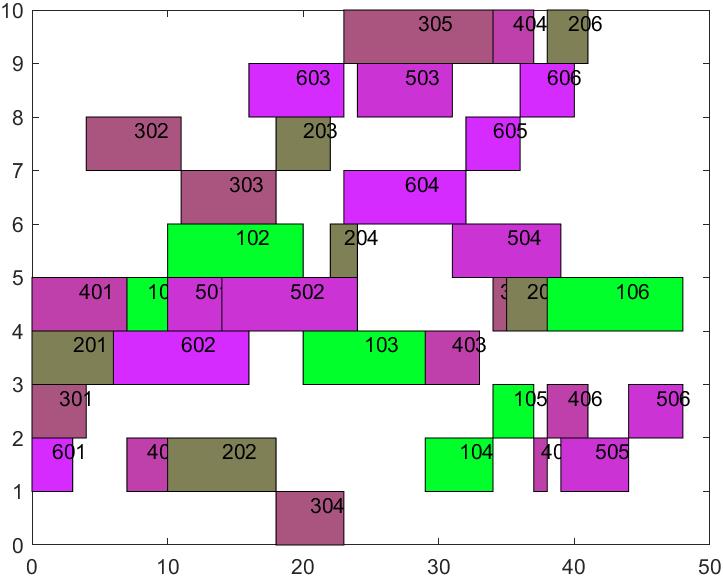
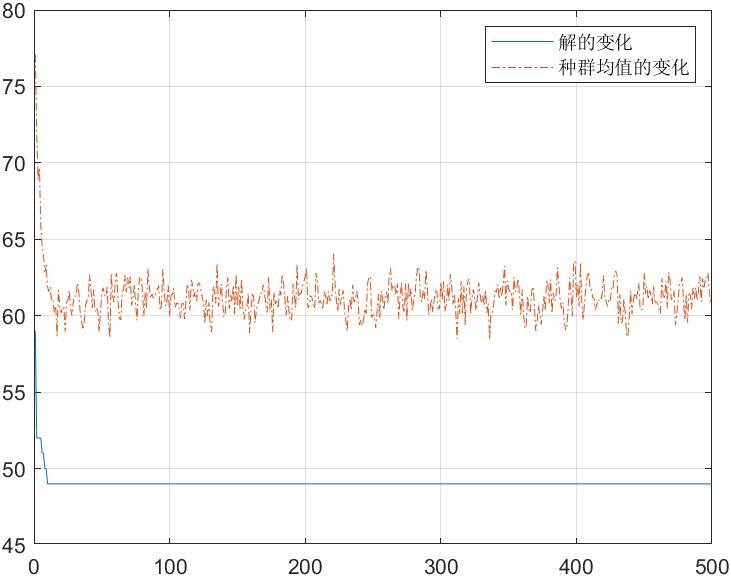
算法的基本参数为：种群数目为40，最大迭代次数为50，交又概率为0.8，变异概率为0.6，算法搜索得到的全部工件完成的最短时间为47s，算法搜索过程如图所示。

下载链接