图计算软件NetworkX和Graphscope有啥差别?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图计算软件NetworkX和Graphscope有啥差别?相关的知识,希望对你有一定的参考价值。
近年来,全球大数据进入加速发展时期,数据量呈现指数级爆发式增长,而这些大量数据中不同个体间交互产生的数据以图的形式表现,如何高效地处理这些图数据成为了业界及其关心的问题。很过用普通关系数据无法跑出来的结果,用图数据进行关联分析会显得异常高效。提到处理图数据,我们首先想到NetworkX,这是网络计算上常用的Python包,可提供灵活的图构建、分析功能。但是我们使用NetworkX跑大规模图数据时,不仅经常碰到内存不足的问题,而且分析速度很慢,究其原因,是NetworkX只支持单机运行。通过网上搜索,新发现了一个名为GraphScope的系统不仅号称兼容NetworkX的API,而且支持分布式部署运行,性能更优。针对GraphScope和NetworkX的处理能力,我们参考图计算中常用的测试框架LDBC,通过一组实验来对比下二者的性能。
一、实验介绍
为了比较两者的计算效率,先用阿里云拉起了配置为8核CPU,32GB内存的四台ECS,设计了三组比较实验,分别是NetworkX单机下的计算性能,GraphScope单机多worker的计算性能以及GraphScope分布式多机多worer的计算性能。
数据上,我们选取了SNAP开源的图数据集twitter,来自 LDBC数据集的datagen-7_5-fb,datagen-7_7-zf和datagen-8_0-fb作为实验数据,以下是数据集的基本信息:
· Twitter: 81,307个顶点,1,768,135条边
· Datagen-7_5-fb: 633,432个顶点,34,185,747条边,稠密图
· Datagen-7_7-zf: 13,180,508个顶点,32,791,267条边,稀疏图
· Datagen-8_0-fb: 1,706,561个顶点,107,507,376条边,这个数据集主要测试两个系统可处理的图规模能力
实验设计上我选择常用的SSSP、BFS、PageRank、WCC算法,以及较高复杂度的All Pair shortest Path length算法,以载图时间,内存占用和计算时间这三个指标为依据,对两个系统进行计算性能的比较。
NetworkX是一个单机系统,在实验中只考虑NetworkX在单机环境下的运行时间;GraphScope支持分布式运行,故进行两个配置,一个是单机4worker,另外一个配置是4台机器,每台机器4个worker。
二、实验结果
首先,GraphScope的载图速度比NetworkX显著提升。
在前三个图数据集中,无论是GraphScope的单机多worker模式,还是GraphScope的分布式模式,载图速度都比NetworkX快:
GraphScope单机模式载图速度平均比NetworkX快5倍,最高纪录——在datagen-7_5-fb上比NetworkX快了6倍。
分布式模式下GraphScope的载图时间比NetworkX平均快了27倍,最高纪录——在datagen-7_7-zf数据集上比NetworkX快了63倍。
在datagen-8_0-fb数据集上,NetworkX因内存溢出无法载图,GraphScope单机多worker和GraphScope分布式载图时间分别为142秒和13.6秒。
————————————————
版权声明:本文为CSDN博主「6979阿强」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/tanekf6979/article/details/120067176 参考技术A NetworkX是单机系统,主要做图分析。GraphScope是由阿里巴巴达摩院智能计算实验室研发的图计算平台,是全球首个一站式超大规模分布式图计算平台,并且还入选了中 国科学技术协会“科创中 国”平台。Graphscope的代码在github.com/alibaba/graphscope上开源。本回答被提问者采纳 参考技术B 说到图计算,我们首先想到NetworkX,我们使用它跑大规模数据时,经常会碰到内存不足以及分析速度慢,因为Networkx只支持单机运行,而GraphScope不仅兼容NetworkX的API,而且支持分布式部署运行,性能更优。
图计算系统分为两个流派: general purpose和graph-specific代表图计算系统分别为GraphX和Gemini, GraphScope。在计算时间上,GraphScope和Gemini的计算效率远超GraphX。 参考技术C 说到图计算,我们首先想到NetworkX,我们使用它跑大规模数据时,经常会碰到内存不足以及分析速度慢,因为Networkx只支持单机运行,而GraphScope不仅兼容NetworkX的API,而且支持分布式部署运行,性能更优。
图计算系统分为两个流派: general purpose和graph-specific代表图计算系统分别为GraphX和Gemini, GraphScope。在计算时间上,GraphScope和Gemini的计算效率远超GraphX。行业内著名的图计算框架包括NetworkX、GraphX、CuGraph和GraphScope等。
GraphScope 是阿里巴巴达摩院智能计算实验室研发并开源的,依托于阿里海量数据和丰富场景,是全球首个一站式超大规模分布式图计算平台。 参考技术D 11月9日,阿里巴巴宣布将开源一站式超大规模分布式图计算平台GraphScope。GraphScope项目组告诉DeepTech,12月将开源1.0版本,希望在易编程、高性能和一站式三个方面,解决全球图计算领域主要研发瓶颈。
阿里巴巴以自有超大规模商业场景,和达摩院智能计算研究为基础,自研了交互式图查询引擎、高性能图分析引擎和图深度学习引擎及相关开发者生态工具和集成。各个引擎的核心能力由GraphScope整合。
同日,中国科协、中国科学院、中国工程院主办的世界科技与发展论坛上,GraphScope被列为重要科技发布之一。正在进行的双11中,以GraphScope为底层框架的图计算网络,也正在搜索推荐、智能风控等核心场景发挥作用。
今年疫情期间,基于GraphScope的大规模因果图推理,还帮助自动识别和预测了影响航线价格浮动及机场中转变化的关键因素,克服了传统深度学习的黑盒缺点,让AI知其然、更知其所以然。
GraphScope项目总负责人、阿里巴巴集团资深副总裁周靖人认为,图结构数据是各种实体关联关系的一种自然表达,只有高效理解这些实体概念之间的广泛联系,才能让数字智能技术进一步赋能实体产业。
图计算仍然面临三大挑战
1735年瑞士数学家莱昂哈德·欧拉面对的柯尼斯堡七桥问题,可能是最早的图计算命题。而现代图计算问题则复杂数千倍,图计算性能近年来已经进步的数10倍,但仍然存在三个大规模应用挑战:一是相关领域问题复杂,计算模式多样,大量解决方案碎片化;二是学习难度大,对于非专业编程人士门槛很高;三是跨域数据量大、计算效率仍然偏低。
传统的机器学习计算框架在解决时间序列数据、非结构化数据(如视频)已经比较高效。但对于相对比较稀疏、高维度的关联数据,则需要图计算性能、架构和平台的持续进步。
若把中国484.65万公里的公路组成一个巨大的迷宫,运用GraphScope可在一毫秒内跑完所有的岔路。
“GraphScope提供了一站式的友好的编程环境 ,它不仅支持多种核心的图计算范式和它们之间高效的数据交换,提供了面向Python接口的单机抽象,从而屏蔽了大规模分布式计算的系统复杂性。”阿里巴巴资深专家、GraphScope团队成员钱正平告诉DeepTech。
通俗来说,图是一个由点和边构成的数学模型,能够非常容易地表达实体和数据之间的复杂关联。与阿里巴巴诸多技术开源项目类似,GraphScope来源于阿里巴巴集团内丰富的图场景与真实应用对于大规模图计算提出的需求。比如电商的知识图谱构建、风险控制、阿里云网络安全、商品的搜索推荐和广告等。正在进行的双11中,图计算也在商品推荐、智能物流和网络安全等方面发挥着重要作用。
“图模型可以很自然表达这些领域中数据间的复杂关联与结构特征。利用这些特征往往可以增强大数据分析的效果,为用户提供更精准和可靠的信息。”钱正平告诉DeepTech。
三大引擎支撑GraphScope
DeepTech独家获得资料显示,GraphScope开源项目的核心引擎主要有三驾马车:实时交互式图查询引擎、高性能图分析引擎、可扩展的图深度学习引擎。
1)交互式图查询引擎:实时图计算赋能行业革新
“深入理解图数据”是在多样化场景中有效利用图计算,挖掘深层洞察和创造新数据价值的必要前提。为此,商业用户及领域专家往往需要在交互式环境中,高效的探索和展现图数据。
GraphScope利用了高层声明式图查询语言—Gremlin,让领域专家和非计算机专业用户都可以简洁的表达复杂图遍历模式。同时,还提供了“业界第一个自动并行化Gremlin执行引擎”,让大规模、分布式环境中对图的复杂遍历所涉及的内存管理与动态策略优化等系统难题得以向用户隐藏。
GraphScope能够降低使用门槛,促使图计算人人可用,这方面具体体现在能够促进与更多行业领域专家的深度合作,让他们能够其领域知识跟图计算本身系统能力结合起来,在更多行业实现技术革新。
钱正平告诉DeepTech:“在海量数据的计算上,相比已有图上的交互式分析工具,我们希望GraphScope能提供至少一个数量级的性能(即查询延时)优势,让很多大规模的应用从不可能变成可能,而这种性能的量变能够触发业务效果的质变。”
2)高性能图分析引擎:让大规模图计算人人可用
除了交互式的图计算场景,图分析也是大数据图计算的重要一环。现实世界中的各种实体间关系、线上线下的各种交互场景,如社交媒体网络,化学结构,蛋白质相互作用网络、知识图谱、交通网络、通信网络、供应链与交易网络等,都广泛用到了大规模图分析。
GraphScope团队研发了一个基于不动点计算的大规模分布式图计算引擎。它扩展自局部计算-增量计算的不动点计算理论。在分布式环境中,各计算节点在初始轮根据自身持有的数据进行局部计算,之后通过几轮信息交换,每一轮都将来自别的计算节点信息作为更新,触发增量计算,一直到系统稳定时计算结束。该过程经过严谨的理论证明,保证在前提条件满足下,该分析引擎具有终止性和准确性。
该引擎支持了阿里巴巴内部20多种业务,相对原有方案体现了十分显著的性能提升效果,在一些业务上获得2-3个数量级的性能提升。此外,该分析引擎还支撑了双十一智能风控、新春五福红包发放等重点场景,经受了海量数据和瞬时峰值的实战考验。
3)高性能、可扩展的图深度学习
图引擎的应用已经延伸到了人工智能领域,融合了图计算和深度学习的图神经网络(GNN)更是成为了当下AI领域中非常热门的子领域,被研究者给予了很高的期待。图结构可以表达人类知识体系和现实生产生活中的复杂关系,从而在一切皆向量的深度学习中融入了知识和结构,使得深度学习由感知学习迈向认知学习。
GNN算法从开发到工业化落地,仍然处在快速发展和迭代的阶段。应用场景的拓宽、算法理论的变化、编程范式的变化都可能带来平台的变化甚至颠覆。
GraphScope通过整合上述三个核心组件,提供了一站式图计算的处理能力。同时,GraphScope通过生态丰富、语义灵活的Python编程接口,将多样化的图操作无缝集成。通过开发者本地的一个Python脚本,就可以实现对集群中海量图数据的Gremlin交互查询、图分析算法调用和进行图神经网络训练等等。此外,GraphScope还利用阿里已经开源的Vineyard项目,实现了上述操作之间高效的全内存中间结果数据交换,进一度提高应用流水线端到端的效率。
在世界科技与发展论坛上,阿里巴巴认为,随着GraphScope开源多个提升智能技术底层能力的突破,未来可对标以TensorFlow和Hadoop为代表的人工智能底层计算架构,助益全球数字经济加快发展。
钱正平预计,“GraphScope与TensorFlow等框架,在系统上会有一个协同关系,即将深度学习和传统的图模型做更紧密的结合,取得更好的效果。”
NetworkX:Python图与网络模型基础
在《运筹学》课堂上,我们学习过图与网络,当时用到R语言下的igraph包来计算和展示结果。Python下也有类似甚至更好的库: NetworkX。
安装命令如下
conda install networkx
引入约定为
import networkx as nx
1 图的绘制
无向图
无向图由点和边构成,其绘制思路为:①新建空图→②添加点→③添加边。
新建空的无向图
G = nx.Graph()
以后所有的信息都添加在无向图G上。
添加点:addnode和add_nodes_from
# 添加一个点
G.add_node(1) # 点的名字叫1
G.add_node('a') # 点的名字叫a
# 添加一组点
G.add_nodes_from([2,3,4])
虽然还没有讲到怎么展示这张图,但你可能想看看自己已经画了啥;所以我们剧透一下:输入nx.draw(G)看看吧。
添加边:add_edge和add_edges_from
# 添加一条边
G.add_edge(1,2) # 在1、2之间添加边
G.add_edge(1,'a') # 在1、a之间添加边
# 添加一组边
G.add_edges_from([(2,3),(3,4,),('a',3)])
# 添加边时自动生成点
G.add_edge(3,'b') # 此前没有添加过b点
# 添加圈
G.add_cycle(['b','c','d'])
# 注意这些命令都有color参数,将来会用到
移除点或边使用remove_*系列方法。
展示图
NetworkX可以结合matpltlib库来展示图,因此需要载入plt:
import matplotlib.pyplot as plt
最常用的展示命令是 networkx.draw(),所有参数都是可选的。
nx.draw()
简单介绍一些可选参数,如
ax:画纸名
nodecolor/edgecolor/font_color:点、边、字颜色
nodeshape/nodesize:点的形状和大小
style:边的形状(solid/dashed/dotted/dashdot)
alpha:点和边的透明度
with_labels:点是否显示标签
arrows/arrowstyle/arrowsize:有向图的箭头设定
我们并列展示默认和自定义结果:
fig = plt.figure(figsize=(20,5))
ax1 = plt.subplot(121)
nx.draw(G,ax=ax1)
ax2 = plt.subplot(122)
nx.draw(G,ax=ax2,node_color='pink',with_labels=True,node_size=500,node_shape='D',style='-.')
plt.draw()
另有 networkx.draw_networkx()函数,支持自定义点的位置(类型)。
有向图
有向图和无向图的差别仅仅在边是有方向的:
新建空的有向图
G = nx.DiGraph() # 注意差别
添加点:略
添加有向边
G.add_edge(1,2)
G.add_edges_from([(2,3),(2,4),(3,4),(4,3)])
nx.draw(G,ax=ax2,node_color='pink',with_labels=True,arrowstyle='fancy',edge_color='pink')
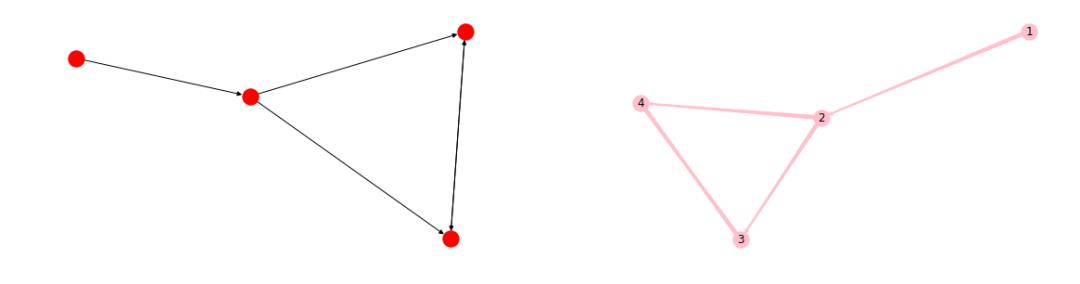
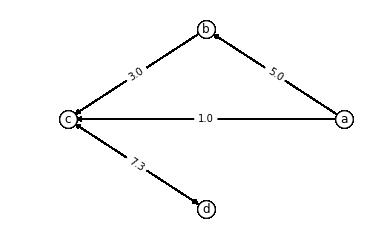
2 从图到网络:权的添加
方法一
add_weighted_edges_from方法能够接受(起点,终点,权重)作为元素的序列。推荐这种方法。
G = nx.DiGraph()
elist = [('a', 'b', 5.0), ('b', 'c', 3.0), ('a', 'c', 1.0), ('c', 'd', 7.3)]
G.add_weighted_edges_from(elist)
方法二
add_edge方法可以添加weight参数。
G.add_edge(1,2,weight=5.5)
方法三
类索引方法,在修改权重时非常有用。
G[1][2]['weight']=5.5
G.edges[1,2]['weight']=5.5
添加权重标签
按照上述三个方法添加的边权重,将被记录在边属性下,我们可以通过G.edges(data=True)方法来查看:
G.edges(data=True)
特别注意参数data一定要为True,不指定data参数时默认只提取边的起点和终点。结果如下:
OutEdgeDataView([('a', 'b', {'weight': 5.0}), ('a', 'c', {'weight': 1.0}), ('b', 'c', {'weight': 3.0}), ('c', 'd', {'weight': 7.3})])
关系已经很明确了,我们用元组u,v,w来解包,并将其放在键为边,值为权的字典中:
# 方法一:for循环
label = {}
for (u,v,d) in G.edges(data=True):
label[(u,v)] = str(d['weight'])
# 方法二:字典推导式
label = {(u,v):str(d['weight']) for u,v,d in G.edges(data=True)}
绘制权重标签
我们分4步来画图:点→边→点标签→边标签(顺序不重要)。因为要分4个图层来画,所以需要明确点的位置,不能用nx.draw()这种随性的方法。
首先定义点的位置pos:
pos = nx.spring_layout(G)
这表明我们使用Fruchterman-Reingold的力引导算法来画图,目的是减少边的交叉(推荐)。可选的pos还有circular_layout、kamada_kawai_layout、random_layout、rescale_layout、shell_layout和spectral_layout,点少的时候看不出来,点多就不一样了。
nx.draw_networkx_nodes(G,pos)
nx.draw_networkx_labels(G,pos)
nx.draw_networkx_edges(G,pos)
nx.draw_networkx_edge_labels(G, pos, label) # 关注这里
plt.axis('off') # 不显示坐标
plt.draw()
默认的标签是放在边的中间,可以用label_pos调节,这对双箭头的有向边很重要。
3 最短路
《运筹学》课程中,我们学习了Dijkstra算法;NetworkX提供了相应的命令:
dijkstra_predecessor_and_distance:给出某起点到所有点的最短路径和最短路程,结果也包含两部分,可以用元组解包提取;
dijkstra_path:给出从某起点到某终点的最短路径;
dijkstra_path_length:给出从某起点到某终点的最短路程。
构造一个有向图
G = nx.DiGraph()
elist = [(1,2,3),(1,3,2),(1,4,5),
(2,6,7),
(3,4,1),
(4,6,5),
(5,3,5),(5,4,3),(5,6,1)]
G.add_weighted_edges_from(elist)
求点1到点6的最短路。
展示这个有向图
pos = nx.circular_layout(G)
label = {(u,v):str(d['weight']) for u,v,d in G.edges(data=True)}
nx.draw_networkx_nodes(G,pos,node_color='w',edgecolors='k')
nx.draw_networkx_nodes(G,pos,node_color='pink',edgecolors='k',nodelist=[1,6])
nx.draw_networkx_labels(G,pos,font_color='k')
nx.draw_networkx_edges(G,pos)
nx.draw_networkx_edge_labels(G, pos,label,label_pos=0.3)
plt.axis('off')
plt.draw()
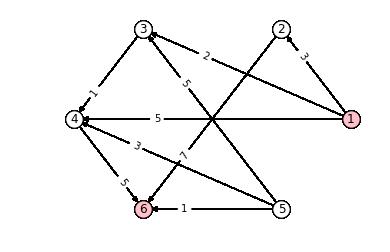
Dijkstra算法求最短路
指定起点,不指定终点
pred, dist = nx.dijkstra_predecessor_and_distance(G,1)
print('到每个点的最短路的上一个点:',pred)
print('到每个点的最短路的路程:',dist)
结果:
到每个点的最短路的上一个点: {1: [], 2: [1], 3: [1], 4: [3], 6: [4]}
到每个点的最短路的路程: {1: 0, 3: 2, 2: 3, 4: 3, 6: 8}
指定起点和终点
path = nx.dijkstra_path(G,1,6)
length = nx.dijkstra_path_length(G,1,6)
print('从点1到点6的最短路径是',path)
print('从点1到点6的最短路程是',length)
将最短路径画出来:
附代码:
pos = nx.circular_layout(G)
label = {(u,v):str(d['weight']) for u,v,d in G.edges(data=True)}
nx.draw_networkx_nodes(G,pos,node_color='w',edgecolors='k')
nx.draw_networkx_nodes(G,pos,node_color='pink',edgecolors='k',nodelist=[1,6])
nx.draw_networkx_labels(G,pos,font_color='k')
nx.draw_networkx_edges(G,pos)
el = [(path[i],path[i+1]) for i in range(len(path)-1)]
nx.draw_networkx_edges(G,pos,edge_color='r',edgelist=el)
nx.draw_networkx_edge_labels(G, pos,label,label_pos=0.3)
plt.axis('off')
plt.draw()
4 最大流
掌握了最短路再来看最大流,就是很简单的事情了。
通过capacity参数为边添加最大容量;
使用
maximum_flow函数求解。
构造包含最大容量的有向图
elist = [(1,2,6),(1,4,6),(2,3,2),(2,5,3),(3,5,2),(3,6,2),(4,3,3),
(4,6,1),(4,7,2),(5,7,5),(6,7,4)]
G = nx.DiGraph()
for u,v,c in elist:
G.add_edge(u,v,capacity=c)
绘制这个图
pos = nx.circular_layout(G)
label = {(u,v):str(d['capacity']) for u,v,d in G.edges(data=True)}
# 或者label = {(u,v):str(c) for u,v,c in elist}
nx.draw_networkx_nodes(G,pos,node_color='w',edgecolors='k')
nx.draw_networkx_nodes(G,pos,node_color='pink',edgecolors='k',nodelist=[1,7])
nx.draw_networkx_labels(G,pos,font_color='k')
nx.draw_networkx_edges(G,pos)
nx.draw_networkx_edge_labels(G, pos,label,label_pos=0.5)
plt.axis('off')
plt.draw()
图中边的标签表示最大容量(而非单位运价)。我们想求得从点1到点7的最大流。
计算最大流
flow_value, flow_dict = nx.maximum_flow(G, 1, 7)
通过提取flow_value,我们可以知道从点1到点7的最大流为10;
通过提取flow_dict,我们可以知道最大流情形下,每条边的实际流量:
{1: {2: 5, 4: 5},
2: {3: 2, 5: 3},
3: {5: 2, 6: 2},
4: {3: 2, 6: 1, 7: 2},
5: {7: 5},
6: {7: 3},
7: {}}
我们也可以通过 flow_dict[<起点>][<终点>]来确定特定边上的实际容量,如 flow_dict[1][4]表示边(1,4)上的实际流量为5。
5 结语
NetworkX是复杂网络计算库,能做的事情远不止最短路和最大流。手册在这里,进步靠自己:
https://networkx.github.io/documentation/stable/_downloads/networkx_reference.pdf
以上是关于图计算软件NetworkX和Graphscope有啥差别?的主要内容,如果未能解决你的问题,请参考以下文章