数据结构线段树笔记2

Posted 2022-02-05 karshey

【数据结构】零基础线段树笔记1

参考和引用：
线段树讲解 本博客主要是这个的笔记。

线段树相关知识

线段树的结构

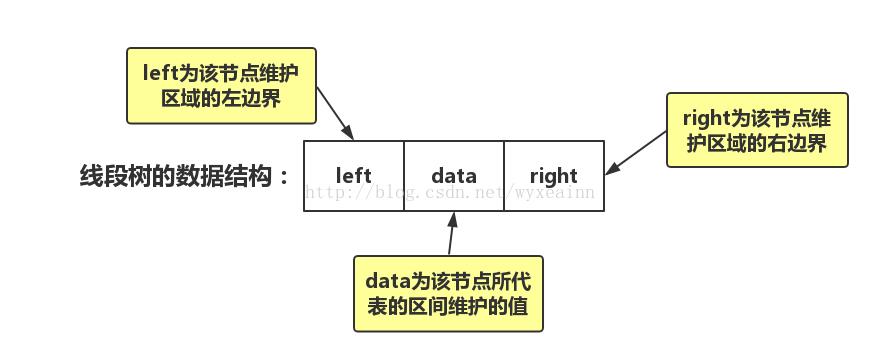
N的原数组，要4N的大小去存储线段树
原因：看线段树讲解吧。

代码相关

更新当前节点 push_up

是更新当前节点的操作。
有两种写法：

1. 如果是维护区间最大值，则区间的最大值是max(左区间.maxn,右区间.maxn)；
2. 如果是维护区间和值，则直接加和

//维护区间最大值
void push_up1(int root)

	nodes[root].maxn=max(nodes[root<<1].maxn,nodes[root<<1|1].maxn);
 

//维护区间的和值
void push_up2(int root) 

	nodes[root].maxn=nodes[root<<1].maxn+nodes[root<<1|1].maxn;

线段树的构建

//构建线段树
void build(int root,int left,int right)

	nodes[root].left=left;
	nodes[root].right=right;
	if(left==right)
	
		nodes[root].maxn=num[left];//叶子结点的值就是原数组的值本身 
		return;
	
	
	int mid=(left+right)>>1;
	
	build(root<<1,left,mid); //root<<1可以写作root*2 
	build(root<<1|1,mid+1,right); //root<<1之后一定是个偶数，所以|1就一定会+1 也可以写作root*2+1
	 
	push_up(root);//更新当前节点的函数 

单点更新，区间查询

单点更新：

//单点更新
void update(int pos,int val,int root)//把原数组中pos位置的值改为val

	//是叶子节点
	if(nodes[root].left==nodes[root].right)
	
		nodes[root].data=val;
		return;
	 
	 
	int mid=(left+right)>>1;
	if(pos<=mid) update(pos,val,root<<1);//在左区间更新 
	else update(pos,val,root<<1|1);//在右区间更新 
	 
	push_up(root);

下推标记：

//下推标记
void push_down(int root)

	//有标记则需要更新
	if(nodes[root].lazy>0)
	
		//获得左右区间的长度 
		int leftlen=nodes[root<<1].right-nodes[root<<1].left+1;
		int rightlen=nodes[root<<1|1].right-nodes[root<<1|1].left+1;
		
		//更新左右区间和值 
		nodes[root<<1].data+=leftlen*nodes[root].lazy;
		nodes[root<<1|1].data+=rightlen*nodes[root].lazy; 
		
		//下推标记
		nodes[root<<1].lazy+=nodes[root].lazy;
		nodes[root<<1|1].lazy+=nodes[root].lazy;
		
		//root的标记推完了 变为0
		nodes[root].lazy=0; 
	  
 

区间查询：

//区间查询
int query(int l,int r,int root)

	if(l<=nodes[root].left&&nodes[root].right<=r)// l left right r 要找的lr已经找到了一部分 
	
		return node[root].data;
	
	
	push_down(root);
	
	int mid=(nodes[root].left+nodes[root].right)/2;
	int ans=0;
	
	if(l<=mid) ans+=query(l,r,root<<1);
	if(r>mid) ans+=query(l,r,root<<1|1);
	
	return ans;
 

区间更新

//区间更新：将[l,r]中的数字都加上add
void update(int l,int r,int add,int root)

	//找到了 
	if(l<=nodes[root].left&&nodes[root].right<=r)
	
		nodes[root].data+=(nodes[root].right-nodes[root].left+1)*add;
		nodes[root].lazy+=add;
		return;
	
	push_down(root);//下推标记
	
	int mid=(nodes[root].right+nodes[root].left)/2;
	if(l<=mid) update(l,r,add,root<<1);
	if(r>mid) update(l,r,add,root<<1|1);
	push_up(root);
 

区间求和

//区间求和
int query(int root,int start,int end,int l,int r)

	if(start>r||end<l)
	
		return 0;
	
	
	else if(l<=start&&end<=r)
	
		return node[root].data;
	
	
	else
	
		int mid=(start+end)/2;
		
		int left_sum=query(root<<1,start,mid,l,r);
		int right_sum=query(root<<1|1,mid+1,end,l,r);
		
		return left_sum+right_sum;
	
  

剩下还有区间合并等，下次一定