数据结构与算法之寻找两个正序数组的中位数的求解思路和算法示例

Posted 2022-02-05 Serendipity·y

一、题目要求

• 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2，请找出并返回这两个正序数组的中位数 。
• 算法的时间复杂度应该为 O(log (m+n)) 。
• 示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

• 示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

• 示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

• 示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

• 示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

• 提示：
• • nums1.length == m
• • nums2.length == n
• • 0 <= m <= 1000
• • 0 <= n <= 1000
• • 1 <= m + n <= 2000
• • -106 <= nums1[i], nums2[i] <= 106

二、求解算法

① 解法一

• 简单粗暴，先将两个数组合并，两个有序数组的合并也是归并排序中的一部分。
• 然后根据奇数，还是偶数，返回中位数。
• Java 示例：

public double findMedianSortedArrays(int[] nums1, int[] nums2) 
    int[] nums;
    int m = nums1.length;
    int n = nums2.length;
    nums = new int[m + n];
    if (m == 0) 
        if (n % 2 == 0) 
            return (nums2[n / 2 - 1] + nums2[n / 2]) / 2.0;
         else 
            return nums2[n / 2];
        
    
    if (n == 0) 
        if (m % 2 == 0) 
            return (nums1[m / 2 - 1] + nums1[m / 2]) / 2.0;
         else 
            return nums1[m / 2];
        
    

    int count = 0;
    int i = 0, j = 0;
    while (count != (m + n)) 
        if (i == m) 
            while (j != n) 
                nums[count++] = nums2[j++];
            
            break;
        
        if (j == n) 
            while (i != m) 
                nums[count++] = nums1[i++];
            
            break;
        

        if (nums1[i] < nums2[j]) 
            nums[count++] = nums1[i++];
         else 
            nums[count++] = nums2[j++];
        
    

    if (count % 2 == 0) 
        return (nums[count / 2 - 1] + nums[count / 2]) / 2.0;
     else 
        return nums[count / 2];
    

② 解法二

• 其实，不需要将两个数组真的合并，只需要找到中位数在哪里就可以了。
• 开始的思路是写一个循环，然后里边判断是否到了中位数的位置，到了就返回结果，但这里对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后，出了 for 循环对边界的判断也会分几种情况。
• 首先是怎么将奇数和偶数的情况合并一下，用 len 表示合并后数组的长度，如果是奇数，我们需要知道第 （len+1）/2 个数就可以了，如果遍历的话需要遍历 int(len/2 ) + 1 次。如果是偶数，我们需要知道第 len/2和 len/2+1 个数，也是需要遍历 len/2+1 次。所以遍历的话，奇数和偶数都是 len/2+1 次。
• 返回中位数的话，奇数需要最后一次遍历的结果就可以了，偶数需要最后一次和上一次遍历的结果。所以用两个变量 left 和 right，right 保存当前循环的结果，在每次循环前将 right 的值赋给 left。这样在最后一次循环的时候，left 将得到 right 的值，也就是上一次循环的结果，接下来 right 更新为最后一次的结果。
• 循环中该怎么写，什么时候 A 数组后移，什么时候 B 数组后移，用 aStart 和 bStart 分别表示当前指向 A 数组和 B 数组的位置，如果 aStart 还没有到最后并且此时 A 位置的数字小于 B 位置的数组，那么就可以后移了，也就是aStart＜m&&A[aStart]< B[bStart]。
• 但如果 B 数组此刻已经没有数字了，继续取数字 B[ bStart ]，则会越界，所以判断下 bStart 是否大于数组长度了，这样 || 后边的就不会执行了，也就不会导致错误了，所以增加为 aStart＜m&&(bStart) >= n||A[aStart]<B[bStart]) 。
• Java 示例：

public double findMedianSortedArrays(int[] A, int[] B) 
    int m = A.length;
    int n = B.length;
    int len = m + n;
    int left = -1, right = -1;
    int aStart = 0, bStart = 0;
    for (int i = 0; i <= len / 2; i++) 
        left = right;
        if (aStart < m && (bStart >= n || A[aStart] < B[bStart])) 
            right = A[aStart++];
         else 
            right = B[bStart++];
        
    
    if ((len & 1) == 0)
        return (left + right) / 2.0;
    else
        return right;

③ 解法三

• 上边的两种思路，时间复杂度都达不到题目的要求 O(log(m+n)。看到 log，很明显，只有用到二分的方法才能达到，不妨用另一种思路，题目是求中位数，其实就是求第 k 小数的一种特殊情况，而求第 k 小数有一种算法。
• 解法二中，我们一次遍历就相当于去掉不可能是中位数的一个值，也就是一个一个排除。由于数列是有序的，其实完全可以一半儿一半儿的排除，假设要找第 k 小数，可以每次循环排除掉 k/2 个数。
• 假设要找第 7 小的数字：

• 比较两个数组的第 k/2 个数字，如果 k 是奇数，向下取整，也就是比较第 3 个数字，上边数组中的4 和下边数组中的 3，如果哪个小，就表明该数组的前 k/2 个数字都不是第 k 小数字，所以可以排除。也就是 1，2，3 这三个数字不可能是第 7 小的数字，可以把它排除掉。将 1349 和 45678910 两个数组作为新的数组进行比较。
• 更一般的情况 A[1] ，A[2] ，A[3]，A[k/2] … ，B[1]，B[2]，B[3]，B[k/2] … ，如果 A[k/2]<B[k/2] ，那么A[1]，A[2]，A[3]，A[k/2] 都不可能是第 k 小的数字。
• A 数组中比 A[k/2] 小的数有 k/2-1 个，B 数组中，B[k/2] 比 A[k/2] 小，假设 B[k/2] 前边的数字都比 A[k/2] 小，也只有 k/2-1 个，所以比 A[k/2] 小的数字最多有 k/1-1+k/2-1=k-2个，所以 A[k/2] 最多是第 k-1 小的数。而比 A[k/2] 小的数更不可能是第 k 小的数了，所以可以把它们排除。
• 橙色的部分表示已经去掉的数字：

• 由于已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4，此时两个数组，比较第 2 个数字，3 < 5，所以可以把小的那个数组中的 1 ，3 排除掉了：

• 我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4，怎么办呢？由于两个数相等，所以无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，就假设 4 > 4 吧，所以此时将下边的 4 去掉：

• 由于又去掉 1 个数字，此时要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4，所以第 7 小的数字是 4。
• 每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候：

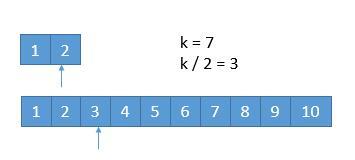
• 此时 k / 2 等于 3，而上边的数组长度是 2，此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3，所以就会导致上边的数组 1，2 都被排除，造成下边的情况：

• 由于 2 个元素被排除，所以此时 k = 5，又由于上边的数组已经空了，只需要返回下边的数组的第 5 个数字就可以了。
• 从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。
• 所以采用递归的思路，为了防止数组长度小于 k/2，所以每次比较 min(k/2，len(数组) 对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且 k 要减去排除的数字的个数，递归出口就是当 k=1 或者其中一个数字长度是 0 了。
• Java 示例：

public double findMedianSortedArrays(int[] nums1, int[] nums2) 
        int n = nums1.length;
        int m = nums2.length;
        // 因为数组是从索引0开始的，因此我们在这里必须+1，即索引(k+1)的数，才是第k个数。
        int left = (n + m + 1) / 2;
        int right = (n + m + 2) / 2;
        // 将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k
        return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
    
    private int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) 
        // 因为索引和算数不同6-0=6，但是是有7个数的，因为end初始就是数组长度-1构成的。
        // 最后len代表当前数组(也可能是经过递归排除后的数组)，符合当前条件的元素的个数
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        // 让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1
        // 就是如果len1长度小于len2，把getKth()中参数互换位置，即原来的len2就变成了len1，即len1，永远比len2小
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        // 如果一个数组中没有了元素，那么即从剩余数组nums2的其实start2开始加k再-1.
        // 因为k代表个数，而不是索引，那么从nums2后再找k个数，那个就是start2 + k-1索引处就行了。因为还包含nums2[start2]也是一个数。因为它在上次迭代时并没有被排除
        if (len1 == 0) return nums2[start2 + k - 1];

        // 如果k=1，表明最接近中位数了，即两个数组中start索引处，谁的值小，中位数就是谁(start索引之前表示经过迭代已经被排出的不合格的元素，即数组没被抛弃的逻辑上的范围是nums[start]--->nums[end])。
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);

        // 为了防止数组长度小于 k/2,每次比较都会从当前数组所生长度和k/2作比较，取其中的小的(如果取大的，数组就会越界)
        // 然后素组如果len1小于k / 2，表示数组经过下一次遍历就会到末尾，然后后面就会在那个剩余的数组中寻找中位数
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        // 如果nums1[i] > nums2[j]，表示nums2数组中包含j索引，之前的元素，逻辑上全部淘汰，即下次从J+1开始。
        // 而k则变为k - (j - start2 + 1)，即减去逻辑上排出的元素的个数(要加1，因为索引相减，相对于实际排除的时要少一个的)
        if (nums1[i] > nums2[j]) 
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
         else 
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));