LeetCode精选TOP面试题（中等2）

Posted 2022-02-04 _light_house_

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode精选TOP面试题（中等2）相关的知识，希望对你有一定的参考价值。

文章目录

787. K 站中转内最便宜的航班

（bellman-ford最短路）

本题是一个用限制条件的最短路径问题，我们可以使用bellman-ford算法直接计算即可。

本质上bellman-ford算法就是一个dp。

dp[k][i]表示从起点出发最多经过k条边走到i中所有路径中长度的最小值。

所以f[k][i] = minf[k - 1][j] + dist[j]。

class Solution 
    static int INF = 0x3f3f3f3f;
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) 
        int[][] f = new int[k + 2][n];
        for (int i = 0; i < k + 2; i ++)
            Arrays.fill(f[i], INF);
        f[0][src] = 0;
        int ans = INF;
        for (int t = 1; t <= k + 1; t ++) 
            for (int[] flight : flights) 
                int from = flight[0], to = flight[1], w = flight[2];
                f[t][to] = Math.min(f[t][to], f[t - 1][from] + w);
            
         
        for (int t = 1; t <= k + 1; t ++)
            ans = Math.min(ans, f[t][dst]);
        return ans == INF ? -1 : ans;

（bellman-ford最短路-空间优化）

因为每一次只用到二维数组中的上一层中的数字，所以我们可以使用两个一维数组滚动的使用。

class Solution 
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) 
        int INF = 0x3f3f3f3f;
        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[src] = 0;
        // k个中间点,k+1条边,k+1次循环
        for (int i = 0; i <= k; i ++) 
            // 用cur表示临时数组
            int[] cur = new int[n];
            cur = Arrays.copyOf(dist, n);
            // 上面两句可以使用int[] cur = dist.clone();替代
            for (int[] f : flights) 
                int from = f[0], to = f[1], w = f[2];
                cur[to] = Math.min(cur[to], dist[from] + w);
            
            dist = cur;
        
        if (dist[dst] == INF) return -1;
        else return dist[dst];

Java的完整写法

class Solution 
    class Edge 
        int x, y, w;
        Edge(int _x, int _y, int _w) 
            x = _x; y = _y; w = _w;
        
    

    int N = 110, INF = 0x3f3f3f3f;
    // n个点，m条边，k步之内，从src到dst
    int n, m, k, src, dst;
    List<Edge> list = new ArrayList<>();
    int[] dist = new int[N];

    public int findCheapestPrice(int _n, int[][] flights, int _src, int _dst, int _k) 
        n = _n; src = _src; dst = _dst; k = _k + 1;
        for (int[] f : flights) 
            list.add(new Edge(f[0], f[1], f[2]));
        
        m = list.size();
        int ans = bellman_ford();
        return ans > INF / 2 ? -1 : ans;
    

    public int bellman_ford() 
        Arrays.fill(dist, INF);
        dist[src] = 0;
        for (int i = 0; i < k; i ++) 
            int[] cur = dist.clone();
            for (Edge e : list) 
                int x = e.x, y = e.y, w = e.w;
                dist[y] = Math.min(dist[y], cur[x] + w);
            
        
        return dist[dst];

319. 灯泡开关

（数学+脑筋急转弯）

如果一个灯泡最后是亮的，说明它被摁了偶数次。如果灯泡最后是灭的，说明它被摁了奇数次。而一个灯泡被摁的次数和n的约数个数有关。如果一个数字是完全平方数说明它的约数个数为奇数。如果一个数字不是完全平方数，说明它的约数个数一定是偶数。所以我们只要看1~n中有多少的完全平方数即可。即sqrt(n)。

class Solution 
    public int bulbSwitch(int n) 
        return (int)Math.sqrt(n);

743. 网络延迟时间

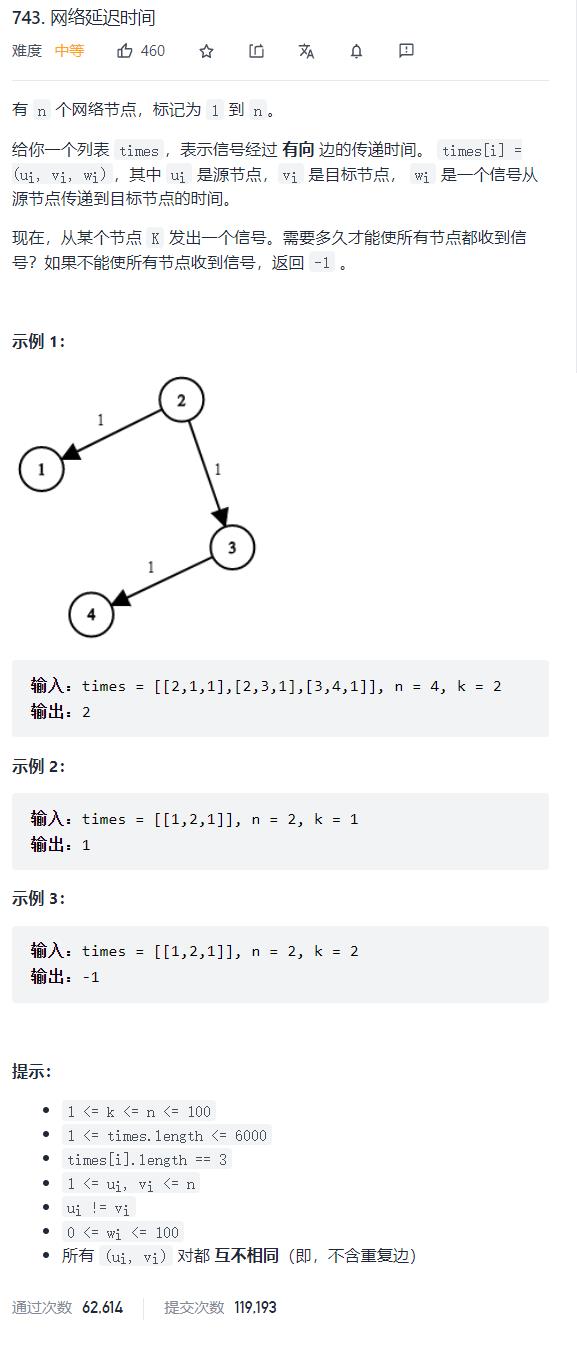
我们要知道多久才可以使得所有的点都可以接收到信号。其实就是在求从k出发到达所有点的最短路中，哪一个最短路需要的时间最多。（因为如果最大的最短路所用的时间一定可以到达其他所有的点）。

所以本题主要考察我们最短路的图论模板怎么写，有5种方式的图论最短路朴素版Dijkstra，堆优化版Dijkstra，bellman-ford，spfa和floyd最短路。

（朴素版Dijkstra最短路）

每一次确定一个离源点最近的点，然后用这个点去优化从这个出发的路径。

class Solution 
    final int INF = 0x3f3f3f3f;
    public int networkDelayTime(int[][] times, int n, int k) 
        int[][] g = new int[n + 1][n + 1];
        for (int i = 1; i <= n; i ++)
            Arrays.fill(g[i], INF);
        for (int[] time : times) 
            int a = time[0], b = time[1], w = time[2];
            g[a][b] = w;
        
        int[] dist = new int[n + 1];
        Arrays.fill(dist, INF);
        dist[k] = 0;
        
        boolean[] vis = new boolean[n + 1];
        for (int i = 1; i <= n; i ++) 
            int x = -1;
            for (int y = 1; y <= n; y ++) 
                if (!vis[y] && (x == -1 || dist[x] > dist[y]))
                    x = y;
            vis[x] = true;
            for (int j = 1; j <= n; j ++)
                dist[j] = Math.min(dist[j], dist[x] + g[x][j]);
        
        int ans = 0;
        for (int i = 1; i <= n; i ++) 
            ans = Math.max(ans, dist[i]);
        
        return ans > INF / 2 ? -1 : ans;

（堆优化版Dijkstra最短路）

我们可以使用堆的结构优化上面使用循环找到离源点最近的一个点的位置。使用priority_queue，并且存放从该点到源点的距离, 该点的编号，就可以在O(1)的时间内找到距离源点最近的点。

class Solution 
    final int N = 110, M = 6010;
    int INF = 0x3f3f3f3f;
    int[] he = new int[N], e = new int[M], w = new int[M], ne = new int[M];
    int idx = 0;
    void add(int a, int b, int c) 
        e[idx] = b;
        w[idx] = c;
        ne[idx] = he[a];
        he[a] = idx;
        idx ++;
    
    boolean[] vis = new boolean[N];
    int[] dist = new int[N];
    int n, k;
    public int networkDelayTime(int[][] times, int _n, int _k) 
        n = _n; k = _k;
        Arrays.fill(he, -1);
        Arrays.fill(dist, INF);
        for (int[] time : times) 
            int a = time[0], b = time[1], c = time[2];
            add(a, b, c);
        
        dijkstra();
        int ans = 0;
        for (int i = 1; i <= n; i ++) 
            ans = Math.max(ans, dist[i]);
        
        return ans > INF / 2 ? -1 : ans;
    
    void dijkstra() 
        dist[k] = 0;
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b)->a[0]-b[0]);
        q.add(new int[]0, k);
        while (!q.isEmpty()) 
            int[] top = q.poll();
            int ver = top[1], distance = top[0以上是关于LeetCode精选TOP面试题（中等2）的主要内容，如果未能解决你的问题，请参考以下文章 
 图解精选 TOP 面试题 001 | LeetCode 237. 删除链表中的节点
 leetcode 最常见的 150 道前端面试题（简单题上）
 leetcode 最常见的150道前端面试题（简单题下）
 ⭐算法入门⭐《二分枚举》中等02 —— LeetCode 面试题 10.09. 排序矩阵查找
 ⭐算法入门⭐《堆》中等01 —— LeetCode 面试题 17.09. 第 k 个数
 精选力扣500题 第42题 LeetCode 155. 最小栈c++/java详细题解