数学题目

Posted 2023-05-08

　　对于十来岁的孩子，正是思维敏捷，精力充沛，记忆效果好的时候，多做一些有趣的数学题目，对于学习和成长非常的有益。你知道有哪些有趣的数学 智力题 吗？下面是我给你精心整理的16道有趣的数学智力题，快跟我一起来看看这些题你能做出多少题吧! 　　16道有趣的数学智力题推荐 　　有趣数学智力题1 　　有两根不均匀分布的香，香烧完的时间是一个小时，你能用什么 方法 来确定一段15分钟的时间? 　　有趣数学智力题2 　　一个经理有三个女儿，三个女儿的年龄加起来等于13，三个女儿的年龄乘起来等于经理自己的年龄，有一个下属已知道经理的年龄，但仍不能确定经理三个女儿的年龄，这时经理说只有一个女儿的头发是黑的，然后这个下属就知道了经理三个女儿的年龄。请问三个女儿的年龄分别是多少?为什么? 　　有趣数学智力题3 　　有三个人去住旅馆，住三间房，每一间房$10元，于是他们一共付给老板$30，第二天，老板觉得三间房只需要$25元就够了于是叫小弟退回$5给三位客人，谁知小弟贪心,只退回每人$1，自己偷偷拿了$2，这样一来便等于那三位客人每人各花了九元，于是三个人一共花了$27，再加上小弟独吞了$2，总共是$29。可是当初他们三个人一共付出$30那么还有$1呢? 　　有趣数学智力题4 　　有两位盲人，他们都各自买了两对黑袜和两对白袜，八对袜了的布质、大小完全相同，而每对袜了都有一张商标纸连着。两位盲人不小心将八对袜了混在一起。他们每人怎样才能取回黑袜和白袜各两对呢? 　　有趣数学智力题5 　　有一辆火车以每小时15公里的速度离开洛杉矶直奔纽约，另一辆火车以每小时20公里的速度从纽约开往洛杉矶。如果有一只鸟，以30公里每小时的速度和两辆火车同时启动，从洛杉矶出发，碰到另一辆车后返回，依次在两辆火车来回飞行，直到两辆火车相遇，请问，这只小鸟飞行了多长距离? 　　有趣数学智力题6 　　你有两个罐子，50个红色弹球，50个蓝色弹球，随机选出一个罐子，随机选取出一个弹球放入罐子，怎么给红色弹球最大的选中机会?在你的计划中，得到红球的准确几率是多少? 　　有趣数学智力题7 　　你有四个装药丸的罐子，每个药丸都有一定的重量，被污染的药丸是没被污染的重量+1.只称量一次，如何判断哪个罐子的药被污染了? 　　有趣数学智力题8 　　你有一桶果冻，其中有黄色，绿色，红色三种，闭上眼睛，抓取两个同种颜色的果冻。抓取多少个就可以确定你肯定有两个同一颜色的果冻? 　　有趣数学智力题9 　　对一批编号为1～100，全部开关朝上(开)的灯进行以下操作：凡是1的倍数反方向拨一次开关;2的倍数反方向又拨一次开关;3的倍数反方向又拨一次开关……问：最后为关熄状态的灯的编号? 　　有趣数学智力题10 　　想象你在镜子前，请问，为什么镜子中的影像可以颠倒左右，却不能颠倒上下? 　　有趣数学智力题11 　　两个圆环，半径分别是1和2，小圆在大圆内部绕大圆圆周一周，问小圆自身转了几周?如果在大圆的外部，小圆自身转几周呢? 　　有趣数学智力题12 　　假如每3个空啤酒瓶可以换一瓶啤酒，某人买了10瓶啤酒，那么他最多可以喝到多少瓶啤酒? 　　有趣数学智力题13 　　一群人开舞会，每人头上都戴着一顶帽子。帽子只有黑白两种，黑的至少有一顶。每个人都能看到 其它 人帽子的颜色，却看不到自己的。主持人先让大家 看看别人头上戴的是什幺帽子，然后关灯，如果有人认为自己戴的是黑帽子，就打自己一个耳光。第一次关灯，没有声音。于是再开灯，大家再看一遍，关灯时仍然 鸦雀无声。一直到第三次关灯，才有劈劈啪啪打耳光的声音响起。问有多少人戴着黑帽子? 　　有趣数学智力题14 　　有十袋苹果，每袋十个，且其中的任何一个苹果均等重;已知其中有九袋里的苹果均重50克，只有一袋中的为45克。现只有杆称一支，要求只称一次，就将其中是45克的那一袋苹果给找出来，问如何称量? 　　有趣数学智力题15 　　一个两位数，十位上的数字与个位上的数字之和是10，如果把这两个数字的位置 交换，所得到的数就比原数小36，原来的两位数是( )。 　　有趣数学智力题16 　　把 蛋糕 切成相等的两块 　　有一个长方形蛋糕，切掉了长方形的一块(大小和位置随意)，你怎样才能直直的一刀下去，将剩下的蛋糕切成大小相等的两块? 　　你想知道这16道数学智力题的答案吗?请往下拉☟☟☟查看智力题答案 　　16道数学智力题答案 　　1.香a点燃一头，香b点燃两头。等香b烧完时，时间过去了30分钟。再把香a剩下的另一头也点燃。从这时起到a烧完的时间就是15分钟。 　　2.三女的年龄应该是2、2、9。因为只有一个孩子黑头发，即只有她长大了，其他两个还是幼年时期即小于3岁，头发为淡色。再结合经理的年龄应该至少大于25。 　　3.典型的偷换概念。事实上3人只付出了27元，老板得了25元，小弟拿了2元。 　　4.将每对袜子拆开一人一只。 　　5.设洛杉矶到纽约的铁路长为A公里。则两辆火车到相遇用了A/(15+20)小时，也就是小鸟飞行的时间。所以小鸟飞行的距离就是速度×时间=30×A/35=6/7的洛杉矶到纽约的铁路长。 　　6.1/2的几率。先选出球在选罐子。这样罐子其实对球的颜色无影响。 　　7.1号罐取1丸，2号罐取2丸，3号罐取3丸，4号罐取4丸，称量该10个药丸，比正常重量重几就是几号罐的药有问题。 　　8.4个。数量>颜色种类。颜色必重复。 　　9.有10盏灯为灭，分别为1、4、9、16、25、36、49、64、81、100号。因为：每个质数能被1和自身整除，所以质数的灯是亮的。设一个合 数能被N个数整除，N必然是个偶数。对于非某数平方的合数来说，将被开关N次也就是偶数次，灯保留为亮;对于上面列出的平方数，则只被开关N-1次，所以灯是灭的。 　　10.镜像对称的轴是人的中轴 　　11.无论内外，小圆转两圈。 　　12.喝完10瓶后用9个空瓶换来3瓶啤酒(喝完后有4个空瓶) 喝完这三瓶又可以换到1瓶啤酒(喝完后有2个空瓶)这时他有2个空酒瓶，如果他能向老板先借一个空酒瓶，就凑够了3个空瓶可以换到一瓶啤酒，把这瓶喝完后将空瓶还给老板就可以了。　所以他最多可以喝10+3+1+1=15瓶 　　13.有三个人戴黑帽。假设有N个人戴黑，当N=1时，戴黑人看见别人都为白则能肯定自己为黑。于是第一次关灯就应该有声。可以断定N>1。对于每 个戴黑的人来说，他能看见N-1顶黑帽，并由此假定自己为白。但等待N-1次还没有人打自己以后，每个戴黑人都能知道自己也是黑的了。所以第N次关灯就有 N个人打自己。 　　14.首先将十袋苹果编号为1、2。。。。10，并在各袋中拿出与编号相同的苹果，称一次，如果是50的倍数，那就是十号袋，否则，差一个5克就是9号袋，差二个就是8号袋。 　　15.一个两位数，交换个位和十位上数字得到一个新两位数，原数与新数的差一定是9的倍数，用这个差除以9就是个位与十位的数字差(大减小).这里是36÷9=4，说明原数个位数字与十位数字的差是4(大减小)，而它们和是10，于是问题变成和差问题.原数是73. 　　16.将完整的蛋糕的中心与被切掉的那块蛋糕的中心连成一条线。这个方法也适用于立方体。请注意，切掉的那块蛋糕的大小和位置是随意的，不要一心想着自己切生日蛋糕的方式，要跳出这个圈子。 数学智力题相关推荐： 1. 数学智力题大全 2. 小学数学智力题及答案 3. 数学智力题大全及答案 4. 趣味数学智力题之画龙点睛详解 5. 吃有关的小学生数学智力题 6. 智力数学趣味题及答案集锦 参考技术A 1.有一批图书总数在1000本以内，若按24本书一捆，最后一捆差2本；若按28本书一捆，最后一捆还是差2本书；若按32本一捆，最后一捆是30本。这批图书有多少本？请以上的题详细解答，

如果加上二本,则正好.
24,28,32的最小公倍数是672

672<1000,所以,共有图书是672-2=670本.

有一批图书，总数在1000本以内。若按24本书包成一捆，最后一捆差2本；若按28本书包成一捆，最后一捆还是差2本；若按32本包一捆，最后一捆是30本。这批图书有多少本？
解：“若按32本包一捆，最后一捆是30本。”这句话的意思是说：若按32本包一捆，最后一捆仍旧差2本。这道题是让我们求24、28、32的最小公倍数，再把求出来的数减2：[24，28，32]＝672，672－2＝670（本）
答：这批图书有670本。

2. 一个书架分上中下三层，一共放书384本。如果从上层取出与中层一样多的本数放入中层，再从中层取出与下层一样多的本数放入下层，最后从下层取出与上层现在一样多的本数放入上层，这时三层书架中的书相等。书架的中层原来有多少本书？

现在上中下三层都有：384÷3=128本

下层未给上层,上层有:128÷2=64本,下层有:128+64=192本 中层有:128本

中层未给下层,下层有:192÷2=96本,中层有:128+96=224本 上层有:64本

上层未给中层,中层有:224÷2=112本,上层有:64+112=176本 下层有:96本

书架的中层原来有:112本

4.
1。各取5盒放天平上，若一样重则在剩下的5盒中，若不一样重则在轻的那5盒中
2，各取2盒放天平上，若一样重则在剩下那一盒中，若不一样重则在轻的那2盒中。
3.用天平称出最后那两盒中轻的那盒。
所以最少3次

5.
1÷(1-1/4-2/3)说明，第一个1是指小宁，其中的1/4和2/3是不包括小宁在内的，括号里的1是一个整体。整体-去前后的人数就是等于小宁自己。=1÷1/12小宁自己就占了1/12=12(人)总人数是12小宁站的这一排至少有12人

6.
4/15,7/15,14/15

7.240=60X4这两个自然数是4，60或12，20

8.x/4+3=x/5+4

移向 合并同类项

x/20=1

所以x=20

9.80-55=25 说明有25只大兔子，25-10=15 说明有15只大灰兔， 63-15=48 灰兔-大灰兔=小灰兔，说明有48只小灰兔 参考技术B 当X=0时, 那么 a0=-2^5
令X=1 则（1-2）^5=a0+a1+a2+a3+a4+a5=-1 ①
a0=-2^5 ②
由①-②得a1+a2+a3+a4+a5=2^5-1
^5=a0+a1+a2+a3+a4+a5=-1 -a0=-2^5
则（-1-2）^5=a0-a1+a2-a3+a4-a5=-3^5 ③
由①-③得2（a1+a3+a5）=3^5-1
a1+a3+a5=（3^5-1）/2 参考技术C 现在小学生的题目都出这种的吗？？？
太难了，连产品成本都不给

NEFU离散2020年离散数学大作业/历年题目

【NEFU离散】2020年离散数学大作业

找19lxy学长借的账号，这些题大部分可以在学校OJ直接找到对应题目的，你们点击链接即可。
考虑到各位可能不怎么会C++，所以离散作业使用纯C语言进行解题.

题目

大多数是根据离散数学的公式来写程序，如果你知道基础公式的话就比较简单。但是OJ上写程序难度可能比锐格上大，因为没法套数据吧呵呵。如果你没玩过林大oj建议熟悉熟悉。
比赛在OJ比赛第四页

后面题目OJ上开了历年题目可以直接进去交

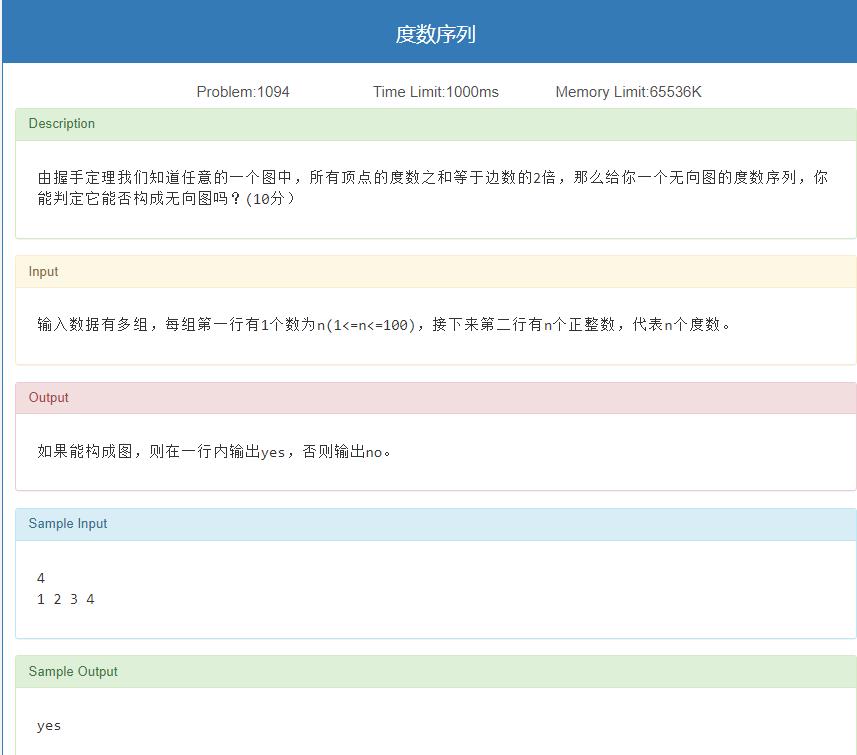
度数序列

题目链接

思路
可以看一下书本P135的例6.3
根据握手定理：所有顶点度数之和为边数两倍。
那么有推论，奇度顶点的个数一定是偶数的。
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int n;
	while(~scanf("%d",&n)){
		int cnt=0;
		for(int i=1,x;i<=n;i++){
			scanf("%d",&x);
			if(x&1)cnt++;
		}
		if(cnt&1)puts("no");
		else puts("yes");
	}
	return 0;
}

平面图

题目链接

思路
书本P159定理6.16
设G为任意的连通的平面图，则n-m+r=2。其中n为顶点数，m为边数，r为面数满足
$n-m+r=2$
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int n,r;
	while(~scanf("%d%d",&n,&r)){
		printf("%d\\n",n+r-2);
	}
	return 0;
}

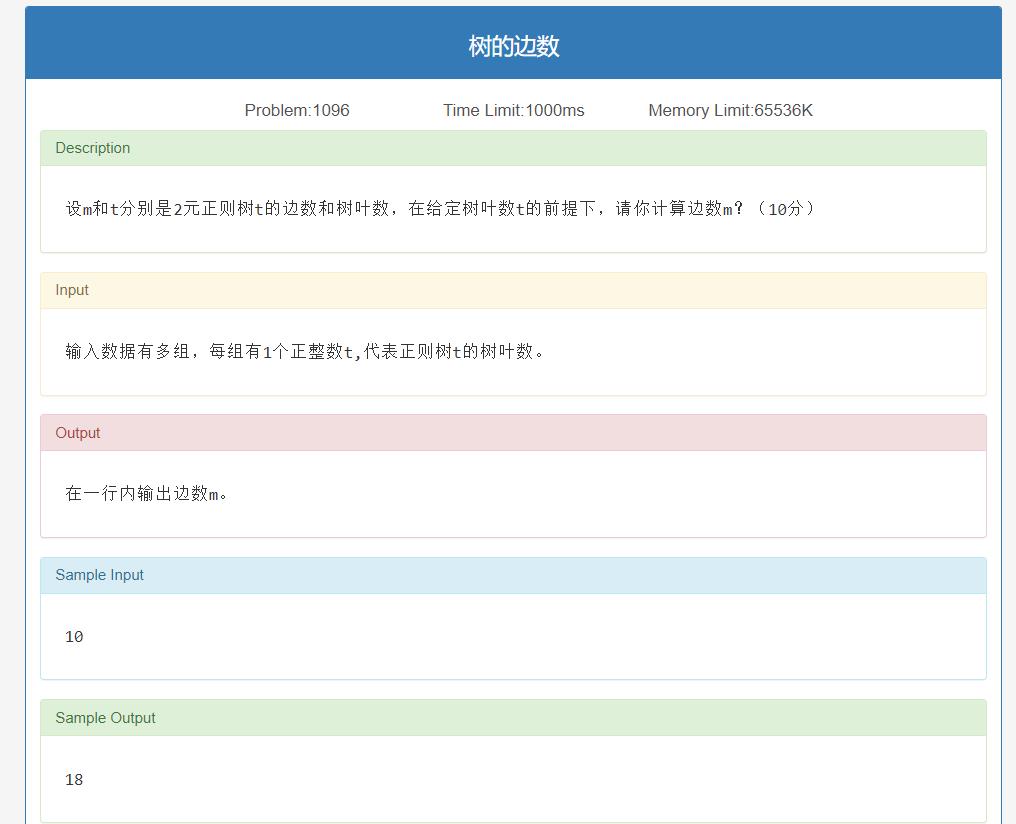
树的边数

题目链接

思路
2元正则树：T的每个分支点恰有2个儿子
其实想想最特殊的情况，2元完全正则树嘛（可以先看后面的一道题目）
可以发现$m=2(t-1)$

代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int t;
	while(~scanf("%d",&t)){
		printf("%d\\n",2*(t-1));
	}
	return 0;
}

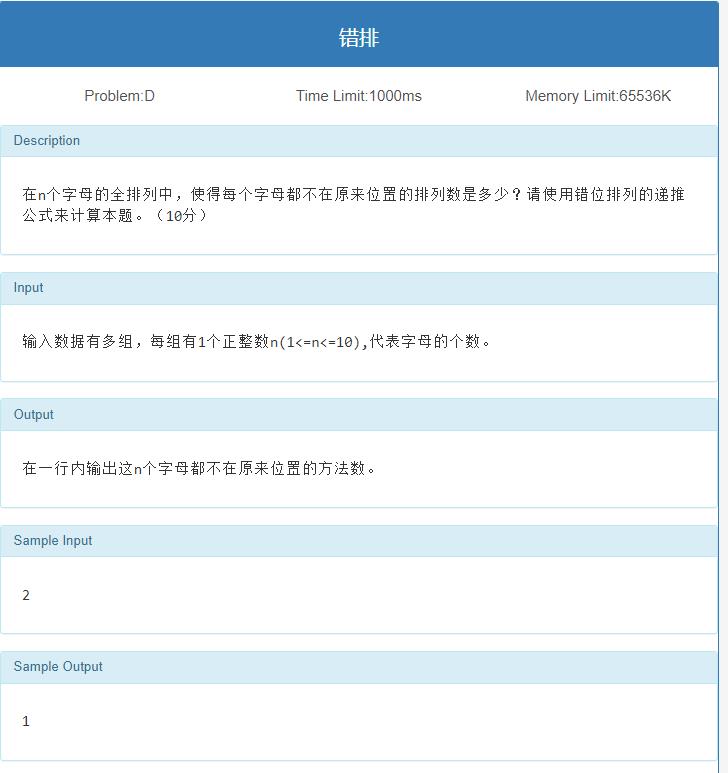
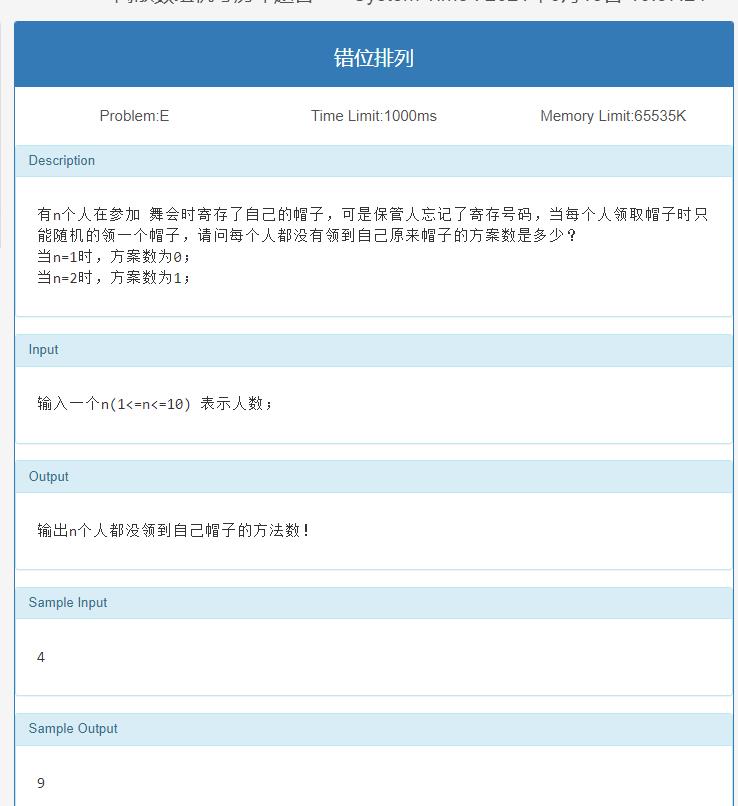
错排/错位排列

题目链接

思路
错排公式：要么用递推式，要么用近似值
代码
$D[n]=(int)(\frac{n!}{e}+0.5)$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define e 2.718281828459
int main(){
	int n;
	while(~scanf("%d",&n)){
		int fac=1;
		for(int i=1;i<=n;i++)fac*=i;
		int ans=(int)(fac/e+0.5);
		printf("%d\\n",ans);
	}
	return 0;
}

$D[n]=(n-1)(D[n-2]+D[n-1])$
$D[1]=0,D[2]=1$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int D[15];
int main(){
	int n;
	D[1]=0,D[2]=1;
	for(int i=3;i<=10;i++)D[i]=(i-1)*(D[i-1]+D[i-2]);
	while(~scanf("%d",&n)){
		printf("%d\\n",D[n]);
	}
	return 0;
}

数字编码

题目链接

思路
书上P218例10.3
代码
递推
$a[n]=6\ast a[n-1]+8^{n-1}$
$a[1]=7$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int a[15];
int main(){
	int n;
	a[1]=7;
	for(int i=2;i<=10;i++)a[i]=6*a[i-1]+pow(8,i-1);
	while(~scanf("%d",&n)){
		printf("%d\\n",a[n]);
	}
	return 0;
}

非递推式
$a[n]=\frac{6^n+8^n}{2}$
注意，如果用pow的话要转int，不然直接printf(%d)为输出0的

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main(){
	int n;
	while(~scanf("%d",&n)){
		printf("%d\\n",(int)(pow(6,n)+pow(8,n))/2);
	}
	return 0;
}

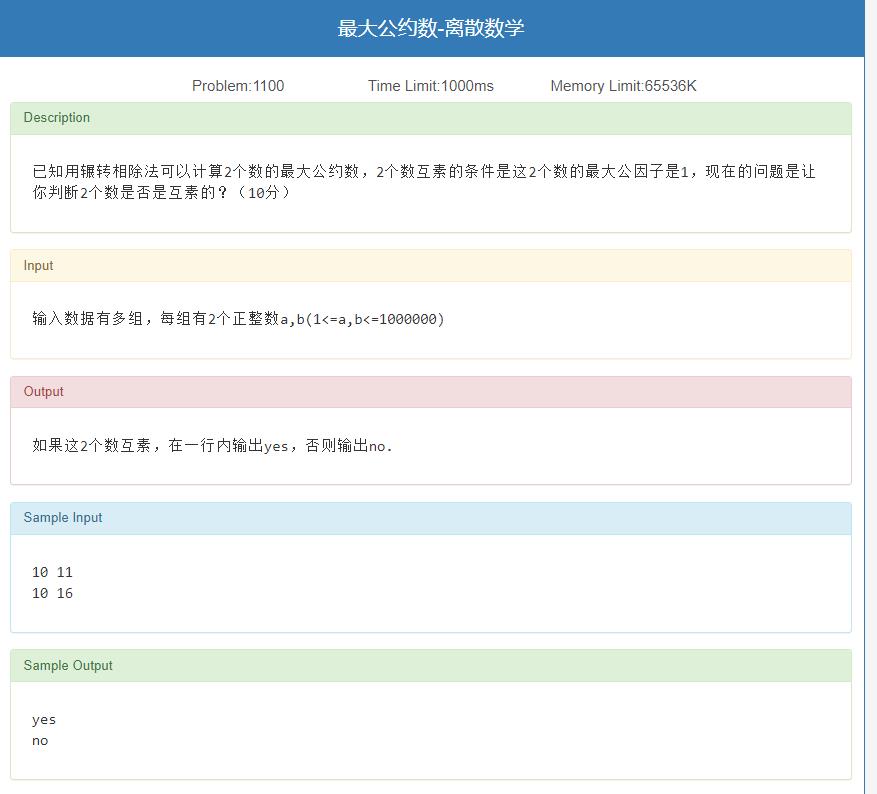
最大公约数-离散数学

题目链接

思路
x与y互素就是$gcd(x,y)=1$
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}
int main(){
	int x,y;
	while(~scanf("%d%d",&x,&y)){
		if(gcd(x,y)==1)puts("yes");
		else puts("no");
	}
	return 0;
}

接下来cy老师开始乱杀了呜呜呜
下面的题目去这个比赛里面做

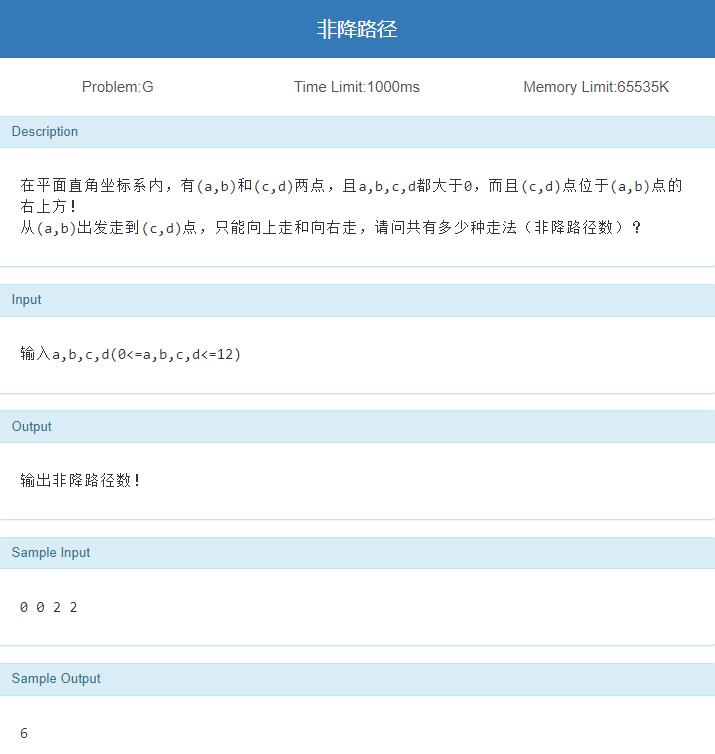
非降路径

题目链接（没开放）

思路
反手一个走迷宫DP统计方案数呵呵（如果你开心的话）
好吧，还是直接用书上P199公式吧
$ans=C_{c-a+d-b}^{c-a}$
本质是求组合数，数据非常友好，但是你直接阶乘会溢出的，所以我们求组合数要用递推式

代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int C[30][30];
int main(){

	for(int i=0;i<=24;i++)
		for(int j=0;j<=i;j++)
			if(!j)C[i][j]=1;
			else C[i][j]=C[i-1][j-1]+C[i-1][j];
			
	int a,b,c,d;	
	scanf("%d%d%d%d",&a,&b,&c,&d);
	int m=c-a+d-b,n=c-a;
	printf("%d\\n",C[m][n]);
	return 0;
}

2元完全正则树

题目链接（没开放）

思路
P178概念题目啦
知道啥是2元完全正则树即可
概念拆分：
r元树：T的每个分支点至多有r个儿子
r元正则树：T的每个分支点恰好有r个儿子
r元完全正则树：T是r元正则树，且所有树叶的层数均为树高
树的层数：树根到任意一点的通路长度
树的高：最大层数

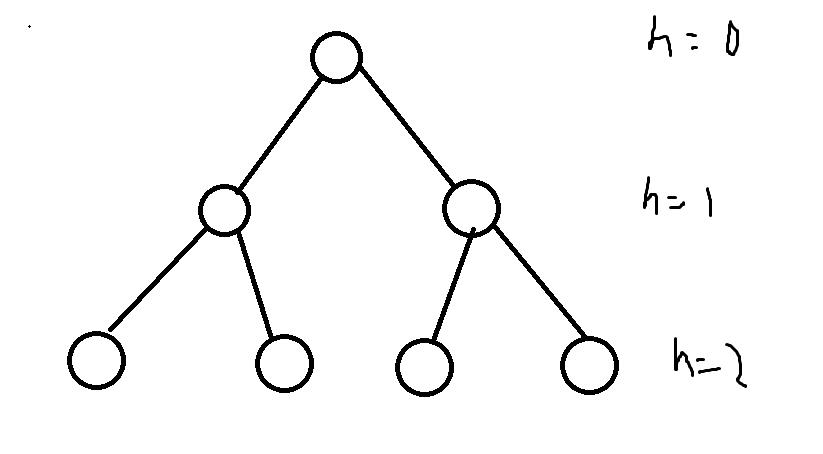
可以发现，对于树高为h的2元完全正则树
$顶点数=2^{h+1}-1$
$边数=0+2+4+8+16\dots \dots$
$树叶=2^h$

如果求2的次方，可以采用位移运算
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main(){
	int h;
	scanf("%d",&h);
	int edge=0;
	for(int i=1;i<=h;i++)edge+=1<<(i);
	printf("%d %d %d",(1<<(h+1))-1,edge,1<<h);
	return 0;
}

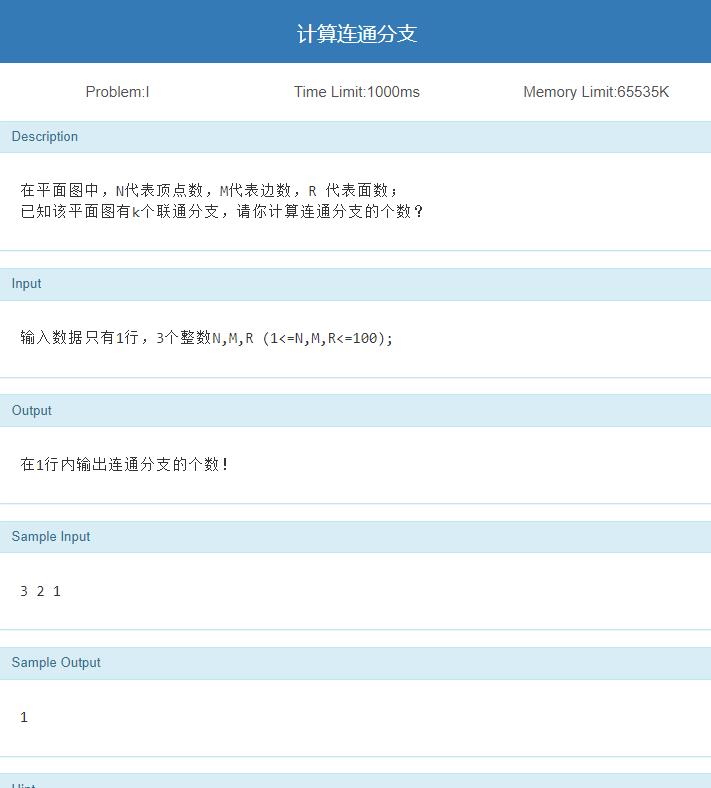
计算连通分支数

题目链接（未开放）

思路
书P159推论
G是具有k（k>=2）个连通分支的平面图，则 n − m + r = k + 1 n-m+r=k+1

以上是关于数学题目的主要内容，如果未能解决你的问题，请参考以下文章

数学中国数学建模网络挑战赛历年的题目和优秀论文哪里可以找到

语文课外知识、数学奥数题目

Python之数学题目练习

历年全国研究生数学建模竞赛(NPMCM)题目

哪些是二年级上册数学解决问题的题目

[数学] aw3725. 卖罐头(数学+推公式+思维)