十大经典排序算法

Posted 2022-02-01 Shoko0116

十大经典排序算法

• • LowB三人组
  • • 冒泡排序
    • 选择排序
    • 插入排序
  • NB三人组
  • • 快速排序
    • 堆排序
    • 归并排序
  • 其他排序
  • • 桶排序
    • 希尔排序
    • 计数排序
    • 基数排序

挨个移动位置的都是稳定排序，飞着排序的都是不稳定排序

LowB三人组

冒泡排序

# 冒泡排序
def bubble_sort(li):
     for i in range(len(li)-1): # 第i趟
          exchange = False
          for j in range(len(li)-i-1):
               if li[j] > li[j+1]: # 改成<则是降序排列
                    li[j], li[j+1] = li[j+1], li[j] # 交换位置
                    exchange = True
          ## print(li)
          if not exchange: # 判断是否已经排好序
               return

选择排序

选择排序需要创建一个新的列表，占内存

# 选择排序（优化版）
def select_sort(li):
     for i in range(len(li)-1): # 第i趟
          min_loc = i
          for j in range(i+1, len(li)):
               if li[j] < li[min_loc]:
                    min_loc = j
          li[i], li[min_loc] = li[min_loc], li[i]
          ## print(li)

插入排序

def insert_sort(li):
     for i in range(1, len(li)): # i表示摸到的牌的下标
          tmp = li[i]
          j = i - 1 # j表示手里的牌的下标
          while j >= 0 and li[j] > tmp:
               li[j+1] = li[j]
               j -= 1
          li[j+1] = tmp

NB三人组

快速排序

快速排序比冒泡排序快10倍，数越大差的越多

def partition(li, left, right):
     tmp = li[left]
     while left < right:
          while left < right and li[right] >= tmp: # 从右面找比tmp小的数
               right -= 1 # 往左走一步
          li[left] = li[right] # 把右边的值写到左边的空位上
          while left < right and li[left] <= tmp:
               left += 1
          li[right] = li[left] # 把左边的值写到右边的空位上 
     li[left] = tmp # 把tmp归为
     return left

def quick_sort(li, left, right):
     if left < right: # 至少两个元素
          mid = partition(li, left, right)
          quick_sort(li, left, mid-1)
          quick_sort(li, mid+1, right)

li = [5,7,3,6,4,1,2,9,8]
quick_sort(li, 0, len(li)-1)
print(li)

堆排序

根节点：A
叶子节点：不能分叉的节点 BC
树的深度：层数
树的度：看树里面谁分叉分的最多：6
孩子的节点/父节点：E叫做I的父节点
子树：拿出来的树


完全二叉树：最下一层可以不满，但是必须从左到右排序




如果是大根堆，堆顶永远都是最大的数
堆顶退休，从结尾最后一个数拿出一个数从新向下调整
这样每次出一个数，堆就在变小

退下的元素放在列表最后，但是标记

def sift(li, low, high): #调整函数
    """
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """
    i = low # i最开始指向根节点的的位置
    j = 2 * i + 1 # j开始是i的左孩子
    tmp = li[low] # 把堆顶存起来
    while j <= high: # 只要j位置有效
        if j + 1 <= high and li[j+1] > li[j]: # 右孩子存在，右孩子(j+1) > 左孩子(j)
            j = j + 1 # j指向右孩子
        if li[j] > tmp: # j > 堆顶元素 (此时j为孩子中较大的元素)
            li[i] = li[j] # j元素被提拔往上一层
            i = j # 往下看一层
            j = 2 * i + 1 # j跟着变化
        else:   # 堆顶元素 > 左孩子，把tmp放到i的位置上
            break
    li[i] = tmp # 把tmp放到叶子节点上

def heap_sort(li):
    # 开始建堆（构造堆）
    n = len(li)
    for i in range((n-2)//2, -1, -1): # 左闭右开，步长
        # i表示建堆的时候调整的那部分的根的下标
        sift(li, i, n-1) # 开始时i为n-1元素的父节点位置，n-1为最后的叶子节点
    # 建堆完成
    for i in range(n-1, -1, -1):
        # i指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i-1) # i-1是新的high

li = [i for i in range(100)]
import random
random.shuffle(li) # 打乱
print(li)
heap_sort(li)
print(li)

def sift(li, low, high): #调整函数
    """
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """
    i = low # i最开始指向根节点的的位置
    j = 2 * i + 1 # j开始是i的左孩子
    tmp = li[low] # 把堆顶存起来
    while j <= high: # 只要j位置有效
        if j + 1 <= high and li[j+1] < li[j]: # 右孩子存在，右孩子(j+1) > 左孩子(j)
            j = j + 1 # j指向右孩子
        if li[j] < tmp: # j > 堆顶元素 (此时j为孩子中较大的元素)
            li[i] = li[j] # j元素被提拔往上一层
            i = j # 往下看一层
            j = 2 * i + 1 # j跟着变化
        else:   # 堆顶元素 > 左孩子，把tmp放到i的位置上
            break
    li[i] = tmp # 把tmp放到叶子节点上

def topk(li,k):
    heap = li[0:k]
    for i in range((k-2)//2, -1, -1):
        sift(heap, i, k-1)
    # 1.建堆
    for i in range(k, len(li)-1):
        if li[i] > heap[0]:
            heap[0] = li[i]
            sift(heap, 0, k - 1)
    # 2.遍历
    for i in range(k-1, -1, -1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i - 1)
    # 3.出数
    return heap

import random
li = list(range(1000))
random.shuffle(li) # 打乱
print(topk(li, 10))

归并排序

def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high: #只要左右两边都有数
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    # while执行完，肯定有一部分没数了
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp

# li = [2, 4, 5, 7, 1, 3, 6, 8]
# merge(li, 0, 3, 7)
# print(li)

def merge_sort(li, low, high):
    if low < high: # 至少有两个元素，递归
        mid = (low + high) // 2
        merge_sort(li, low, mid) # 递归左边
        merge_sort(li, mid+1, high) # 递归右边
        merge(li, low, mid, high) # 将左边和右边合并

li = list(range(10))
import random
print(li)
merge_sort(li, 0, len(li)-1)
print(li)

其他排序

桶排序

0-99都放到0号桶里，100-199都放到9号桶里，…，9900-10000放到99号桶里，
注意10000不能放在100号桶里，不然会越界
桶号为0-99(n-1)
桶的空间是n*k

# 桶排序
def bucket_sort(li, n=100, max_num=10000):
    bucket = [[] for _ in range(n)] # 创建一个二维列表
    for var in li:
        i = min(var // (max_num // n), n-1) # i 表示var放到几号桶里，注意10000不能放在100号桶里，不然会越界
        bucket[i].append(var) # 把var放到i号桶里
        # 保持桶内的顺序，从后往前比较的冒泡排序
        for j in range(len(bucket[i])-1, 0, -1): # 从最后一个元素到第二个元素，注意后不包，取1
            if bucket[i][j] < bucket[i][j-1]:
                bucket[i][j], bucket[i][j-1] = bucket[i][j-1], bucket[i][j]
            else:
                break
    sorted_li = []
    for buc in bucket:
        sorted_li.extend(buc) # 将来自 iterable 的项添加到数组末尾,iterable 必须是一个数组
    return sorted_li



import random
li = [random.randint(0,100) for _ in range(100)]
print(li)
count_sort(li)
print(li)

希尔排序

希尔排序的时间复杂度比较复杂，并且和选取的gap有关

def insert_sort_gap(li, gap):
    for i in range(gap, len(li)):  # i表示摸到的牌的下标
        tmp = li[i]
        j = i - gap  # j表示手里的牌的下标
        while j >= 0 and li[j] > tmp: # 如果j有效且j > i元素，则交换位置
            li[j + gap] = li[j]
            j -= gap
        li[j + gap] = tmp #之后tmp就没用了

def shell_sort(li):
    d = len(li) // 2
    while d >= 1:
        insert_sort_gap(li, d)
        d //= 2

li = [3, 2, 4, 1, 5, 6, 8, 7, 9]
## li = [random.randint(0,10000) for i in range(100)] # 列表生成式
print(li)
shell_sort(li)
print(li)

计数排序

def count_sort(li, max_sort=100):
    count = [0 for _ in range(max_sort+1)]
    for val in li:
        count[val] += 1
    li.clear()
    for ind, val in enumerate(count):
        for i in range(val):
            li.append(ind)

import random
li = [random.randint(0,100) for _ in range(100)]
print(li)
count_sort(li)
print(li)

基数排序

按个位数分好桶

按个位数进行排序

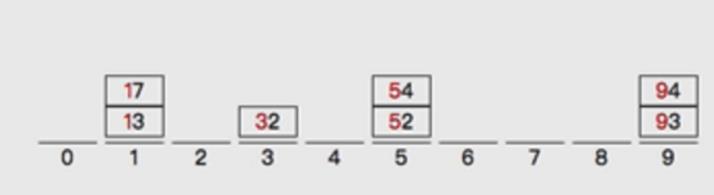
按十位数分好桶

按十位数进行排序

# 基数排序
def radix_sort(li):
    max_num = max(li) # 最大值 99->2,888->3,10000->5
    it = 0 # 迭代的次数
    while 10 ** it <= max_num: # 以888为例，10的三次方才大于888，所以it取3，对应888的位数；注意取=号的边界情况
        bucket = [[] for _ in range(10)] # 创建二维列表的桶
        # 开始分桶
        for var in li:
            # 987 it=1  987//10->98 98%10->8;   it=2 987//100->9 9%10=9
            digit = (var // 10 ** it) % 10
            bucket[digit].append(var)
        # 分桶完成
        li.clear()
        for buc in bucket:
            li.extend(buc)
        # 把桶重新写回li

        it += 1


import random
li = [random.randint(0,100) for _ in range(100)]
print(li)
radix_sort(li)
print(li)