stochastic matrices properties

Posted 2023-05-07

参考技术A 1 The question is actually easy if you write out all things Let x=(x_1
x_2
...
x_n)^T A= a_11
a_12
...a_1n a_21
a_22
...a_2n ... a_n1
a_n2
...a_nn where x_1+x_2+...+x_n=1 ; a_11+a_21+...+a_n1=1
a_1n+a_2n+...+a_nn=1 Ax= a_11x_1+a_12x_2+...+a_1nx_n a_21x_1+a_22x_2+...+a_2nx_n ... a_n1x_1+a_n2x_2+...+a_nnx_n Add them altogether (a_11x_1+a_12x_2+...+a_1nx_n)+(a_21x_1+a_22x_2+...+a_2nx_n)+...+(a_n1x_1+a_n2x_2+...+a_nnx_n) =(a_11+a_21+...+a_n1)x_1+(a_12+a_22+...+a_n2)x_2+...+(a_1n+a_2n+...+a_nn)x_n =x_1+x_2+...+x_n =1 2 The statement is wrong. I can let A and C are abitrary matrices an B is an diagonal matrix. Then A and B mute
B and C mute But generally
AC=CA is wrong 2009-02-01 19:21:37 补充： MR学问﹐我承认看错题。不过其实这些是鸡同蛋的问题﹐转过形式便PROVE到﹐不至于COMPLETELY WRONG 嘛 2009-02-01 19:26:10 补充： (a_11+a_21+...+a_n1)x_1+(a_12+a_22+...+a_n2)x_2+...+(a_1n+a_2n+...+a_nn)x_n =1 (GIVEN) x_1+x_2+...+x_n=1 (GIVEN) 2009-02-01 19:26:16 补充： SUBSTRACT (a_11+a_21+...+a_n1-1)x_1+(a_12+a_22+...+a_n2-1)x_2+...+(a_1n+a_2n+...+a_nn-1)x_n=0 As x_1
x_2
...x_n are positive =>a_11+a_21+...+a_n1-1=0
...a_1n+a_2n+...+a_nn-1=0 So A
a square matrix of order n
is a stochastic matrix.
You are pletely wrong! Why on earth do you show the converse of the proposition! 2009-02-01 15:59:05 补充： 1. Denote entry at i-th row and j-th colm of matrice A be A(i
j) Let M = A*x
then
M(i) = SUM[j] A(i
j)*x(j) Suppose M is stochastic
SUM[i] M(i) = 1
that is
SUM[i] SUM[j] A(i
j)*x(j) = 1
grouping x(j) terms and factorizing gives SUM[j] SUM[i] A(i
j) *x(j) = 1; on the other hand
as x itself is stochastic
SUM[j] x(j) = 1. As all x(j) are positive
the weights 1
1
1
1...
1 are unique! Thus
SUM[i] A(i
j) = 1
Therefore
A itself is also stochastic. . 2. Take A = [ 1 1 ; 2 2 ]
B = I
C = [ 2 2 ; 1 1 ] A*B and B*C are m trivially
but AC = [ 3 3 ; 6 6 ] =\= CA = [ 6 6 ; 3 3 ] Thus the statement is false. . Remarks: Note that stochastic matrix is also called trition matrix
and is the matrix representation of markov chain. In fact
for any stochastic M
M^n is also stochastic for all natural number n. 2009-02-01 16:00:44 补充： oops
we should point out that: all A(i
j)>=0 2009-02-01 16:07:19 补充： The proof of this point is quite abstract. M(i) = SUM[j] A(i
j)*x(j) >= 0 as M is stochastic As our matrix A is fixed and x is arbitrary stochastic column vector
taking x = [1
0
..
0] gives A(i
1) >= 0 for all i taking x = [0
1
0
...
0] gives A(i
2) >= 0 for all i ... Similarly
it holds for all i
j
2009-02-01 16:09:15 补充： This is actually the key of attempting proof -- "we have to check that ALL the conditions are satisfied"!

论文阅读Stochastic Variance Reduced Ensemble Adversarial Attack for Boostingthe Adversarial

该论文发表于CVPR2022

链接：https://openaccess.thecvf.com/content/CVPR2022/papers/Xiong_Stochastic_Variance_Reduced_Ensemble_Adversarial_Attack_for_Boosting_the_Adversarial_CVPR_2022_paper.pdf

代码：https://github.com/JHL-HUST/SVR

Abstract

在这项工作中，我们将迭代集成攻击视为随机梯度下降优化过程，其中不同模型上梯度的方差可能导致局部最优值不佳。为此，我们提出了一种新的攻击方法，称为随机方差降低集成（SVRE）攻击，它可以减少集成模型的梯度方差并充分利用集成攻击。标准ImageNet数据集的实证结果表明，所提出的方法可以提高对抗性可迁移性，并显着优于现有的集成攻击。

Related Works

Input transformation attacks输入转换攻击。这种攻击侧重于采用各种输入转换来进一步提高对抗示例的可移植性。Xie等[35]提出了多样化输入法(DIM)[35]，利用随机调整大小和填充来创建不同的输入模式来生成对抗示例。Dong等[4]提出了平移不变量方法(TIM)，该方法优化了一组平移图像上的扰动。Lin等[16]发现了深度学习模型的尺度不变性，并提出了尺度不变性方法(scale-invariant Method, SIM)，该方法优化了输入图像的尺度副本上的对抗性扰动。Wang等[32]提出了Admix，计算输入图像上的梯度，混合一小部分每个外附图像，以制作更可转移的对手。

Model ensemble attacks模型集成攻击。Liu等[17]发现同时攻击多个模型也可以提高攻击的可移植性。他们将多个模型的预测融合在一起，得到集合预测的损失，并采用现有的对抗攻击(例如FGSM和PGD)，使用损失生成对抗示例。Dong等[3]提出了模型集成攻击的两种变体，分别是融合对数和融合损失。相比于对梯度优化或输入变换的各种探索，对模型集成攻击的研究要少得多，现有方法只是简单地融合输出预测、logits或损失。

我们的方法受到为随机优化而设计的随机方差减少梯度(SVRG)方法[12]的启发，该方法有一个外部循环，在一批数据上保持平均梯度，而一个内部循环，从批数据中随机抽取一个实例，并根据方差减少计算梯度的无偏估计。

在我们的方法中，我们将集成模型视为外环的数据批，并在内环的每次迭代中随机绘制一个模型。外部循环以良性图像作为初始对抗样例，计算这批模型的平均梯度，并将当前样本复制到内环，内环进行多次迭代的内部对抗样例更新。在每次内部迭代中，SVRE计算随机选择模型上的当前梯度，由该随机选择模型和集成模型上的外部对抗示例的梯度偏差调整。在内部循环的末尾，使用最新的内部对抗示例的调优梯度更新外部对抗示例。

通过这种方式，SVRE可以在外部循环获得更准确的梯度更新，以避免糟糕的局部最优，从而使精心制作的对抗示例不会“过拟合”集成模型。因此，精心设计的对抗示例预计对其他未知模型具有更高的可移植性。据我们所知，这是第一个通过在多个模型上的梯度方差透镜来研究现有集成攻击的局限性的工作。

Methodology

已存在的集成攻击方法：

集成攻击是增强对抗可转移性的有效策略。它的基本思想是使用多个模型生成对抗实例。

综合预测。Liu等首次提出通过平均模型的预测(预测概率)来实现集合攻击。对于K个模型的集合，集合模型的损失函数为:

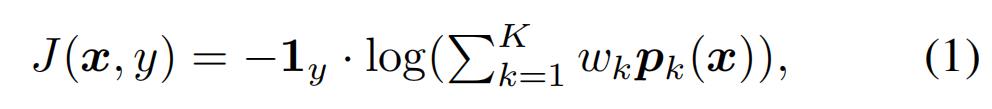
其中1y是x的ground-truth标签y的one-hot编码，PK是第K个模型的预测，wk≥0是受

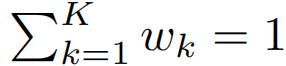
约束的集合权值。

logits上的集合。Dong等[3]提出融合模型的logits(输出在softmax之前)。对于K个模型的集合，在logits上集合的损失函数为:

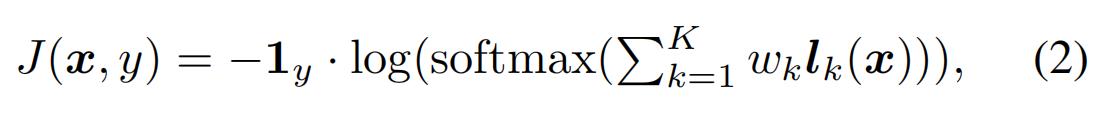
其中lk是第K个模型的logits。

损失合算。Dong等[3]还引入了一种可选的集成攻击，通过对K个模型的损失进行平均，如下所示:

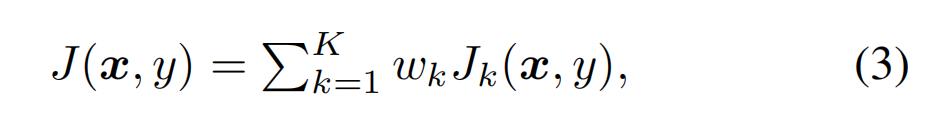
其中Jk是第K个模型的损失。

对于权重参数，三种方法都简单地选择了实验中的平均权重，即wk = 1/K。

从直观上看，现有的集成攻击方法有助于提高对抗可转移性，因为攻击集成模型可以帮助找到更好的局部极大值，并且更容易推广到其他黑盒模型。但是，仅仅对模型的输出(logits、预测或损失)进行平均来建立对抗攻击的集成模型可能会限制攻击性能，因为不同模型的单个优化路径可能会有差异，但没有考虑方差，导致对集成模型的过拟合。

Method

我们观察到现有的模型集成攻击方法只是直接融合所有模型的输出，而忽略了不同模型上梯度的变化，这可能会限制模型集成攻击的潜在能力。由于模型架构的固有差异，模型的优化路径可能存在较大差异，这表明可能的模型之间在梯度方向方差上存在较大差异。这种方差可能会导致集成攻击的优化方向不太准确。因此，转移的对抗实例的攻击能力相当有限。为了解决这一问题，我们提出了一种称为随机方差减少集成攻击(SVRE)的新方法来增强集成攻击的对抗可转移性。

我们的方法受随机方差减少梯度(SVRG)方法[12]的启发，该方法设计用于随机优化，它有一个外环，在一批数据上保持平均梯度，一个内环，从批中随机抽取一个实例，并根据方差减少计算梯度的无偏估计。

在我们的方法中，我们将集成模型作为外循环的批数据，在内循环的每次迭代中随机绘制一个模型。将良性图像作为初始对抗样例，外循环计算该批模型的平均梯度，将当前样例复制到内循环，内循环对内部对抗样例进行多次迭代更新。在每一次内部迭代中，SVRE计算一个随机选择的模型上的当前梯度，由该随机选择模型和集成模型上的外部对抗示例的梯度偏差调整。在内部循环的最后，外部对抗示例将使用最新的内部对抗示例的调整梯度进行更新。

Stochastic Variance Reduced Ensemble Attack

在本文中，将迭代集成攻击视为一个随机梯度下降优化过程，在每次迭代中攻击者选择一批集成模型进行更新，在对抗样本生成过程中，不同模型上的梯度方差可能会导致局部最优性较差，因此，我们的目标是减小梯度方差，以稳定梯度更新方向，使诱导的梯度更好地推广到其他可能的模型。

Ens：传统的模型集合攻击方法。

受为随机优化设计的随机方差减少梯度(SVRG)方法[12]的启发，我们提出了一种随机方差减少集成攻击方法来解决模型的梯度方差，从而充分利用集成攻击。SVRG的基本思想是利用预测方差缩减来减小随机梯度下降(SGD)的固有方差，而我们的目标是减少多个模型的固有梯度方差。本文提出的方法与传统模型的主要区别在于SVRE有一个内部更新循环，SVRE通过M次更新获得方差降低的随机梯度

具体：

首先通过对模型的一次遍历得到多个模型的梯度,并且在M次内部迭代中保持这个值。

然后，从模型集合中随机选取一个模型，在方差缩减后得到随机内部梯度，并利用的累计梯度更新内部对抗样本。

最后，使用一个内部循环的累积梯度更新外部梯度，由于是的无偏估计，有助于减少不同模型上的梯度。