备战蓝桥 2021-12-31

Posted 2022-01-29 一个数学不怎么好的程序员

目录

• 二分查找
• • 题目
  • 思路
• 移除元素
• • 题目
  • 思路
• 带分数
• • 题目

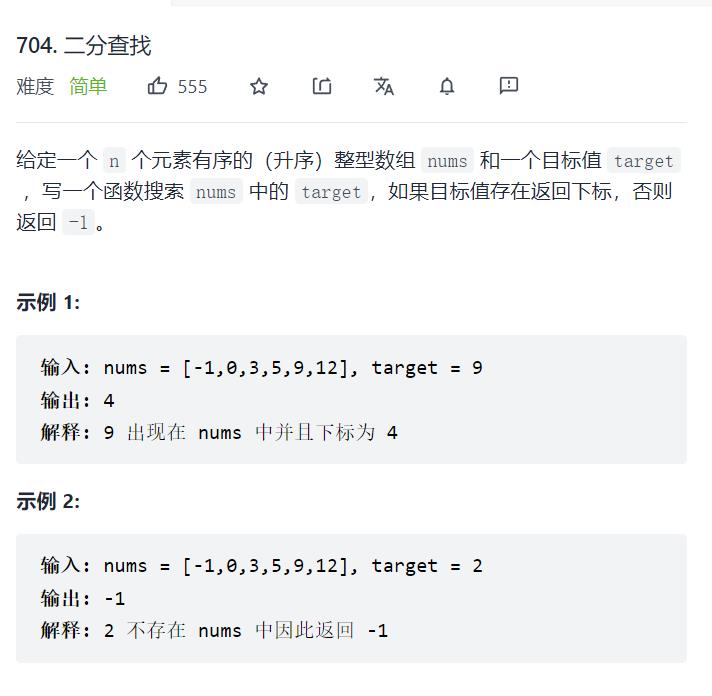
二分查找

题目

思路

这道题就是一道很简单的二分查找，但也有我们很多要注意的地方，区间的划分最为关键。
其实区间划分的问题，一般我们有两种区间划分的方法，1，[left,right-1] 2,[left,right) ,这两种划分是等价的，其次你还要搞明白，[right,right]这个区间是有意思的，因为你可以取到right这个位置的值，而[right,right)这个区间是没有意义的，因为你取不到right这个地方的值。当你明白了这几个点了之后，区间的划分就变的十分简单了。

首先的先用之前在y总那记的二分模板来写了下。

          /*  y总那学习的模板
          int r=nums.size()-1,l=0,mid=0;
          while(l<r)
          
              mid=(l+r)>>1;
              if(nums[mid]>=target)  r=mid;
              else l=mid+1;
          
          if(nums[r]==target) return r;
          else return -1;
          */

他的模板确实很简单，这是不易理解， 很多人可能第一感觉应该是写if(nums[mid]=target) return mid,其实是不行的，你只要去举几个例子就知道了，写成nums[r]和nums[l]都是可以的。

代码随想录那儿的两种写法
1，区间划分成[left，right]

//取左闭右闭区间
          /*int left=0,right=nums.size()-1; //因为是右闭，所以这儿right取nums.size()-1
          int mid=0;
          while(left<=right)  //这儿要有等于号，因为当left==right时，【right，right】这个区间也是有意义的
          
              mid=(left+right)>>1;
              if(nums[mid]>target)  right=mid-1;  // 此时说明答案在mid的左边，而且mid这个位置
                                                  //一定大于target，且区间是右闭，所以区间更新
                                                  // 为【0，mid-1】
              else if(nums[mid]<target) left=mid+1; //理由和推理同上
              else  return mid;
          
          return -1;*/

2,区间划分成[left,nums.size() )

 //左闭右开的写法
          int left=0,right=nums.size(); //因为右区间开的，所以区间[0,nums.size() )可以确保遍历
                                        //完整个数组 
          int mid=0;
          while(left<right)   //因为是左开右闭，所以当left==right时，[right,right)这个区间是没有
                              //意义的
        
            mid=(left+right)>>1;
            if(nums[mid]>target)  right=mid; //此时说明答案在左区间[left,mid-1],而这种情况的
                                             //为左开右闭，所以区间[left,mid)等价于[left,mid-1]
            else if(nums[mid]<target)  left=mid+1; // 此时说明答案在右区间[mid+1,nums.size-1]
                                                   // 而区间[mid+1,nums.size)等价于此区间
            else return mid;
        
        return -1;

移除元素

题目

思路

首先要明白一点，要想从数组中移除元素肯定是不可能的，因为数组中的空间是连续的，所以我们只能采用元素覆盖的方法，想到这，一个思路也就来了：我们可以用一个for循环遍历数组，找到等于val的位置，然后将其之后的元素往前移一位，达到覆盖它的目的。

    int size=nums.size();
    for(int i=0;i<size;i++)
    
        if(nums[i]==val)
        
            for(int j=i+1;j<size;j++)
            
                    nums[j-1]=nums[j];
            
            i--;
            size--;
        
    
    return size;

注意：要记得i–和size–，因为你将后面所有的元素往前移一位时，你i本身这个位置也要往前移一位，同时你覆盖了你个等于val的位置，所以要size–。

像这种两层for循环可以暴力求解的题目，往往可以用双指针来优化，已达到用一个for循环就可以做出来的目的。

        /*  双指针法
        int fast=0,slow=0;
        for(fast=0;fast<nums.size();fast++)
        
            if(nums[fast]!=val)
            
                nums[slow++]=nums[fast];
            
        
        return slow;

带分数

题目

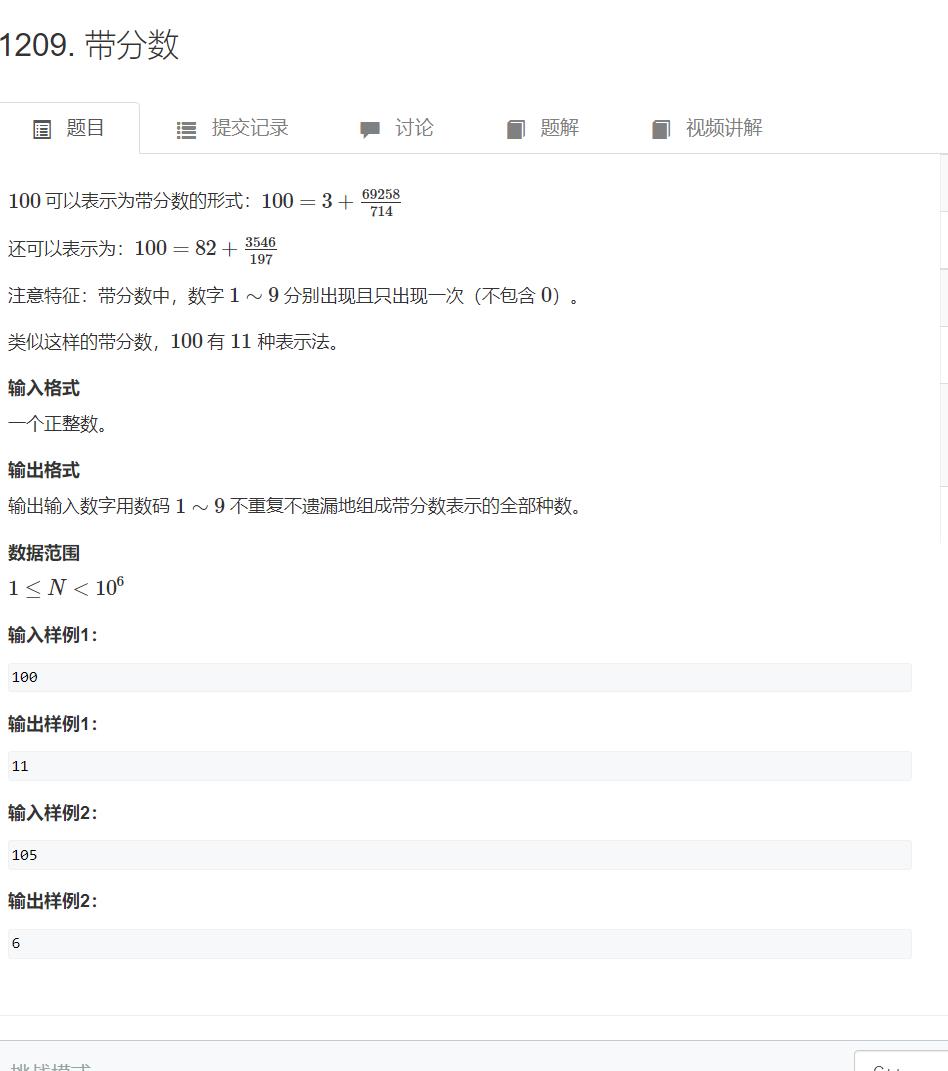
刚拿到这题时我是迷茫的，根本没有任何的思路，我一开始想找找看，是否具有什么规律，发现并不行，因为你无法确保它里面包含每一个数字。后来看了题解之后，才恍然大悟，既然我们不能正向推导，保证它里面包含所有的数字，那为什么我们不反过来想了，我们列举出1到9的所有全排列，然后将这9个数分成3组，分别对应这a，b，c，这样就确保了a，b，c这三个数中一定包含了1到9，而且不会有重复，之后我们判断a，b，c这三个数是否满足等于n的关系即可。

#include<iostream>
using namespace std;
const int N=10;
int backup[N]; //用来存放不同排列组合结果的数组
bool st[N];
int n;
int res;

int cal(int l,int r)  //将数组中的数分离出来的方法。

    int ans=0;
    for(int i=l;i<=r;i++)
    
        ans=ans*10+backup[i];
    
    return ans;



void dfs(int u)

    if(u>9)  //因为数组是从1开始放的，所以最后结束的时候是10
    
        for(int i=1;i<8;i++)   //因为存放的数组是从1开始的
        
            for(int j=i+1;j<9;j++)
            
                    int a=cal(0,i);
                    int b=cal(i+1,j);
                    int c=cal(j+1,9);
                    if(a*c+b==n*c)
                    
                        res++;
                    
            
        
        return ;
    
    
    for(int i=1;i<=9;i++)
    
        if(!st[i])
        
            st[i]=true;
            backup[u]=i;
            dfs(u+1);
            backup[u]=0;
            st[i]=false;
        
    


int main()

    cin>>n;
    dfs(1);  //按照我正常的习惯，做dfs时数组从第一个位置开始放      
    cout<<res<<endl;
    return 0;