用于游戏开发和其他目的的光线投射教程
Posted 妇男主任
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了用于游戏开发和其他目的的光线投射教程相关的知识,希望对你有一定的参考价值。
用于游戏开发和其他目的的光线投射教程
前言
本文档探讨了光线投射背后的基本理论,这是一种在 90 年代游戏开发领域非常流行的伪 3 维渲染技术。通常,本文档不会涉及实现和编码细节。讨论将主要关于概念,实现取决于读者。对于普通读者,假设了解勾股定理和高中数学知识。
本文档写于 1996 年,尽管光线投射已被更新、更强大的技术(和硬件!)所取代,但读者仍有望从该技术中受益。
介绍
过去几年,个人电脑市场出现爆炸式增长*。这种增长部分是由对多媒体标题的兴奋和好奇产生的。本项目是尝试在多媒体标题开发过程中获得一些知识和经验。具体来说,我们将仔细研究与3D多媒体游戏开发相关的问题。
(*本文档写于 1996 年)
一个简短的历史
1992 年,随着一款游戏《德军总部 3D》(iD Software)的发布,光线投射的轰动开始了。在 Wolfenstein 3D 中,玩家被放置在一个 3D 迷宫般的环境中,他/她必须在与多个对手作战时找到出口。Wolfenstein 3D 因其快速流畅的动画而成为即时经典。使这种动画成为可能的是一种称为“光线投射”的创新 3 维渲染方法。
Wolfenstein 3D 由 Id Software 开发和创建。从今以后,Id 的程序员 John Carmack 很可能是发起光线投射感觉的人(Myers 5)。
什么是光线投射
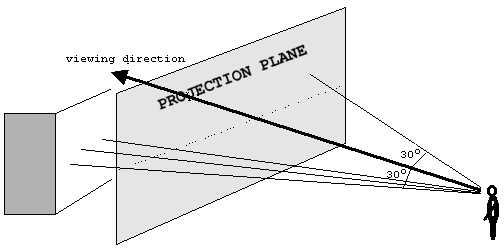
光线投射是一种技术,它通过将光线从视点追踪到观看体 (LaMothe 942)来将有限形式的数据(非常简化的地图或平面图)转换为 3D 投影。例如,光线投射变换在下图中。

请注意,这不是光线投射的唯一应用。光线投射也可用于渲染地形图,例如图 2(下图)。要记住的重点是光线投射“从观察者的眼睛向后追踪光线到物体”。
用于游戏开发的光线投射与光线追踪
与光线投射一样,光线追踪“通过追踪从观察者的眼睛到场景中物体的假想光线来确定表面的可见性”(Foley 701)。
从这两个定义来看,光线投射和光线追踪似乎是一样的。事实上,有些书籍交替使用这两个术语。然而,从游戏程序员的角度来看,光线投射被视为光线追踪的一种特殊实现(子类)。
之所以做出这种区分,是因为一般而言,光线投射比光线追踪快。这是可能的,因为光线投射利用一些几何约束来加速渲染过程。例如:墙壁总是与地板垂直(您可以在 Doom 或 Wolfenstein 3D 等游戏中看到这一点)。如果没有这样的限制,光线投射将是不可行的。例如,我们不想对任意样条进行光线投射,因为很难找到对此类形状的几何约束。
表 1是光线投射和光线追踪之间的一般比较。要记住的要点是,由于某些“几何约束”,在光线投射中要跟踪的“光线数量较少”。或者,也可以说光线投射是光线追踪的一种特殊用途的实现。
表 1:光线投射和光线追踪之间的比较
(游戏程序员/游戏开发者的观点)

光线投射的局限性
光线投射很快,因为它利用了一些几何约束。在大多数情况下,墙壁始终与地板成 90 度角。(请注意,我们不是在谈论墙壁和另一面墙壁之间的角度,而是墙壁和地板之间的角度。)
因此,光线投射游戏几乎存在的一个限制是视点不能沿 Z 轴旋转(图 5)。如果允许这样做,则墙壁可能会倾斜,从而失去绘制垂直切片的好处。这种无法沿 Z 轴旋转是光线投射环境不被视为真正的 3D 环境的原因之一。

在光线投射环境中,玩家可以向前、向后、向左或向右转;但不能绕Z轴旋转/摆动(这种Z轴旋转称为倾斜)。
光线投射第 1 步:创造一个世界
为了说明光线投射的过程,我们将创建一个具有以下几何约束的迷宫世界:
- 墙壁始终与地板成 90° 角。
- 墙壁由大小相同的立方体组成。
- 地板总是平坦的。
出于我们的目的,每个立方体的大小为 64x64x64 单位。(选择 64 是任意的,但选择 2 的倍数会很有用;因为我们可以对这样的数字执行一些算术移位运算(移位运算比乘法或除法快)。大小越大立方体,世界看起来会更块,但较小的立方体会使渲染速度变慢。)
这样的世界如 下图 所示。
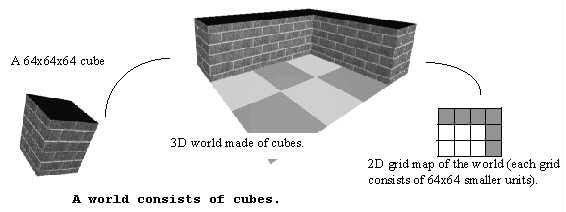
在继续之前,我们将定义我们的坐标系,以免混淆。我们使用的坐标系如下:
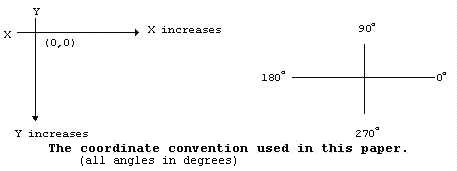
注意:任何类型的笛卡尔坐标系都可以正常工作。但是,您必须保持一致(不要对一件事使用自上而下的坐标系,而对其他事使用自上而下的坐标)。如果你这样做,你可能会让自己感到困惑——我做到了。
光线投射第 2 步:定义投影属性
现在我们有了世界,我们需要定义一些属性,然后才能投影和渲染世界。具体来说,我们需要知道这些属性:
- 玩家/观众的高度、玩家的视野(FOV)和玩家的位置。
- 投影平面的尺寸。
- 播放器与投影平面的关系。
玩家应该能够看到他/她面前的东西。为此,我们需要定义一个视野 (FOV)。FOV 决定玩家看到他/她面前的世界的宽度(见下图)。大多数人的 FOV 为 90 度或更多。然而,这个角度的 FOV 在屏幕上看起来并不好。因此,我们通过试验和实验(关于它在屏幕上看起来有多好)将 FOV 定义为 60 度。玩家的高度被定义为 32 个单位,因为考虑到墙壁(立方体)高 64 个单位,这是一个合理的假设。
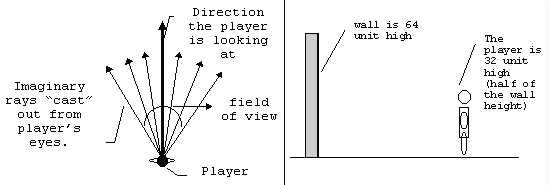
要将玩家置于世界中,我们需要定义玩家的 X 坐标、玩家的 Y 坐标以及玩家面对的角度。这三个属性构成了玩家的“观点”。
假设玩家以相对于世界的 45 度视角放置在网格坐标(1,2)中间的某个位置,那么玩家的视角和 FOV 将如下图 所示。(一个网格组成是 64 x 64 个单位。因此,我们也可以说玩家在单位坐标(96,160)中)。
播放器位于网格坐标(1,2)或单位坐标(96,160)中间,视角为 45 度,视野为 60 度。
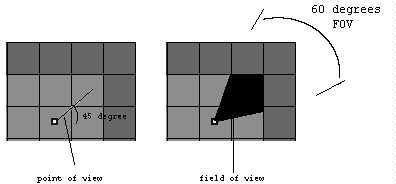
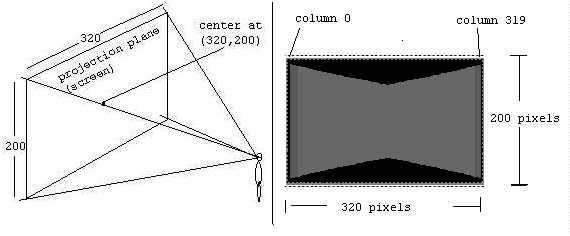
我们需要定义一个投影平面,以便我们可以将玩家看到的东西投影到投影平面中。320 单位宽和 200 单位高的投影平面是一个不错的选择,因为这是大多数 VGA 视频卡的分辨率。(视频分辨率通常以像素为单位,因此可以将 1 像素视为等于 1 个单位。)
当玩家的视角被投影到投影平面时,世界应该看起来像下面中的场景。

寻找到投影平面的距离
通过知道视野(FOV)和投影平面的尺寸,我们可以计算出后续光线之间的角度以及玩家与投影平面之间的距离。
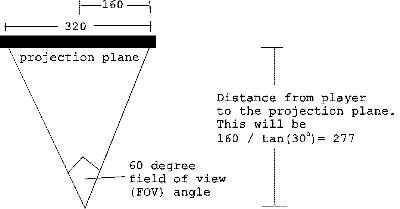
这是我们可以计算的(其中大部分是高中数学,如果你不明白,我建议你复习三角学/勾股定理):
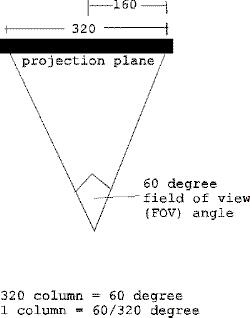
所以现在我们知道:
- 投影平面的尺寸 = 320 x 200 个单位
- 投影平面的中心 = (160,100)
- 到投影平面的距离 = 277 个单位
- 后续光线之间的角度 = 60/320 度
(我们偶尔会将“后续光线之间的角度”称为“后续列之间的角度”。稍后,这个角度将用于从一列到另一列循环。玩家到投影平面之间的距离将用于缩放。)
光线投射第 3 步:寻找墙壁
可以将墙视为 320 条垂直线(或 320 条墙切片)的集合。
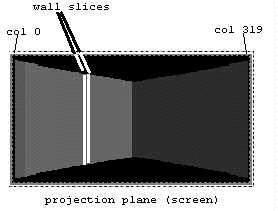
这正是一种适用于光线投射的几何约束形式。我们可以只跟踪屏幕的每个垂直列,而不是为屏幕上的每个像素跟踪一条光线。FOV 最左侧的光线将投影到投影平面的第 0 列,最右侧的光线将投影到投影平面的第 319 列。
寻找墙壁的光线
因此,为了渲染这样的场景,我们可以简单地从左到右追踪 320 条光线。这可以在循环中完成。以下说明了这些步骤:
- 根据视角,减去 30 度(FOV 的一半)。
- 从第 0 列开始:
A. 投一缕。(术语“施法”有点令人困惑。想象一下玩家是一个可以“施放”射线而不是法术的巫师。射线只是从玩家延伸出来的“假想”线。)
B. 跟踪光线,直到它碰到墙壁。 - 记录到墙壁的距离(距离等于射线的长度)。
- 添加角度增量,使光线向右移动(我们从图 10 中知道,角度增量的值为 60/320 度)。
- 对每个后续列重复步骤 2 和 3,直到投射所有 320 条光线。
步骤 2A的技巧是,我们只需检查每个网格,而不是检查每个像素。这是因为墙只能出现在网格边界上。考虑如下面所示跟踪的光线。要检查这条射线是否撞到了墙壁,只需检查 A、B、C、D、E 和 F 处的网格交点即可。
这条射线在 A、B、C、D、E 和 F 点与网格相交
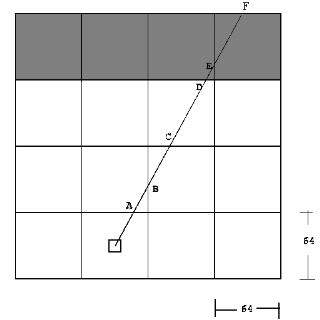
要找到墙壁,我们需要检查射线遇到的任何网格交点;并查看网格上是否有墙。最好的方法是分别检查水平和垂直交叉点。当垂直或水平交叉口上有墙时,检查停止。然后比较到两个交点的距离,并选择更近的距离。以下两幅图说明了此过程。
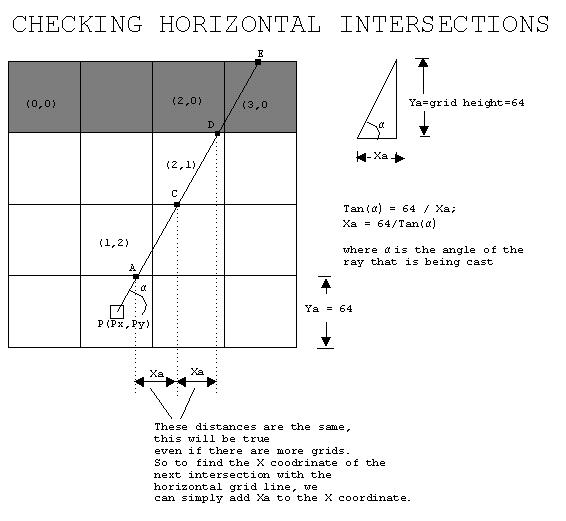
找水平网格线交点的步骤:
- 找到第一个交点的坐标(本例中的点 A)。
- 找Ya。(注意:Ya只是网格的高度;但是,如果光线朝上,Ya将为负,如果光线朝下,Ya将为正。)
- 使用上面给出的等式找到 Xa。
- 检查交点处的网格。如果网格上有墙,停下来计算距离。
- 如果没有墙,则将 延伸到下一个交点。请注意,下一个交点的坐标 - 称之为 (Xnew,Ynew) 是 Xnew=Xold+Xa,并且 Ynew=YOld+Ya。
例如,以下是您如何获得 A 点:
注意:记住笛卡尔坐标向下增加,任何小数值都将向下舍入。
====== 寻找水平交点 ======
1.求A的坐标,
如果光线朝上
Ay = rounded_down(Py/64) * (64) - 1;
如果光线朝下
Ay = rounded_down(Py/64) * (64) + 64;
(图中光线朝上,所以我们使用
第一个公式
。Ay=rounded_down(224/64) * (64) - 1 = 191;
现在,我们可以找到y的网格坐标。
但是,我们必须确定 A 是否是该线上方块的一部分,
或该线下方的块。
在这里,我们选择将A作为线上方块的一部分,这就是我们从Ay中减去1的原因,
所以Ay的网格坐标为 191/64 = 2;
Ax = Px + (Py-Ay)/tan(ALPHA);
图中,(假设ALPHA为60度),
Ax=96 + (224-191)/tan(60) = 约115;
Ax 的网格坐标为 115/64 = 1;
所以 A 在网格 (1,2) 处,我们可以检查该网格上是否有墙。
(1,2) 上没有墙,所以光线会延伸到 C。
2. 寻找 Ya
如果光线朝上
Ya=-64;
如果光线朝下
Ya=64;
3. 寻找 Xa
Xa = 64/tan(60) = 36;
4、我们可以得到C的坐标如下:
Cx=A.x+Xa=115+36=151;
Cy=A.y+Ya = 191-64 = 127;
将每个分量除以64 将其转化为网格坐标,结果为
Cx = 151/64 = 2(网格坐标),Cy = 127/64 = 1(网格坐标)
所以C的网格坐标为(2, 1) . (C 程序员注:记住我们总是向下取整,
尤其如此,因为
您可以使用右移 8 来除以 64)。
5. 网格 (2,1) 被选中。再次,没有墙,所以射线延伸到 D。
6. 我们可以得到 D 的坐标如下:
Dx=C.x+Xa = 151+36 = 187;
Dy=C.y+Ya = 127-64 = 63;
将
每个分量除以64 将其转化为网格坐标,
结果为
Dx = 187/64 = 2(网格坐标),
Dy = 63/64 = 0(网格坐标)
所以D的网格坐标为(2, 0) .
6. 网格 (2,0) 被选中。
那里有一堵墙,所以过程停止。
(可以看到,一旦我们有了Xa和Ya的值,这个过程就很简单了,我们只要把旧的值与Xa和Ya不断相加,并进行移位操作,就可以找出下一个的网格坐标被射线击中的点。)
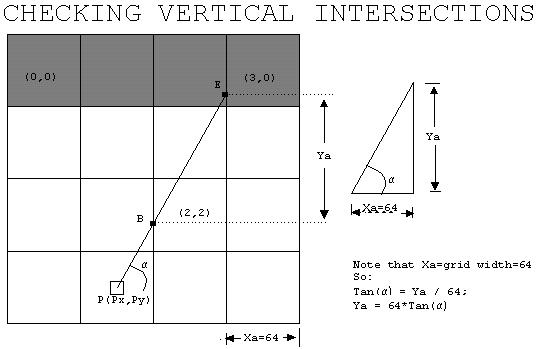
寻找垂直网格线交点的步骤:
- 找到第一个交点的坐标(本例中的点 B)。光线在图片中朝右,所以 Bx = rounded_down(Px/64) * (64) + 64。
如果光线朝左 Bx = rounded_down(Px/64) * (64) – 1. Ay = Py + (Px-Ax)*tan(ALPHA); - 找到 Xa。(注意:Xa 只是网格的宽度;但是,如果光线朝右,则 Xa 将为正,如果光线朝左,则 Ya 将为 负。)
- 使用上面给出的等式找到 Ya。
- 检查交点处的网格。如果网格上有墙,停下来计算距离。
- 如果没有墙,则将 延伸到下一个交点。请注意,下一个交点的坐标 - 称之为 (Xnew,Ynew) 只是 Xnew=Xold+Xa,而 Ynew=YOld+Ya。
在图中,首先,光线击中点 B。网格 (2,2) 被选中。(2,2) 上没有墙,所以射线延伸到 E。网格 (3,0) 被检查。那里有一堵墙,所以我们停下来计算距离。
在此示例中,点 D 比 E 更近。因此将绘制 D(不是 E)处的墙切片。
寻找到墙壁的距离
有几种方法可以找到从视点(玩家)到墙壁切片的距离。它们如下图所示。
查找到墙壁切片的距离

正弦或余弦函数的实现成本更低,因为它们可以预先计算并放入表格中。这是可以做到的,因为 ALPHA(玩家的 POV)必须在 0 到 360 度之间,所以可能性的数量是有限的(平方根方法对 x 和 y 的可能值几乎没有限制)。
在画墙之前,有一个问题是必须要解决的。这个问题被称为“鱼缸效应”。鱼缸效应的发生是因为光线投射实现将极坐标和笛卡尔坐标混合在一起。因此,在不直接位于观察者面前的墙壁切片上使用上述公式将提供更长的距离。这不是我们想要的,因为它会导致如下图所示的观看失真。

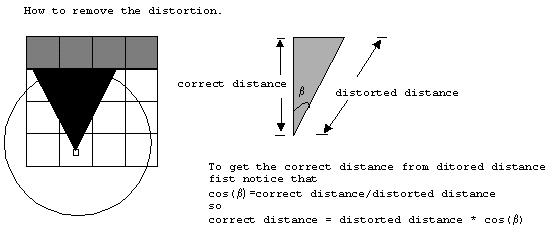
因此,为了消除观看失真,从上图 中的方程获得的最终距离必须乘以 cos(BETA);其中 BETA 是投射的光线相对于视角的角度。在上图中,视角 (ALPHA) 为 90 度,因为玩家面朝上。因为我们有 60 度的视野,所以最左边的光线的 BETA 是 30 度,最右边的光线是 -30 度。
画墙
在前面的步骤中,投射了 320 条光线,当每条光线击中墙壁时,计算到该墙壁的距离。知道距离,然后可以将墙切片投影到投影平面上。为此,需要找到投影墙切片的高度。事实证明,这可以通过一个简单的公式来完成:
实际切片高度
投影切片高度 = --------------------- * 到投影平面的距离
到切片的距离
下面的图 解释了该公式背后的逻辑
墙壁缩放背后的数学

我们的世界由立方体组成,其中每个立方体的尺寸为 64x64x64 单位, 所以墙高是64个单位。我们也已经知道玩家到投影平面的距离(277)。因此,方程可以简化为:
投影切片高度 = 64 / 到切片的距离 * 277
在实际实现中,可以考虑以下几点:
-
例如,可以预先计算 64/277,因为这将是一个常数值。一旦计算出来,就可以在屏幕上绘制墙切片。这可以通过简单地在投影平面(屏幕)上的相应列上绘制一条垂直线来完成。
-
还记得数字 277 是从哪里来的吗?这个数字实际上可以稍微偏离一点,而不会造成太大的影响。事实上,使用255的值会节省时间,因为程序员可以使用移位运算符来节省计算时间(右移3进行乘法,左移进行除法)。
例如,假设第 200 列的光线在 330 个单位的距离处撞击墙壁切片。切片的投影将为 64 / 330 * 277 = 54(向上取整)。
由于投影平面的中心被定义为 100。墙切片的中间应该出现在这一点上。因此,应绘制墙切片的顶部位置是 100-27=73。(其中 27 是 54 的二分之一)。最后,切片的投影将类似于下图。

纹理贴图墙
为了使墙壁更具吸引力,可以使用称为纹理映射的技术在墙壁上绘制纹理(位图)。(纹理映射通常是指在表面上绘制位图/纹理的技术。)对于立方体世界,我们使用大小为 64 x 64 像素的位图。选择这个大小是因为 64 x 64 也是我们在我们的世界中使用的立方体面的大小。可以使用不同大小的位图,但使用相同大小会简化纹理映射过程。
如果我们要将纹理映射到任意多边形上,纹理映射过程会很复杂。幸运的是,在我们正在创建的光线投射世界中,纹理映射只是缩放位图切片(一列)的问题(参见下面的图)。

当光线寻找墙壁交点时,可以很容易地找到偏移量(光线相对于网格的位置)。然后可以使用该偏移量来确定位图的哪一列将被绘制为墙切片。下图说明了查找偏移量的过程。
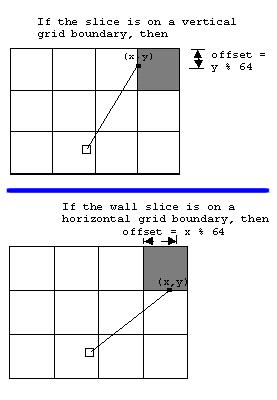
绘制地板
要绘制地板,我们可以进行地板浇铸(floor-casting 是指渲染地板的一种技术)。但是请注意,在没有纹理映射或着色的情况下执行地板铸造将是浪费的。换句话说,如果地板没有纹理或阴影(阴影将在后面探讨),那么我们可以简单地用纯色绘制地板,我们就完成了。牢记这一点,让我们探索进行地板铸造所需的条件。
有几种方法可以进行地板浇铸。但是,它们都使用类似的技术。该技术解释如下。
- 找到与地板的交点。
- 确定已经相交的地板的世界坐标。
- 计算玩家与地板交点的距离。
- 将地板交点投影到投影平面上。
请注意,没有必要绘制所有楼层。我们应该只绘制未被墙壁覆盖的地板。出于这个原因,我们应该从壁切片的底部开始铸造。从切片的底部,我们然后向下扫描投影平面上的每个像素(即:随后向下投射光线)。然而,这一次,光线不是寻找与墙壁的交点,而是寻找与地板的交点。

请记住,我们不需要投射超出投影平面。(即:从墙片底部开始,逐行向下投射;到达投影平面底部时停止。)
下面的图解释了地板浇铸背后的数学原理。
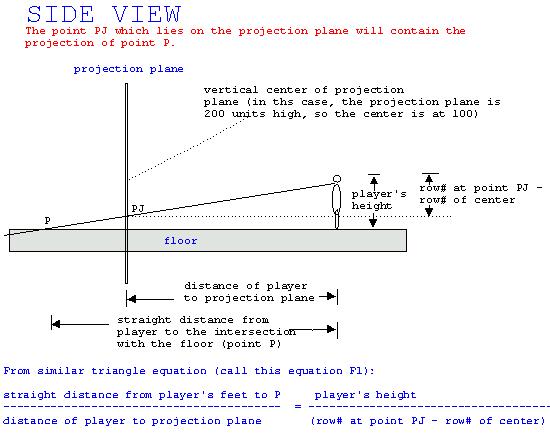
重申一下,请在阅读以下步骤时查看插图:
- 从墙切片的底部开始。
- 获取像素位置(您在进行墙壁投射时具有此值)。
- 从像素到观察者的眼睛画一条线(一条光线)。
- 延长线使其与地板相交。
- 线与地板“相交”的点是纹理贴图上被光线击中的点。
- 获取纹理贴图上那个点的像素值(参见下图,了解如何做到这一点)并将其绘制在屏幕上。
- 重复 1-5 直到到达屏幕底部。
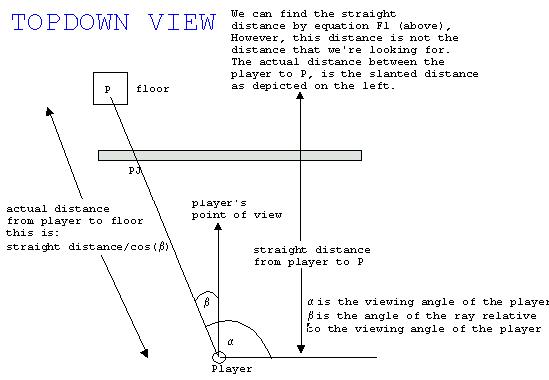
绘制天花板
要绘制天花板,可以颠倒地板浇筑过程。而不是从跟踪光线的底部在一个壁切片的向下方向,从追踪射线顶壁在向上方向。一旦掌握了地板铸造背后的理论,这实际上非常简单。
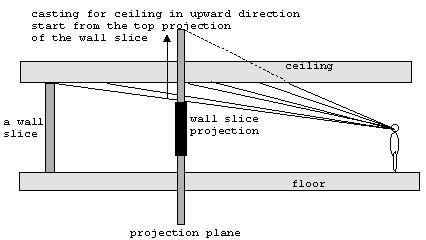
稍后,我们将解释如何模拟仰视、俯视、飞行和蹲伏的错觉。如果程序员不想模拟这些,可以同时绘制地板和天花板。这是因为玩家的眼睛到地板和天花板的距离相等/对称。(地板和天花板是对称的,因为玩家的眼睛正好在地板和天花板的中点。)
可变高度的墙
到目前为止,我们世界上所有的墙都具有相同的高度。通过一些创新,我们实际上可以使用不同高度的墙壁。这使世界变得更有趣,如下图所示。
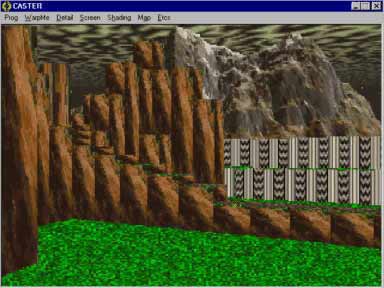
将可变高度墙概念化的最简单方法是将墙视为地板。也就是说,将墙壁想象成升高的地板。我们需要一个数组来保存每个地板网格的高度来完成这项工作。渲染场景的基本方法是这样的:
- 从投影平面的最左侧列开始。
- 找出玩家当前站立的地板的高度。(称之为 CURRENT_HEIGHT。)
- 像以前一样投射光线并检查交叉点。
- 如果光线击中高度与 CURRENT_HEIGHT 不同的地板,则该地板要么升高/下沉。(活动地板只是一堵墙。)
- 如果它被提升,那么它将是可见的。投影它,并渲染它。(下面的图 30 说明了这背后的数学原理。)
- 如果它沉没了,那么我们不需要对其进行投影,因为它将不可见。
- 从发生高度变化的点开始绘制地板,直到最后一个墙切片的顶部投影到的点。 (最初,最后一个墙切片的顶部将是投影平面的底部。)
- 重复直到射线延伸通过世界地图的限制。
- 对所有后续列重复步骤 2 到 8。
为了阐明这个过程,请考虑渲染下面图中的场景的过程。

首先跟踪击中 A 点(投影平面的最底行)的光线。当光线沿投影平面向上移动时,B点的壁被击中,因此绘制了切片BC。知道A点到B点没有高度变化,就绘制了A点到B点的地板。然后射线被延伸。它检测到 D 点的高度变化。因此,绘制了切片 DE。知道C点到D点没有高度变化,绘制C点到D点的地板。然后射线再次延伸。在 F 点,到达地图的边缘。由于不能再有高度变化,所以绘制了从 F 点到 E 点的地板,并重复该过程,直到渲染整个屏幕。
使用可变高度墙的主要缺点是渲染过程会相当慢。这是因为当最近的墙壁被击中时,光线不再停止。加快此过程的一种方法是设置可见距离,然后忽略超出该距离的任何内容。
可变高度墙背后的数学计算。

水平运动 // 让玩家移动
玩家至少应该能够以三种方式移动:向前、向后和转身。玩家的位置由坐标和视角定义。为了允许运动,还需要两个属性。它们是玩家的移动速度,以及玩家的转弯速度。玩家的移动速度定义了玩家向前或向后移动时应该移动多少个单位。玩家的转弯速度(以角度衡量)定义了玩家转弯时要增加或减少的角度。我们将讨论我们如何使用这些属性来允许运动。
A. 向前和向后移动。
我们将玩家的移动速度定义为 10 个单位。(通常,这可以是任何数字,但数字越大,运动就越不平滑。) 查找 x 和 y 位移的过程如下图所示。如果玩家向前移动,我们将 XDisplacement 添加到当前玩家的 X 坐标;并将 Ydisplacement 添加到当前玩家的 Y 坐标。如果玩家向后移动,我们将 XDisplacement 减去当前玩家的 X 坐标;并将 Ydisplacement 减去当前玩家的 Y 坐标。(始终检查世界/墙壁边界,以免玩家走出地图或穿过墙壁。)
根据玩家的速度查找位移(在本例中,玩家的速度以 10 个单位表示)。

B、转向。
车削过程实施起来非常简单。我们需要做的就是在当前玩家的视角上增加或减少一个角度增量 (aI)(每当转弯变成一个完整的圆圈时就环绕)。同样,较大的角度增量会导致运动看起来不太平滑。
上下看
可以模拟在光线投射环境中向上和向下看以及飞行和蹲伏的错觉。然而,请注意——这很重要——这里将要解释的技巧并不总是遵循正确的三维投影理论。即:这些是技巧,它们不是进行“真实”模拟的正确方法。
A. 上下看。
回想一下,投影平面是 200 个单位高。并且到此为止,我们始终将投影平面的垂直中心设置为正好在中间(即点 y=100)。因此,任何墙切片的中点都将在投影点 y=100 处绘制。事实证明,只需更改此值即可模拟向上或向下查找的效果。
也就是说,为了模拟仰视,我们不是将垂直切片的中心放在 y=100 处,而是将其放在 y>100 的点上(这类似于向上移动投影平面)。
类似地,为了模拟向下看,我们不是将垂直切片的中心放在 y=100 处,而是将其放在 y<100 处(这类似于向下移动投影平面)。
为什么这个技巧有效?希望下面的插图可以解释它。
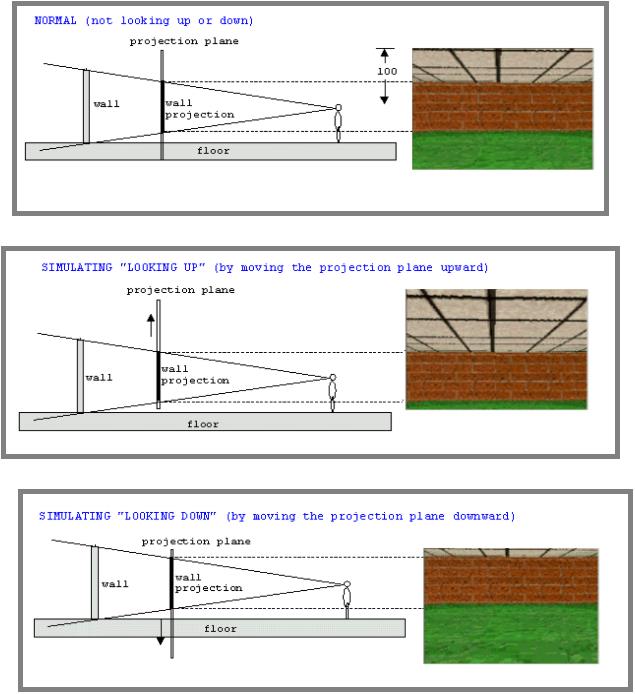
如果你感到困惑,想象一下站在你身后拿着一面墙的镜子,同时站直。当镜子向上或向下移动时,会显示墙壁的不同部分。镜子是投影平面。(在继续之前花点时间想象一下。)
飞行和蹲伏
回想一下,玩家的高度设置为 32 个单位。这意味着玩家的眼睛(假设玩家的眼睛正好在玩家的头顶上)正直视点 32 处的墙壁。由于 32 是墙壁高度的一半,因此玩家的高度为 32 会使玩家的眼睛位于地板和天花板之间的中间(见下图)。
如果我们改变这个值怎么办?令人惊讶的是(或可能不会),墙壁会根据玩家的身高是增加还是减少而向上或向下移动。
因此,为了让玩家仿佛在飞行(或跳跃),我们可以简单地增加玩家的高度。同样,为了让玩家好像她/他在蹲伏,我们可以降低玩家的高度。高度不应小于 0 或大于墙壁的高度,因为这样做会使玩家越过天花板或沉入地板。
下图显示了此方法为何有效。

如果您感到困惑,我们再次使用镜像方法来阐明其工作原理。想象一下,你站直了,在一个小房间里拿着一面镜子。背对墙壁站立。将镜子放在眼睛前面(即:您不必转头就能看到镜子)。现在,想象一下如果你蹲下看看镜子里的东西会发生什么。在镜子里,你应该看到墙壁的不同部分和更多的地板面积…就像本页的第二张图片… 希望你明白了。
镜子是投影平面,眼睛位置是玩家的高度。
这种垂直运动方法有一个反直觉的方面,那就是:
投影平面必须始终与玩家的眼睛垂直。(也就是说:投影平面必须始终与墙壁平行——它们不能以任何方式倾斜。)对此进行概念化的最佳方法是想象一个人通过相机镜头“瞄准”。人总是以 90 度角向前瞄准;即使他/她蹲伏或站在桌子上。
这样做的原因是使用这种方法时,我们不能像下图那样倾斜投影平面;因为如果我们旋转投影平面以遵循“正常”的眼睛方向,那么墙壁将倾斜(不再与投影平面平行);然后渲染过程必须考虑到这一点。这意味着将需要更复杂的计算,并且渲染过程将变得非常缓慢。

更真实的俯视应该是这样的:
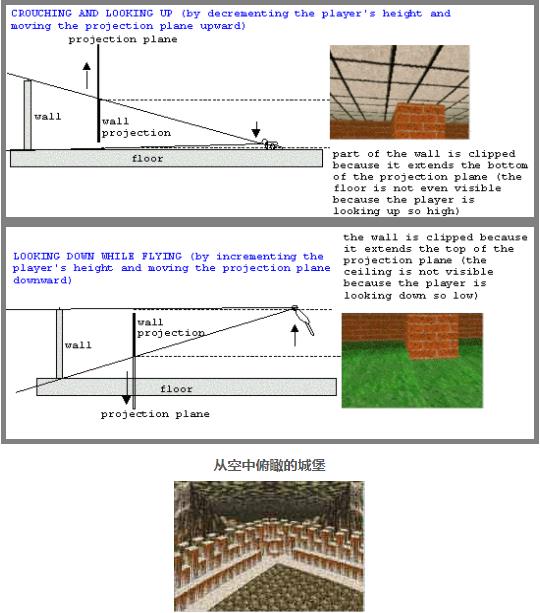
当你往下看时,你不仅会移动眼睛,还会移动头部,因此视角不同(与前6张图片相比)。本页描述的技术使用之前的技巧来“模拟”这一点。
综合效果
上面解释的效果可以结合起来创建更有趣的动作,如下图所示。
阴影
阴影
当一个物体离观察者更远时,该物体应该显得更暗/更亮。为了实现这一点,需要阴影效果。但首先,我们需要了解颜色是如何表示的。
标准的 256 色 VGA 模式寄存器包含调色板中每种颜色的 0 到 63 之间的三个数字,称为 RGB (RedGreenBlue) 值。例如,全红色具有 (63,0,0) 的 RGB 分量;全绿色有 (0,63,0); 全蓝有 (0,0,63)。诸如全黄之类的颜色,可以通过混合全红和全绿使(63,63,0)为黄色来获得。
要更改颜色的红色、绿色或蓝色分量的亮度,必须增加或减少表示颜色分量的数字。例如,要将具有 RGB 分量 (50,10,10) 的颜色的强度降低一半,请将每个分量乘以 0.5。生成的颜色将为 (25,5,5)。
这很简单,但是我们如何知道在什么距离上使用什么强度?第一个选项是使用一个精确的光强度公式,它是这样的:
强度 = (kI/(d+do))(NL)
从游戏程序员的角度来看,这个公式太复杂了,而且速度会非常慢,所以我们甚至不会去理会它。我们的主要目标将是制作看起来正确(或至少合理)的阴影效果。我们并不特别关心我们使用的公式是否是正确的教科书公式。
(旁注:对于游戏编程,我倾向于同意这个原则:
最好是拥有快速且看起来合理正确的东西;拥有完全正确但缓慢的东西。)
因此,改为使用以下公式(Lampton 406)。
强度 = 物体强度/距离 * 乘数
这里,Object Intensity是程序员希望使用的强度(它应该在 0 和 1 之间)。这实际上在概念上非常简单。它基本上是说随着物体变远,物体的强度变小。乘数是一个数字,以防止强度随距离下降到快速。这种实时计算仍然很昂贵,因此可以使用如下表所示的距离表:
| 到物体的距离 | 强度 |
| 0 到 500 | 1 |
| 501 至 1000 | 0.75 |
| 1001 至 1500 | 0.50 |
光线投射过程在这里非常有用,因为当我们投射光线时,我们还获得了到要渲染的对象的距离。在实际实现中,我们还需要考虑可用颜色的数量。由于大多数游戏只能使用 256 种颜色,因此需要进行一些操作以确保调色板包含正确的颜色范围。一个可能的解决方案是使用颜色匹配算法并将结果映射到强度表中。渲染时,我们只需从相应的表中获取正确的颜色值。(这非常快,因为一个特定的墙切片对于它的所有像素都具有相同的强度。所以我们只需要在墙切片之间切换表格。)
| 到物体的距离 | 强度 | 调色板映射表索引 |
| 0 到 500 | 1 | 1 |
| 501 至 1000 | 0.75 | 2 |
| 1001 至 1500 | 0.50 | 3 |
| … | … | … |
通常,当物体的强度接近零时,物体会显得更暗。然而,情况并非总是如此。我们可以通过改变“目标颜色”来创建有趣的效果,例如雾或水下效果。例如,要创建雾效果,我们可以使调色板收敛为白色。

其他参考内容、参考文献和注释
https://dev.opera.com/articles/3d-games-with-canvas-and-raycasting-part-1/
以上是关于用于游戏开发和其他目的的光线投射教程的主要内容,如果未能解决你的问题,请参考以下文章