BP神经网络中初始权值和阈值的设定

Posted 2023-05-05

代码如下：
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);
分别是什么意思，为什么要这么确定？

1、首先需要了解BP神经网络是一种多层前馈网络。

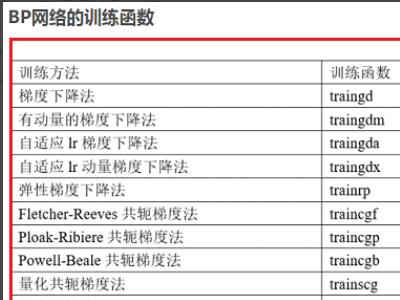
2、以看一下在matlab中BP神经网络的训练函数，有梯度下降法traingd,弹性梯度下降法trainrp，自适应lr梯度下降法traingda等。

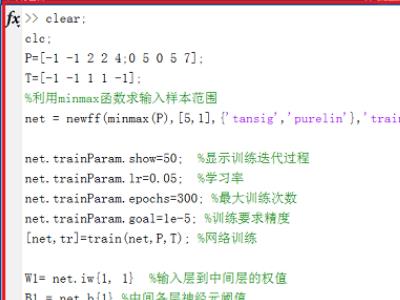
3、在matlab中命令行窗口中定义输入P，输出T，·通过“newff(minmax(P),[5,1]构建BP神经网络，“[net,tr]=train(net,P,T);”进行网络训练，“sim(net,P)”得到仿真预测值。

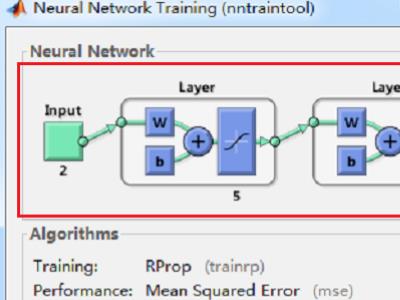
4、在命令行窗口按回车键之后，可以看到出现结果弹窗，最上面的Neural Network下面依次代表的是“输入、隐含层、输出层、输出”，隐含层中有5个神经元。

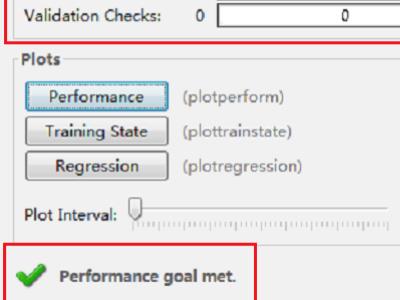
5、Progress下面的Epoch代表迭代次数，Gradient代表梯度，Vaildation Checks代表有效性检查，最后的绿色对勾代表性能目标达成。

6、最后将实际曲线和预测曲线绘制出来，可以看到使用BP神经网络预测的结果曲线基本和实际输出曲线一致。

参考技术A

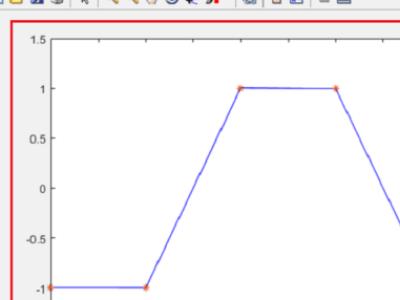
首先需要了解BP神经网络是一种多层前馈网络。以看一下在matlab中BP神经网络的训练函数，有梯度下降法traingd,弹性梯度下降法trainrp，自适应lr梯度下降法traingda等。

因为初始值（初始权值和阀值）都在x这个向量中，x（n，1）的长度n为：n=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum

其中inputnum*hiddennum是输入层到隐含层的权值数量，hiddennum是隐含层神经元个数（即隐含层阀值个数），hiddennum*outputnum是隐含层到输出层权值个数，outputnum是输出层神经元个数（即输出层阀值个数）。

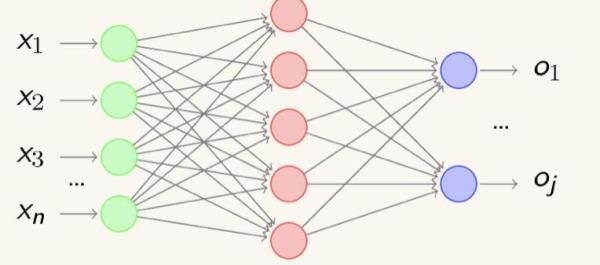
结构

BP网络是在输入层与输出层之间增加若干层(一层或多层)神经元，这些神经元称为隐单元，它们与外界没有直接的联系，但其状态的改变，则能影响输入与输出之间的关系，每一层可以有若干个节点。 

BP神经网络的计算过程由正向计算过程和反向计算过程组成。正向传播过程，输入模式从输入层经隐单元层逐层处理，并转向输出层，每～层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转入反向传播，将误差信号沿原来的连接通路返回，通过修改各神经元的权值，使得误差信号最小。

以上内容参考：百度百科-BP神经网络

参考技术B

这是一个三层神经网络，x里边保存得是你用其他算法确定好的权值和阈值，括号里边计算的是对应各层权值阈值的索引（序号） 。比如 三层神经网络，输入层2  隐含层3 输出层1

w1=x(1:inputnum*hiddennum); 

输入层到隐含层的 权值个数=输入层数量*输出层数 ，你可以想象为输入层 到 隐含层的线，总共2*3 =6个 ，索引值是1-6 ，W1(1,6)

B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);

隐含层的阈值所在索引： 前边到6 了，这个肯定要从6+1开始，间隔就是隐含层阈值的个数3，所以右边范围是6+3.隐含层阈值B1的索引值就是x（7:9）

下边都类似了
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);  隐含层到输出层的权值 x（10，12）
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);  输出层阈值只有一个  x（13,13）

参考技术C 楼主，你是怎么看懂的啊？ 参考技术D 你这是不是用遗传算法优化权值和阀值啊？
我不知道你x的哪里来的？所以也不知道你是如何确定初始权值和阀值。
不过我们平常写程序时这些值都是随机赋予的。追问

就是看不明白，比如说B1中，怎么又有乘法又有加法，而且中间还有冒号？这样B1最后是一个矩阵吗？如果是，它的维数是多少？几行几列？要是这个解释明白了，就把分给你哈。

追答

因为初始值（初始权值和阀值）都在x这个向量中，x（n，1）的长度n为：n=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum
其中inputnum*hiddennum是输入层到隐含层的权值数量，hiddennum是隐含层神经元个数（即隐含层阀值个数），hiddennum*outputnum是隐含层到输出层权值个数，outputnum是输出层神经元个数（即输出层阀值个数）；

本回答被提问者采纳

BP神经网络

 

BP神经网络是一种按误差反向传播的多层前馈神经网络，含有一个或多个隐含层，其拓扑结构与一般神经网络相似，BP神经网络的隐含层激活函数一般是sigmoid函数，输出层如果是函数逼近，其激活函数一般是线性函数，分类问题其激活函数一般是sigmoid函数

BP神经网络的学习一般分为两部分：

一：正向计算各个神经元的输出

二：误差反向传播修正权值和阈值

下面开始BP神经网络的学习算法

以有两个隐含层的BP神经网络为例，下面是其拓扑结构：

规定一些符号：

输入层神经元的个数是M,隐含层1是I，隐含层2是J,输出层是K

输入层的第m个神经元用m表示，同理隐含层1是i，隐含层2是j,输出层是k

输入层到隐含层1的权值连接用W_mi表示，隐含层1到隐含层2用W_ij表示，隐含层2到输出层用W_jk表示

(u,v)分别表示各层的输入和输出

用Ml,Il,Jl,Kl分别标识输入层，隐含层1，隐含层2，输出层

隐含层1第i个神经元的输入：

uⁱ(Il)=∑_{m=1 to M}W_miv^m(ML)

隐含层1第i个神经元的输出：

Vⁱ(Il)=f(uⁱ(Il))

隐含层2第j个神经元的输入：

u^j(Jl)=∑_{i=1 to I}W_ijvⁱ(Il)

隐含层2第j个神经元的输出：

v^j(Jl)=g(u^j(Jl))

输出层的第k个神经元的输入是：

u^k(Kl)=∑_{j=1 to J}W_jkv^j(Jl)

输出层的第k个神经元的输出是：

v^k(Kl)=h(u^k(Kl))

第k个神经元的输出误差是：

e_k=d_k-v^k(Kl)

网络的总误差是：

E=1/2∑_{k=1 to K}(e_k)²

BP学习算法和W-H算法一样是基于梯度下降的学习算法，所以

W(n+1)=W(n)-η∂E/∂W

下面开始求误差反向传播的权值更新：

由链式求导得到：

              ∂E/∂W_jk=(∂E/∂e_k)(∂e_k/∂v^k(Kl))(∂v^k(Kl)/∂u^k(Kl))(∂u^k(Kl)/∂W_jk)

                          =-e_kd(h)v^j(Jl) 其中d(h)表示对h函数求导

故∂E/∂W_jk=-e_kd(h)v^j(Jl)

现在定义局部梯度：

Ψ^k(Kl)=∂E/∂u^k(Kl)

         =(∂E/∂e_k)(∂e_k/∂v^k(Kl))(∂v^k(Kl)/∂u^k(Kl))

         =-e_kd(h)

故∂E/∂W_jk=Ψ^k(Kl)v^j(Jl)

同理得到∂E/∂W_ij=Ψ^j(Jl)vⁱ(Il)

Ψ^j(Jl)=∑_{k=1 to K}W_jkΨ^k(Kl)d(h)d(g)vⁱ(Il)

同理得∂E/W_mi=Ψⁱ(Il)v^m(Ml)

Ψⁱ(Il)=∑_{j=1 to J}W_ijΨ^j(Jl)d(f)v^m(Ml)

由上面叙述，进行权值更新：

w_mi(n+1)=W_mi(n)+η∑_{j=1 to J}W_ijΨ^j(Jl)d(f)v^m(Ml)

W_ij(n+1)=W_ij(n)+η∑_{k=1 to K}W_jkΨ^k(Kl)d(h)d(g)vⁱ(Il)

W_jk(n+1)=W_jk(n)+ηe_kd(h)v^j(Jl)