LeetCode207.课程表 | BFS DFS 邻接表 邻接矩阵
Posted 七夕哒
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode207.课程表 | BFS DFS 邻接表 邻接矩阵相关的知识,希望对你有一定的参考价值。
目录
一、题目
1.1 题目描述
想看优化代码的小伙伴,可以直接看DFS的代码,是最快的,打败了90%。
题目链接如下: LeetCode207
题目截图如下:

1.2 思路分析
直接来说,就是要把先修课学完了,才能学后续的课,数据结构是一个图的形式。
本质上就是看这个图有没有圆存在,有的话,两个课互相指,就不可能学完了。
所以就直接用**图的拓扑排序**解决
拓扑排序,我的理解就是:把一个有向图用序列表示出来,前节点必须在后节点的前面。
二、BFS+邻接矩阵
- 首先记录下图的存储方式,邻接矩阵。
例子如下:

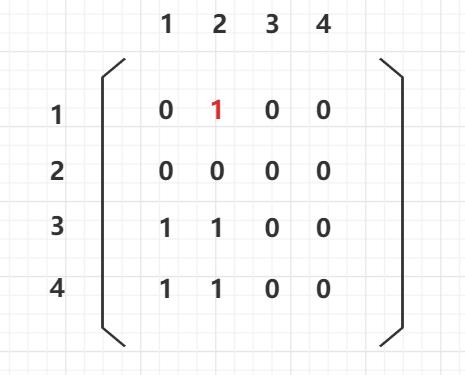
红色的那个1就表示 节点1 指向了 节点2。
这个图的拓扑排序就有很多:
3 4 1 2
4 3 1 2
- 后面思路就很简单了。
- 找到入度为0的所有节点并记录。入度: 前驱节点个数
- 删除这些节点,重新统计入度。
- 重复步骤1和2,直到没有入度为0的节点。
- 计算记录了多少个节点了,如果数量和节点数一样,那就是没问题。如果数量小于节点数量,那就说明成环了。
就和树的BFS一毛一样呀,如果这是一棵树,那完全就是一层一层的统计。
2.1 代码分析
通过分析可以看出来,我们需要以下几个数据结构:
- 二维矩阵matrix[][],用来表示邻接表
- 一维矩阵inDegree[], 用来统计入度
- 堆栈 zeroDegree, 用来做BFS中保存入度为0的节点。
- 已删除节点数 deleteNums, 用来统计删除了多少节点了。
具体操作就是:
将0度节点放入堆栈中,然后遍历堆栈;
调整每个0度节点的邻居的入度,也就是-1。如果邻居为0了,那就加入堆栈;
堆栈遍历完了,就比较数量就完事了。
2.2 完整代码
public boolean canFinish(int numCourses, int[][] prerequisites)
/*
* adjacency List
*/
int[][] matrix=new int[numCourses][numCourses];
/*
* # adjacency List
*/
int[] inDegs=new int[numCourses];
Queue<Integer> zeroDegs=new LinkedList<>();
/*
* generate adjacency List
*/
for(int[] pres:prerequisites)
int pre=pres[1];
int latter=pres[0];
if(matrix[pre][latter]==0)
matrix[pre][latter]=1;
inDegs[latter]++;
/*
* # generate adjacency List
*/
/*
* mark the nodes with 0 in-degrees
*/
for(int i=0;i<inDegs.length;i++)
if(inDegs[i]==0)
zeroDegs.offer(i);
/*
* # mark the nodes with 0 in-degrees (zero-Nodes)
*/
/*
* BFS disadvantage: Each node has to be refreshed for its edge times, time-->O(V+E)
* No break, this algorithm has to run to the end till it gets the topological order. But it's useless in this problem.
* advantage: Can get the topological order.
*/
int deleteNums=0;
while(!zeroDegs.isEmpty())
int deleteCourse=zeroDegs.poll();//get a zero-Nodes
deleteNums++;
/*
* delete the zero-Nodes and refresh its neighbors
*/
for(int i=0;i<numCourses;i++)
if(matrix[deleteCourse][i]!=0)
inDegs[i]--;
if(inDegs[i]==0)
zeroDegs.offer(i);
/*
* # delete the zero-Nodes and refresh its neighbors
*/
return deleteNums==numCourses;
/*
* # BFS
*/
虽然是对的,但是这个结果跑出来很拉跨,效率很低,好像是打败了5%。
然后我就研究了发现用邻接表会好很多。
三、BFS+邻接表
- 首先说下啥是邻接表:
用数组+链表的形式存储邻居节点, 类似HashMap
好处嘛:
- 节省空间,邻接矩阵那么多0呢,白占位置了。
- 查找方便,链表嘛,直接存了邻居节点地址,不用for循环遍历数组去找邻居了。
例子如下:

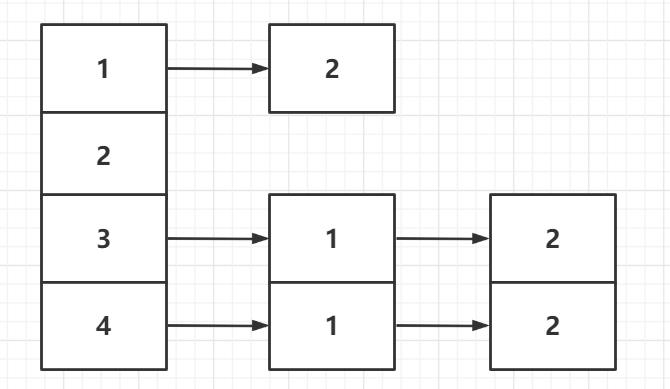
图就不解释了吧,贼清晰。
- 解题思路也是一样的
- 找到入度为0的所有节点并记录。入度: 前驱节点个数
- 删除这些节点,重新统计入度。
- 重复步骤1和2,直到没有入度为0的节点。
- 计算记录了多少个节点了,如果数量和节点数一样,那就是没问题。如果数量小于节点数量,那就说明成环了。
3.1 代码分析
那这次需要用的数据结构是以下这些:
- HashMap<Integer, List> matrix, 用来保存邻接表
- 一维数组 inDegrees[],用来保存入度为0的节点
- 堆栈 zeroDegree, 用来做BFS中保存入度为0的节点。
- 已删除节点数 deleteNums, 用来统计删除了多少节点了。
也就是把保存邻接表的数据结构替换了。
后面其实也一样,就是把相应的数组操作替换为map和链表的操作。
3.2 完整代码
因为我很菜,所以我是把邻接表和邻接矩阵的两种写法放在一起的,方便对比。
大家不想对比的话,就不用管注释。
public boolean canFinish(int numCourses, int[][] prerequisites)
/*
* adjacency List
*/
// int[][] matrix=new int[numCourses][numCourses];
HashMap<Integer, List<Integer>> matrix=new HashMap<Integer, List<Integer>>();
for(int i=0;i<numCourses;i++)
matrix.put(i, new ArrayList<>());
/*
* # adjacency List
*/
int[] inDegs=new int[numCourses];
Queue<Integer> zeroDegs=new LinkedList<>();
/*
* generate adjacency List
*/
// for(int[] pres:prerequisites)
// int pre=pres[1];
// int latter=pres[0];
// if(matrix[pre][latter]==0)
// matrix[pre][latter]=1;
// inDegs[latter]++;
//
//
for(int[] pres:prerequisites)
int pre=pres[1];
int latter=pres[0];
matrix.get(pre).add(latter);
inDegs[latter]++;
/*
* # generate adjacency List
*/
/*
* mark the nodes with 0 in-degrees
*/
for(int i=0;i<inDegs.length;i++)
if(inDegs[i]==0)
zeroDegs.offer(i);
/*
* # mark the nodes with 0 in-degrees (zero-Nodes)
*/
/*
* BFS disadvantage: Every edge of every node has to be calculated, time-->O(V+E)
* And the nodes degree has to be refreshed for several times until it's zero
* No break, this algorithm has to run to the end till it gets the topological order. But it's useless in this problem.
* advantage: Can get the topological order.
*/
int deleteNums=0;
while(!zeroDegs.isEmpty())
int deleteCourse=zeroDegs.poll();//get a zero-Nodes
deleteNums++;
/*
* delete the zero-Nodes and refresh its neighbors
*/
// for(int i=0;i<numCourses;i++)
// if(matrix[deleteCourse][i]!=0)
// inDegs[i]--;
// if(inDegs[i]==0)
// zeroDegs.offer(i);
//
//
//
for(int latter:matrix.get(deleteCourse))
inDegs[latter]--;
if(inDegs[latter]==0)
zeroDegs.offer(latter);
/*
* # delete the zero-Nodes and refresh its neighbors
*/
return deleteNums==numCourses;
/*
* # BFS
*/
替换成邻接表之后表现好了一些,不过还是有点垃圾,忘了数据了,最多提升到打败35%吧,还是不太行。
四、DFS
为啥前面两种表现这么差。
从做题的角度来讲,这是因为计算了一些不需要的东西,比如:拓扑序列。
题目只要判断有没有环,不需要序列。
那就可以换个思路,直接找有没有环就行了,DFS就很好。
4.1 思路分析
从任意一个节点出发,深度优先搜索它的子节点,并且保存搜索路径。
如果有环,那肯定会有路径中的一个节点再次被,直接返回false。
但是如果这个节点,已经被访问过了,但是不在路径中,就不需要DFS它了。因为它被访问是在其他节点的搜索路径中访问的,对当前节点没有影响。而且它本身不成环,访问它也是白费力,已经访问过了,不因为它成环。
所以总的来说,一个节点有两个属性:访问过,在当前路径中。
访问过,用来剪枝。
当前路径,用来判断成环。
4.1 代码分析
代码需要以下数据结构:
- HashMap<Integer, List> matrix, 用来保存邻接表
- 一维数组 visited[],用来记录已经访问过的节点
- 一维数组curPath[],用来记录当前路径中的节点
流程如下:
- 生成邻接表
- 访问每个未访问节点,如果都访问过了,返回true
- 如果当前节点在curPath中,返回false
- 如果不在curPath中,加入curPath。
- 如果还有子节点未访问,访问它的子节点,回到步骤3;如果访问完成,将当前节点从curPath中取消,则回到步骤2。
好像有点绕,但我觉得重点是curPath的操作。就是要及时添加,及时删除。
在访问节点的时候添加,在当前节点及其子节点访问完之后删除。
看代码吧,清晰很多。
4.2 完整代码
public boolean canFinish(int numCourses, int[][] prerequisites)
/*
* adjacency List
*/
HashMap<Integer, List<Integer>> matrix=new HashMap<Integer, List<Integer>>();
for(int i=0;i<numCourses;i++)
matrix.put(i, new ArrayList<>());
/*
* # adjacency List
*/
/*
* generate adjacency List
*/
for(int[] pres:prerequisites)
int pre=pres[1];
int latter=pres[0];
matrix.get(pre).add(latter);
inDegs[latter]++;
/*
* # generate adjacency List
*/
/*
* DFS disadvantage: Can't get the topological order
* advantage: It will stop when found a circle and would go to each edge just once. BFS would check eahc one for several times.
*/
int[] visited=new int[numCourses];
int[] curPath=new int[numCourses];
for(int i=0;i<numCourses;i++)
if(visited[i]==0)
curPath[i]=1;
boolean noCircle=dfs(i,visited,curPath,matrix);
if(!noCircle)
return false;
curPath[i]=0;
return true;
/*
* # DFS
*/
public boolean dfs(int node, int[] visited, int[] curPath, HashMap<Integer, List<Integer>> matrix)
visited[node]=1;
for(int neighbor: matrix.get(node))
if(curPath[neighbor]==1)
return false;
if(visited[neighbor]==0)
curPath[neighbor]=1;
boolean noCircle=dfs(neighbor,visited,curPath, matrix);
if(!noCircle)
return false;
curPath[neighbor]=0;
return true;
我重点研究的是进入dfs,和dfs中的代码。
可以看到,长得类似。
节点加入curPath------->dfs------->节点退出curPath。
但是进入dfs的时候,没有标记节点为已访问,但是标记为了curPath。
- 已访问: 这是因为每个节点要统一操作,子节点的访问不会在外面进入,而是在dfs内部——也就是说dfs内部需要标记节点为已放问,那么在外面就不需要了咯。
- curPath: 这是因为dfs内部,遍历的是所有邻居节点,只添加邻居节点到当前路径中,不包含当前节点。换句话说,要在dfs开始前就将当前节点添加进去。
以上是关于LeetCode207.课程表 | BFS DFS 邻接表 邻接矩阵的主要内容,如果未能解决你的问题,请参考以下文章