《PolyLaneNet：Lane Estimation via Deep Polynomial Regression》论文笔记

Posted 2022-01-27 m_buddy

参考代码：PolyLaneNet

1. 概述

介绍：这篇提出了一种新类型车道线检测算法，它使用多项式表示一条车道线，从而实现对弯曲车道线的适应。总体看文章提出的方法是基于回归的方案，因而比起基于分割、anchor机制的算法能够更快一些，并且没有引入任何先验假设。但是，其对车道线特征的refine上就差一些，导致其相比后序的车道线检测算法存在较大的差距。

2. 方法设计

2.1 整体pipeline

文章提出方法的整体pipeline见下图所示：

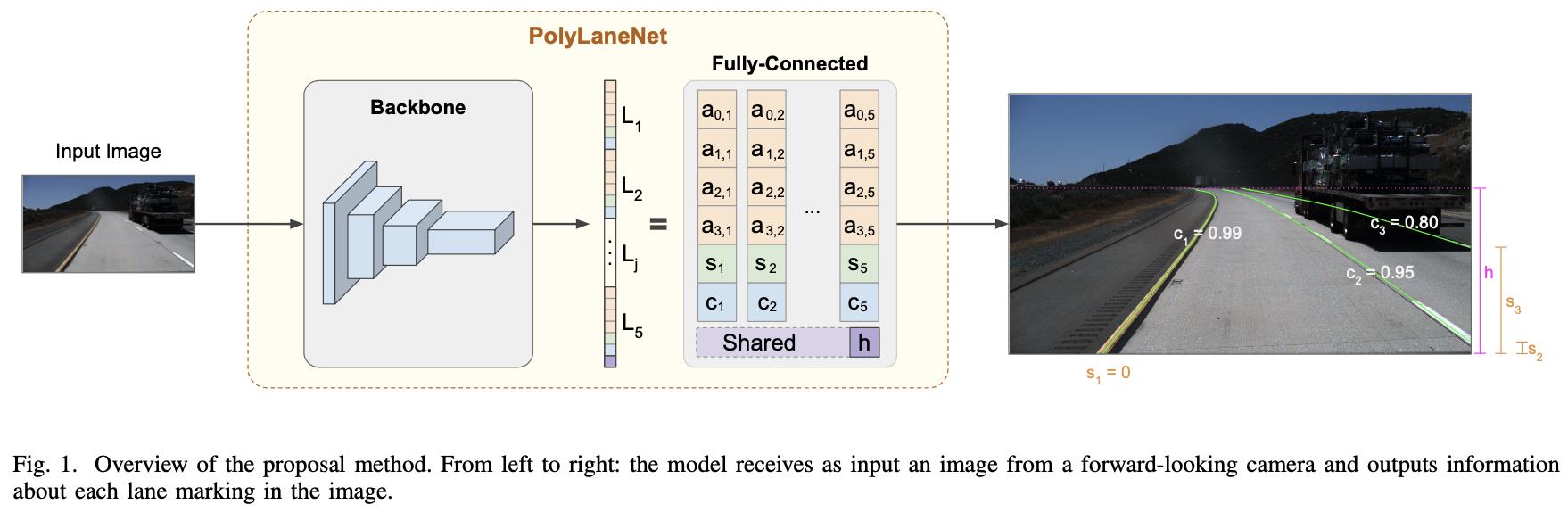
输入的图片经过backbone之后得到高纬度特征，之后经过PolyLanNet（也就是全连接）得到不同车道线的参数。在输入网络进行预测之前需要对车道线的顺序进行排序，也就是从图片的左边开始依次往右编号：

# lib/datasets/lane_dataset.py#L69
old_lanes = sorted(old_lanes, key=lambda x: x[0][0][0])

对于车道线预测的参数维度计算描述为：

parameters:
    num_outputs: 35 # (5 lanes) * (1 conf + 2 (upper & lower) + 4 poly coeffs)

在网络预测出4个对应的多项式参数之后便可以使用多项式表达写出对应车道线的预测值：

# lib/models.py#L135
pred_xs = pred_polys[:, 0] * ys**3 + pred_polys[:, 1] * ys**2 + pred_polys[:, 2] * ys + pred_polys[:, 3]

在损失函数层面，这里的损失函数包含：车道线预测偏移误差（MSELoss）、车道线上下边界误差（MSELoss）、是否为车道线回归误差（CrossEntropyLoss）。则描述为：
$$L(P_j,h,s_j,c_j)={\lambda }_p{L}_p(P_j,L_j^{\ast })+{\lambda }_s\frac{1}{M}\sum _{j=1}{L}_{reg}(s_j,s_j^{\ast })+{\lambda }_c\sum _{j=1}{L}_{cls}(c_j,c_j^{\ast })+{\lambda }_h{L}_{reg}(c_h,c_h^{\ast })$$
TuSimple数据集上的性能表现：

2.2 鲁棒性分析

这部分对车道线检测的鲁棒性进行分析，主要的内容源自：
paper：On Robustness of Lane Detection Models to Physical-World Adversarial Attacks in Autonomous Driving

在该文章中对现有的车道线检测算法进行分类，可以归纳为如下4个类别：

然后使用网络攻击的形式对这些车道线检测算法进行攻击，也就是通过白色/黑色块、线条等手段修改图片内容，再观察这些攻击是否有效，其得到的结果如下表：

在上表中可以看到由于PolyLaneNet采用多项式表达的形式，收到的干扰更少，在相同条件下会显得更加鲁棒。